Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-29T00:08:52.601Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohen-stable families of subsets of integers

Published online by Cambridge University Press:  12 March 2014

Miloš S. Kurilić
Miloš S. Kurilić*
Affiliation:
Institute of Mathematics, University of Novi Sad, Trg Dositeja Obradovića 4, 21000 Novi Sad. Yugoslavia
Get access Rights & Permissions [Opens in a new window]

Abstract

A maximal almost disjoint (mad) family 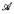⊆ [ω]ω is Cohen-stable if and only if it remains maximal in any Cohen generic extension. Otherwise it is Cohen-unstable. It is shown that a mad family. 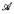.is Cohen-unstable if and only if there is a bijection G from ω to the rationals such that the sets G[A]. A ∈ 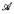are nowhere dense. An ℵ0-mad family, 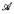. is a mad family with the property that given any countable family ℬ ⊂ [ω]ω such that each element of ℬ meets infinitely many elements of 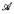in an infinite set there is an element of 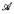meeting each element of ℬ in an infinite set. It is shown that Cohen-stable mad families exist if and only if there exist ℵ0-mad families. Either of the conditions b = c or a < cov(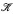) implies that there exist Cohen-stable mad families. Similar results are obtained for splitting families. For example, a splitting family. 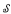. is Cohen-unstable if and only if there is a bijection G from ω to the rationals such that the boundaries of the sets G[S], S ∈ 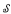are nowhere dense. Also. Cohen-stable splitting families of cardinality ≤ κ exist if and only if ℵ0-splitting families of cardinality ≤ κ exist.

Keywords

Cohen forcingmad familiessplitting families
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 1 , March 2001 , pp. 257 - 270
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Hechler, S. H., Short complete nested sequences in βℕ ∖ ℕ and small almost-disjoint families, General Topology and Applications, vol. 2 (1972), no. 3, pp. 139–149.CrossRefGoogle Scholar
[2]Kamburelis, A. and Wȩglorz, B., Splittings, Archive for Mathematical Logic, vol. 35 (1996), no. 4. pp. 263–277.CrossRefGoogle Scholar
[3]Kunen, K., Set theory, an introduction to independence proofs. North-Holland, Amsterdam, 1980.Google Scholar
[4]Kunen, K., Random and Cohen reals, Handbook of set-theoretic topology (Kunen, K. and Vaughan, J. E., editors). North-Holland, Amsterdam, 1984, pp. 887–911.CrossRefGoogle Scholar
[5]Malyhin, V. I., Topological properties of Cohen generic extensions, Transactions of the Moscow Mathematical Society, vol. 52 (1990), pp. 1–32.Google Scholar
[6]Solovay, R. M., A model of set-theory in which every set of reals is Lebesgue measurable, Annals of Mathematics, vol. 92 (1970). pp. 1–56.CrossRefGoogle Scholar
[7]van Douwen, E. K., The integers and topology, Handbook of set-theoretic topology (Kunen, K. and Vaughan, J. E., editors). North-Holland, Amsterdam, 1984, pp. 111–167.CrossRefGoogle Scholar
[8]Vaughan, J. E., Small uncountable cardinals and topology, Open problems in topology (van Mill, J. and Reed, G. M., editors). North-Holland, Amsterdam, 1990, pp. 195–218.Google Scholar