Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-30T23:53:29.292Z Has data issue: false hasContentIssue false
  • English
  • Français

The classification of small weakly minimal sets. II

Published online by Cambridge University Press:  12 March 2014

Steven Buechler
Steven Buechler*
Affiliation:
Department of Mathematics, University of California, Berkeley, California 94720
*
Department of Mathematics, University of Wisconsin at Milwaukee, Milwaukee, Wisconsin 53201
Get access Rights & Permissions [Opens in a new window]

Abstract

The main result is Vaught's conjecture for weakly minimal, locally modular and non-ω-stable theories. The more general results yielding this are the following.

Theorem A. Suppose that T is a small unidimensional theory and D is a weakly minimal set, definable over the finite set B. Then for all finite A ⊂ D there are only finitely many nonalgebraic strong types over B realized in acl(A) ∩ D.

Theorem B. Suppose that T is a small, unidimensional, non-ω-stable theory such that the universe is weakly minimal and locally modular. Then for all finite A there is a finite B ⊂ cl(A) such that a ∈ cl(A) iff a ∈ cl(b) for some b ∈ B.

Recall the property (S) defined in the abstract of [B1].

Theorem C. Let T be as in Theorem B. Then, if T does not satisfy (S), T has 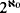many countable models.

Combining Theorem C and the results in [B1] we obtain Vaught's conjecture for such theories.

Type
Survey/expository papers
Information
The Journal of Symbolic Logic , Volume 53 , Issue 2 , June 1988 , pp. 625 - 635
Copyright
Copyright © Association for Symbolic Logic 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B1] Buechler, S., The classification of small weakly minimal sets. I, Classification theory (Chicago, Illinois, 1985), Springer-Verlag, Berlin (to appear).Google Scholar
[B2] Buechler, S., The geometry of weakly minimal types, this Journal, vol. 50 (1985), pp. 1044–1053.Google Scholar
[B3] Buechler, S., “Geometrical” stability theory, Logic Colloquium '85, North-Holland, Amsterdam, 1987, pp. 53–66.Google Scholar
[Hr] Hrushovski, E., Contributions to stable model theory, Ph.D. thesis, University of California, Berkeley, California, 1986.Google Scholar
[L] Loveys, J., Certain weakly minimal theories, Ph.D. thesis, Simon Fraser University, Burnaby, British Columbia, 1986.Google Scholar
[S] Saffe, J., On Vaught's conjecture for superstable theories, preprint, 1982.Google Scholar