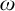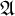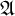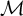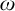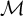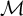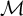1. Introduction
A first-order structure
![]() $\mathfrak {A}$
is called monadically stable iff every expansion of
$\mathfrak {A}$
is called monadically stable iff every expansion of
![]() $\mathfrak {A}$
by unary predicates is stable. We know that this property is also equivalent to a property called tree-decomposability introduced in [Reference Baldwin and Shelah3]. The equivalence follows from the results of [Reference Baldwin and Shelah3] and they are discussed in the introduction in [Reference Lachlan34]. Further equivalent conditions for monadic stability are given in [Reference Lachlan34].
$\mathfrak {A}$
by unary predicates is stable. We know that this property is also equivalent to a property called tree-decomposability introduced in [Reference Baldwin and Shelah3]. The equivalence follows from the results of [Reference Baldwin and Shelah3] and they are discussed in the introduction in [Reference Lachlan34]. Further equivalent conditions for monadic stability are given in [Reference Lachlan34].
In this article we are interested in those monadically stable structures which are
![]() $\omega $
-categorical and countable. We denote the class of these structures by
$\omega $
-categorical and countable. We denote the class of these structures by
![]() $\mathcal {M}$
. Lachlan [Reference Lachlan34] gave a bottom-up description of the class
$\mathcal {M}$
. Lachlan [Reference Lachlan34] gave a bottom-up description of the class
![]() $\mathcal {M}$
in terms of automorphism groups. Namely he showed that a structure is contained in
$\mathcal {M}$
in terms of automorphism groups. Namely he showed that a structure is contained in
![]() $\mathcal {M}$
if and only if its automorphism group can be obtained from finite structures by a finite number of iterations of certain combinatorial constructions, called
$\mathcal {M}$
if and only if its automorphism group can be obtained from finite structures by a finite number of iterations of certain combinatorial constructions, called
![]() $\omega $
-stretches and loose unions. Another interesting characterization of
$\omega $
-stretches and loose unions. Another interesting characterization of
![]() $\mathcal {M}$
is given by Braunfeld [Reference Braunfeld22] in terms of orbit growth on subsets, a countable
$\mathcal {M}$
is given by Braunfeld [Reference Braunfeld22] in terms of orbit growth on subsets, a countable
![]() $\omega $
-categorical structure is monadically stable if and only if it is stable and its orbit growth on subsets is slower than exponential (see Theorem 3.12 for the precise formulation).
$\omega $
-categorical structure is monadically stable if and only if it is stable and its orbit growth on subsets is slower than exponential (see Theorem 3.12 for the precise formulation).
In the present article we refine the description of automorphism groups of structures in
![]() $\mathcal {M}$
given in [Reference Lachlan34] (Section 3). We define recursively a sequence of classes of permutation groups
$\mathcal {M}$
given in [Reference Lachlan34] (Section 3). We define recursively a sequence of classes of permutation groups
![]() $\mathcal {H}_n'\colon n\in \omega $
such that
$\mathcal {H}_n'\colon n\in \omega $
such that
![]() $\mathcal {H}_n'$
is exactly the class of automorphism groups of those structures in
$\mathcal {H}_n'$
is exactly the class of automorphism groups of those structures in
![]() $\mathcal {M}$
whose Morley rank are at most n. We know from the results of [Reference Lachlan34] that every monadically stable structure has finite Morley rank. This implies the following.
$\mathcal {M}$
whose Morley rank are at most n. We know from the results of [Reference Lachlan34] that every monadically stable structure has finite Morley rank. This implies the following.
Theorem 1.1. A countable structure
![]() $\mathfrak {A}$
is monadically stable if and only if
$\mathfrak {A}$
is monadically stable if and only if
![]() $\operatorname {Aut}(\mathfrak {A})\in \mathcal {H}':=\bigcup _{n=0}^\infty \mathcal {H}_n'$
.
$\operatorname {Aut}(\mathfrak {A})\in \mathcal {H}':=\bigcup _{n=0}^\infty \mathcal {H}_n'$
.
The main difference between our description and the one given in [Reference Lachlan34] is that in our description the groups in
![]() $\mathcal {H}_n'$
have an explicit definition using the groups in
$\mathcal {H}_n'$
have an explicit definition using the groups in
![]() $\mathcal {H}_{n-1}'$
.
$\mathcal {H}_{n-1}'$
.
We also show that
![]() $\mathcal {H}'$
is the smallest class of permutation groups which contains all finite domain permutation groups, is closed under isomorphism, and is closed under taking finite direct products, wreath products with
$\mathcal {H}'$
is the smallest class of permutation groups which contains all finite domain permutation groups, is closed under isomorphism, and is closed under taking finite direct products, wreath products with
![]() $\operatorname {Sym}(\omega )$
, and finite index supergroups. This result also gives rise to a rather simple description of the class
$\operatorname {Sym}(\omega )$
, and finite index supergroups. This result also gives rise to a rather simple description of the class
![]() $\mathcal {M}$
without any mention of automorphism groups.
$\mathcal {M}$
without any mention of automorphism groups.
Theorem 1.2.
![]() $\mathcal {M}$
is the smallest class of structures which contains the one-element pure set, is closed under isomorphism, and is closed under taking finite disjoint unions, infinite copies, and finite index first-order reducts.
$\mathcal {M}$
is the smallest class of structures which contains the one-element pure set, is closed under isomorphism, and is closed under taking finite disjoint unions, infinite copies, and finite index first-order reducts.
1.1. Finite homogenizability and finite boundedness
A structure
![]() $\mathfrak {A}$
is called homogeneous if every homomorphism between finitely generated substructures of
$\mathfrak {A}$
is called homogeneous if every homomorphism between finitely generated substructures of
![]() $\mathfrak {A}$
can be extended to an automorphism of
$\mathfrak {A}$
can be extended to an automorphism of
![]() $\mathfrak {A}$
. A structure is called finitely homogenizable if it is first-order interdefinable with a homogeneous structure with a finite relational signature. In [Reference Lachlan34] Lachlan showed that all structures in
$\mathfrak {A}$
. A structure is called finitely homogenizable if it is first-order interdefinable with a homogeneous structure with a finite relational signature. In [Reference Lachlan34] Lachlan showed that all structures in
![]() $\mathcal {M}$
are finitely homogenizable.
$\mathcal {M}$
are finitely homogenizable.
In the study of finitely homogeneous structures we are particularly interested in the ones which are finitely bounded, i.e., the ones whose finite substructures can be described by finitely many forbidden substructures. The precise definition can be found in Section 2.7. Lachlan [Reference Lachlan34] showed that every
![]() $\omega $
-categorical monadically stable structure is finitely homogenizable. On the other hand, by the results of [Reference Knight and Lachlan32] we know that every stable homogeneous structure is finitely bounded. This implies that every structure in
$\omega $
-categorical monadically stable structure is finitely homogenizable. On the other hand, by the results of [Reference Knight and Lachlan32] we know that every stable homogeneous structure is finitely bounded. This implies that every structure in
![]() $\mathcal {M}$
is first-order interdefinable with a finitely bounded homogeneous structure (Theorem 4.9). In Section 4 we give a direct and more elementary proof of this statement using our classification.
$\mathcal {M}$
is first-order interdefinable with a finitely bounded homogeneous structure (Theorem 4.9). In Section 4 we give a direct and more elementary proof of this statement using our classification.
1.2. Connection to CSPs
Let
![]() $\mathfrak {B}$
be a structure with a finite relational signature. Then the Constraint Satisfaction Problem (CSP) over
$\mathfrak {B}$
be a structure with a finite relational signature. Then the Constraint Satisfaction Problem (CSP) over
![]() $\mathfrak {B}$
, denoted by
$\mathfrak {B}$
, denoted by
![]() $\operatorname {CSP}(\mathfrak {B})$
, is the computational problem of deciding whether a given finite structure
$\operatorname {CSP}(\mathfrak {B})$
, is the computational problem of deciding whether a given finite structure
![]() $\mathfrak {A}$
with the same signature as
$\mathfrak {A}$
with the same signature as
![]() $\mathfrak {B}$
has a homomorphism to
$\mathfrak {B}$
has a homomorphism to
![]() $\mathfrak {B}$
. Using concepts and techniques from universal algebra, Bulatov and Zhuk proved that for finite structures
$\mathfrak {B}$
. Using concepts and techniques from universal algebra, Bulatov and Zhuk proved that for finite structures
![]() $\mathfrak {B}$
the computational complexity of
$\mathfrak {B}$
the computational complexity of
![]() $\operatorname {CSP}(\mathfrak {B})$
satisfies a dichotomy: it is either in
$\operatorname {CSP}(\mathfrak {B})$
satisfies a dichotomy: it is either in
![]() $\mathbf {P}$
or it is
$\mathbf {P}$
or it is
![]() $\mathbf {NP}$
-complete [Reference Bulatov24, Reference Zhuk39]. The universal algebraic approach for CSPs can also be generalized for countable
$\mathbf {NP}$
-complete [Reference Bulatov24, Reference Zhuk39]. The universal algebraic approach for CSPs can also be generalized for countable
![]() $\omega $
-categorical structures. However as opposed to the finite domain case one cannot expect such a CSP dichotomy for
$\omega $
-categorical structures. However as opposed to the finite domain case one cannot expect such a CSP dichotomy for
![]() $\omega $
-categorical structures since in general we do not even know whether
$\omega $
-categorical structures since in general we do not even know whether
![]() $\operatorname {CSP}(\mathfrak {B})$
is in
$\operatorname {CSP}(\mathfrak {B})$
is in
![]() $\mathbf {NP}$
. In fact we know that
$\mathbf {NP}$
. In fact we know that
![]() $\operatorname {CSP}(\mathfrak {B})$
may be undecidable even for homogeneous structures with a finite relational signature (see for instance [Reference Bodirsky and Nešetřil17]). One way to guarantee that
$\operatorname {CSP}(\mathfrak {B})$
may be undecidable even for homogeneous structures with a finite relational signature (see for instance [Reference Bodirsky and Nešetřil17]). One way to guarantee that
![]() $\operatorname {CSP}(\mathfrak {B})$
is at least in
$\operatorname {CSP}(\mathfrak {B})$
is at least in
![]() $\mathbf {NP}$
is to assume that
$\mathbf {NP}$
is to assume that
![]() $\mathfrak {B}$
is homogeneous and finitely bounded, or a reduct of such a structure. This motivates the following complexity dichotomy conjecture, originally presented in [Reference Bodirsky, Pinsker and Pongrácz20].
$\mathfrak {B}$
is homogeneous and finitely bounded, or a reduct of such a structure. This motivates the following complexity dichotomy conjecture, originally presented in [Reference Bodirsky, Pinsker and Pongrácz20].
Conjecture 1.3 (Infinite domain CSP dichotomy conjecture)
Let
![]() $\mathfrak {A}$
be a countable finitely bounded homogeneous structure, and let
$\mathfrak {A}$
be a countable finitely bounded homogeneous structure, and let
![]() $\mathfrak {B}$
be a first-order reduct of
$\mathfrak {B}$
be a first-order reduct of
![]() $\mathfrak {A}$
with a finite relational signature. Then the
$\mathfrak {A}$
with a finite relational signature. Then the
![]() $\operatorname {CSP}(\mathfrak {B})$
is either in
$\operatorname {CSP}(\mathfrak {B})$
is either in
![]() $\mathbf {P}$
or it is
$\mathbf {P}$
or it is
![]() $\mathbf {NP}$
-complete.
$\mathbf {NP}$
-complete.
The conjecture above has been solved for many classes of structures, such as the first-order reducts of:
-
• the pure set
 $(\mathbb {N};=)$
[Reference Bodirsky and Kára14],
$(\mathbb {N};=)$
[Reference Bodirsky and Kára14], -
• the universal linear order
 $(\mathbb {Q};<)$
[Reference Bodirsky and Kára15],
$(\mathbb {Q};<)$
[Reference Bodirsky and Kára15], -
• the random graph [Reference Bodirsky and Pinsker18],
-
• the random poset [Reference Kompatscher and Van Pham33],
-
• unary
 $\omega $
-categorical structures [Reference Bodirsky and Mottet16],
$\omega $
-categorical structures [Reference Bodirsky and Mottet16],
and all expansions of the homogeneous RCC5-structure by first-order definable relations [Reference Bodirsky and Bodor10]. (RCC5-structures arise in the formalism of spatial reasoning, introduced in [Reference Bennett5].)
Theorem 4.9 implies that all structures in
![]() $\mathcal {M}$
fall into the scope of the conjecture above. We mention one more property of the class
$\mathcal {M}$
fall into the scope of the conjecture above. We mention one more property of the class
![]() $\mathcal {M}$
which makes it a good candidate for a CSP dichotomy result, namely that it is closed under taking model-complete cores. A countable
$\mathcal {M}$
which makes it a good candidate for a CSP dichotomy result, namely that it is closed under taking model-complete cores. A countable
![]() $\omega $
-categorical structure is called a model-complete core if the closure of its automorphism group is the same as its endomorphism monoid. Two structures are called homomorphically equivalent if there exist homomorphisms between them in both directions. Clearly, if two structures are homomorphically equivalent then they have the same CSP. We know that every
$\omega $
-categorical structure is called a model-complete core if the closure of its automorphism group is the same as its endomorphism monoid. Two structures are called homomorphically equivalent if there exist homomorphisms between them in both directions. Clearly, if two structures are homomorphically equivalent then they have the same CSP. We know that every
![]() $\omega $
-categorical structure
$\omega $
-categorical structure
![]() $\mathfrak {B}$
is homomorphically equivalent to an (up to isomorphism unique) model-complete core
$\mathfrak {B}$
is homomorphically equivalent to an (up to isomorphism unique) model-complete core
![]() $\mathfrak {C}$
[Reference Bodirsky6]. Moreover the structure
$\mathfrak {C}$
[Reference Bodirsky6]. Moreover the structure
![]() $\mathfrak {C}$
is also
$\mathfrak {C}$
is also
![]() $\omega $
-categorical, and it is called the model-complete core of
$\omega $
-categorical, and it is called the model-complete core of
![]() $\mathfrak {B}$
. As we argued above, every countable
$\mathfrak {B}$
. As we argued above, every countable
![]() $\omega $
-categorical structures has the same CSP as its model-complete core. Moreover some of the universal algebraic techniques only work under the assumption that the domain structure is a model-complete core. Thus in the analysis of CSPs we usually prefer to work with the model-complete cores of structures. This reduction is a key step in the solution of all the dichotomy results mentioned above. For this reason when formulating a CSP dichotomy for a class
$\omega $
-categorical structures has the same CSP as its model-complete core. Moreover some of the universal algebraic techniques only work under the assumption that the domain structure is a model-complete core. Thus in the analysis of CSPs we usually prefer to work with the model-complete cores of structures. This reduction is a key step in the solution of all the dichotomy results mentioned above. For this reason when formulating a CSP dichotomy for a class
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\omega $
-categorical structures it is useful to have a class
$\omega $
-categorical structures it is useful to have a class
![]() $\mathcal {C}$
which is closed under taking model-complete cores. This property is satisfied by
$\mathcal {C}$
which is closed under taking model-complete cores. This property is satisfied by
![]() $\mathcal {M}$
for simple orbit growth reasons (see Section 3).
$\mathcal {M}$
for simple orbit growth reasons (see Section 3).
For more details on infinite domain CSPs we refer the reader to [Reference Barto and Pinsker4], [Reference Bodirsky7], or [Reference Bodirsky9].
1.3. Thomas’ conjecture
In [Reference Thomas37] Thomas made the conjecture that a countable homogeneous structure over a finite relational signature has only finitely many reducts up to first-order interdefinability. The conjecture has been verified for many well-known homogeneous structures. The list includes the rationals with the usual ordering [Reference Cameron25], the countably infinite random graph [Reference Thomas37], the homogeneous universal
![]() $K_n$
-free graphs [Reference Thomas38], the expansion of
$K_n$
-free graphs [Reference Thomas38], the expansion of
![]() $({\mathbb Q};<)$
by a constant [Reference Junker and Ziegler31], the universal homogeneous partial order [Reference Pach, Pinsker, Pluhár, Pongrácz and Szabó35], the random ordered graph [Reference Bodirsky, Pinsker and Pongrácz19], and many more [Reference Agarwal1, Reference Agarwal and Kompatscher2, Reference Bodirsky, Bradley-Williams, Pinsker and Pongrácz12, Reference Bodirsky, Jonsson and Van Pham13]. Note that if we drop the assumption that the signature of the homogeneous structure
$({\mathbb Q};<)$
by a constant [Reference Junker and Ziegler31], the universal homogeneous partial order [Reference Pach, Pinsker, Pluhár, Pongrácz and Szabó35], the random ordered graph [Reference Bodirsky, Pinsker and Pongrácz19], and many more [Reference Agarwal1, Reference Agarwal and Kompatscher2, Reference Bodirsky, Bradley-Williams, Pinsker and Pongrácz12, Reference Bodirsky, Jonsson and Van Pham13]. Note that if we drop the assumption that the signature of the homogeneous structure
![]() $\mathfrak {A}$
is relational, then Thomas’ conjecture is false even if we keep the assumption that
$\mathfrak {A}$
is relational, then Thomas’ conjecture is false even if we keep the assumption that
![]() $\mathfrak {A}$
is
$\mathfrak {A}$
is
![]() $\omega $
-categorical: already the countable atomless Boolean algebra has infinitely many first-order reducts [Reference Bodor, Cameron and Szabó21].
$\omega $
-categorical: already the countable atomless Boolean algebra has infinitely many first-order reducts [Reference Bodor, Cameron and Szabó21].
Even though Thomas’ conjecture has been verified for several individual structures, there does not seem to be much progress towards proving it in its full generality. In a recent paper [Reference Bodirsky and Bodor11] the authors showed that Thomas’ conjecture holds for all cellular structures. In this article we further generalize this result by showing that Thomas’ conjecture also holds for the entire class
![]() $\mathcal {M}$
(Theorem 5.11). Finally, we mention a recent result by Simon [Reference Simon36] where he showed that Thomas’ conjecture holds for another robust class of structures, namely the class of
$\mathcal {M}$
(Theorem 5.11). Finally, we mention a recent result by Simon [Reference Simon36] where he showed that Thomas’ conjecture holds for another robust class of structures, namely the class of
![]() $\omega $
-categorical primitive NIP structures with thorn rank 1. This class contains for instance all the generalized random permutation i.e., the Fraïssé limit
$\omega $
-categorical primitive NIP structures with thorn rank 1. This class contains for instance all the generalized random permutation i.e., the Fraïssé limit
![]() $(M;<_1,\dots ,<_n)$
of all finite structures equipped with n linear orders.
$(M;<_1,\dots ,<_n)$
of all finite structures equipped with n linear orders.
2. Preliminaries
2.1. Permutation groups
For a group G we write
![]() $H\leq G$
if H is a subgroup of G and
$H\leq G$
if H is a subgroup of G and
![]() $H\triangleleft G$
if H is a normal subgroup of G. If
$H\triangleleft G$
if H is a normal subgroup of G. If
![]() $H\leq G$
then we write
$H\leq G$
then we write
![]() $|G:H|$
for the index of H in G. For a set X we write
$|G:H|$
for the index of H in G. For a set X we write
![]() $\operatorname {id}(X)$
for the identity map on X. Sometimes we drop the set X from the notation if it is clear from the context.
$\operatorname {id}(X)$
for the identity map on X. Sometimes we drop the set X from the notation if it is clear from the context.
We say that a group G is a permutation group if G is a subgroup of
![]() $\operatorname {Sym}(X)$
for some X. Note that whenever G is a permutation group then the set X witnessing this fact is unique (it is the domain of the identity element). We call this set the domain of G, and we denote it by
$\operatorname {Sym}(X)$
for some X. Note that whenever G is a permutation group then the set X witnessing this fact is unique (it is the domain of the identity element). We call this set the domain of G, and we denote it by
![]() $\operatorname {Dom}(G)$
.
$\operatorname {Dom}(G)$
.
If
![]() $G\subset \operatorname {Sym}(X)$
is a permutation group, and
$G\subset \operatorname {Sym}(X)$
is a permutation group, and
![]() $e\colon X\to Y$
is any injective function, then the map defined as
$e\colon X\to Y$
is any injective function, then the map defined as
![]() $\iota (e)\colon \gamma \mapsto e\gamma e^{-1}$
is a homomorphism from G to
$\iota (e)\colon \gamma \mapsto e\gamma e^{-1}$
is a homomorphism from G to
![]() $\operatorname {Sym}(e(X))$
, and is referred to as the homomorphism induced by e.
$\operatorname {Sym}(e(X))$
, and is referred to as the homomorphism induced by e.
Two permutation groups G and H are called isomorphic as permutation groups if there is a bijection
![]() $e\colon \operatorname {Dom}(G)\rightarrow \operatorname {Dom}(H)$
such that the homomorphism
$e\colon \operatorname {Dom}(G)\rightarrow \operatorname {Dom}(H)$
such that the homomorphism
![]() $\iota (e)$
induced by e is an isomorphism between G and H. Note that this condition is strictly stronger than saying that G and H are isomorphic as groups. For instance the trivial permutation groups
$\iota (e)$
induced by e is an isomorphism between G and H. Note that this condition is strictly stronger than saying that G and H are isomorphic as groups. For instance the trivial permutation groups
![]() $\{\operatorname {id}(X)\}$
are isomorphic for every set X as groups, but
$\{\operatorname {id}(X)\}$
are isomorphic for every set X as groups, but
![]() $\{\operatorname {id}(X)\}$
and
$\{\operatorname {id}(X)\}$
and
![]() $\{\operatorname {id}(Y)\}$
are isomorphic as permutation groups only if
$\{\operatorname {id}(Y)\}$
are isomorphic as permutation groups only if
![]() $|X|=|Y|$
. All the groups in this article will be permutation groups, and when we say that two permutation groups are isomorphic we always mean that they are isomorphic as permutation groups.
$|X|=|Y|$
. All the groups in this article will be permutation groups, and when we say that two permutation groups are isomorphic we always mean that they are isomorphic as permutation groups.
Assume that G is a permutation group, and
![]() $Y\subset \operatorname {Dom}(G)$
. Then we use the following notation.
$Y\subset \operatorname {Dom}(G)$
. Then we use the following notation.
-
•
 $G_{Y}$
denotes the pointwise stabilizer of Y, that is,
$G_{Y}$
denotes the pointwise stabilizer of Y, that is,
 $G_Y=\{g\in G\colon \forall y\in Y(g(y)=y)\}$
.
$G_Y=\{g\in G\colon \forall y\in Y(g(y)=y)\}$
. -
•
 $G_{\{Y\}}$
denotes the setwise stabilizer of Y, that is,
$G_{\{Y\}}$
denotes the setwise stabilizer of Y, that is,
 $G_{\{Y\}}=\{g\in G\colon \forall y\in Y(g(y)\in Y)\}$
.
$G_{\{Y\}}=\{g\in G\colon \forall y\in Y(g(y)\in Y)\}$
. -
•
 $G|_Y$
denotes the restriction of G to Y, that is,
$G|_Y$
denotes the restriction of G to Y, that is,
 $G|_Y=\{h|_Y\colon h\in G\}$
, provided that Y is invariant under G.
$G|_Y=\{h|_Y\colon h\in G\}$
, provided that Y is invariant under G. -
•
 $G_{(Y)}:=G_{\{Y\}}|_Y=G_{\{\operatorname {Dom}(G)\setminus Y\}}|_Y$
.
$G_{(Y)}:=G_{\{Y\}}|_Y=G_{\{\operatorname {Dom}(G)\setminus Y\}}|_Y$
. -
•
 $G_{((Y))}:=G_{\operatorname {Dom}(G)\setminus Y}|_Y$
.
$G_{((Y))}:=G_{\operatorname {Dom}(G)\setminus Y}|_Y$
.
Whenever the set Y is finite, say
![]() $Y=\{y_1,\dots ,y_n\}$
, we simply write
$Y=\{y_1,\dots ,y_n\}$
, we simply write
![]() $G_{y_1,\dots ,y_n}$
for
$G_{y_1,\dots ,y_n}$
for
![]() $G_Y$
.
$G_Y$
.
If E is an equivalence relation defined on a set X then we denote by
![]() $X/E$
the quotient set of X with respect to E, and for any
$X/E$
the quotient set of X with respect to E, and for any
![]() $x\in X$
we write
$x\in X$
we write
![]() $[x]_E$
for its equivalence class with respect to E. Then by definition
$[x]_E$
for its equivalence class with respect to E. Then by definition
![]() $(x,y)\in E$
iff
$(x,y)\in E$
iff
![]() $[x]_E=[y]_E$
. An equivalence relation E defined on
$[x]_E=[y]_E$
. An equivalence relation E defined on
![]() $\operatorname {Dom}(G)$
for some permutation group G is called a congruence of G if and only if E is preserved by every permutation in G. In this case there is a natural map
$\operatorname {Dom}(G)$
for some permutation group G is called a congruence of G if and only if E is preserved by every permutation in G. In this case there is a natural map
![]() $G\to \operatorname {Sym}(\operatorname {Dom}(G)/E)$
that maps
$G\to \operatorname {Sym}(\operatorname {Dom}(G)/E)$
that maps
![]() $g\mapsto g/E$
, where
$g\mapsto g/E$
, where
![]() $g/E([x]_E)=[g(x)]_E$
. We define
$g/E([x]_E)=[g(x)]_E$
. We define
![]() $G/E$
as
$G/E$
as
![]() $\{g/E\colon g\in G\}$
.
$\{g/E\colon g\in G\}$
.
2.2. Topology
Every permutation group is naturally equipped with a topology, called the topology of pointwise convergence. This topology can be defined as the subspace topology of the product space
![]() ${}^XX$
where X is equipped with the discrete topology. A sequence
${}^XX$
where X is equipped with the discrete topology. A sequence
![]() $(g_n)_n$
in G converges to a permutation
$(g_n)_n$
in G converges to a permutation
![]() $g\in \operatorname {Sym}(X)$
with respect to this topology if and only if for all finite subsets F of X there exists an n such that
$g\in \operatorname {Sym}(X)$
with respect to this topology if and only if for all finite subsets F of X there exists an n such that
![]() $g_i|_F=g|_F$
for all
$g_i|_F=g|_F$
for all
![]() $i\geq n$
.
$i\geq n$
.
We say that a permutation group
![]() $G\leq \operatorname {Sym}(X)$
is closed if it is closed in the topology of pointwise convergence. Equivalently,
$G\leq \operatorname {Sym}(X)$
is closed if it is closed in the topology of pointwise convergence. Equivalently,
![]() $G\leq \operatorname {Sym}(X)$
is closed if and only if it satisfies the following property: for all
$G\leq \operatorname {Sym}(X)$
is closed if and only if it satisfies the following property: for all
![]() $g\in \operatorname {Sym}(X)$
, if for every finite
$g\in \operatorname {Sym}(X)$
, if for every finite
![]() $F\subset X$
there exists
$F\subset X$
there exists
![]() $g'\in G$
such that
$g'\in G$
such that
![]() $g'|F=g|F$
then
$g'|F=g|F$
then
![]() $g\in G$
.
$g\in G$
.
2.3. Orbit growth functions, oligomorphic groups
There are three natural sequences counting orbits attached to a permutation group introduced and discussed in general in [Reference Cameron26, Reference Cameron27].
Definition 2.1. Let
![]() $G\leq \operatorname {Sym}(X)$
be a permutation group, and let n be a positive integer. Then:
$G\leq \operatorname {Sym}(X)$
be a permutation group, and let n be a positive integer. Then:
-
•
 $o_n(G)$
denotes the number of n-orbits of G, i.e., the number of orbits of the natural action
$o_n(G)$
denotes the number of n-orbits of G, i.e., the number of orbits of the natural action
 $G\curvearrowright X^n$
.
$G\curvearrowright X^n$
. -
•
 $o^s_n(G)$
denotes the number of orbits of n-subsets of G, i.e., the number of orbits of the natural action
$o^s_n(G)$
denotes the number of orbits of n-subsets of G, i.e., the number of orbits of the natural action
 $G\curvearrowright {X\choose n}=\{Y\subset X\colon |Y|=n \}$
.
$G\curvearrowright {X\choose n}=\{Y\subset X\colon |Y|=n \}$
.
A permutation group is called oligomorphic if and only if
![]() $o_n(G)$
is finite for all n.
$o_n(G)$
is finite for all n.
Remark 2.2. It follows easily from the definitions that for any permutation group G the following inequalities hold:
![]() $o^s_n(G)\leq o^i_n(G)\leq o_n(G)\leq n!o^s_n(G)$
. Therefore the following are equivalent:
$o^s_n(G)\leq o^i_n(G)\leq o_n(G)\leq n!o^s_n(G)$
. Therefore the following are equivalent:
-
• G is oligomorphic.
-
•
 $o^i_n(G)$
is finite for all n.
$o^i_n(G)$
is finite for all n. -
•
 $o^s_n(G)$
is finite for all n.
$o^s_n(G)$
is finite for all n.
We often use the following easy observation.
Observation 2.3. If
![]() $G\leq H$
are permutation groups, then
$G\leq H$
are permutation groups, then
![]() $f_n(H)\leq f_n(G)$
where f is any of the operators
$f_n(H)\leq f_n(G)$
where f is any of the operators
![]() $o,o^i$
, or
$o,o^i$
, or
![]() $o^s$
. In particular every group containing an oligomorphic group is oligomorphic.
$o^s$
. In particular every group containing an oligomorphic group is oligomorphic.
2.4. Direct products
Let
![]() $\{X_i\colon i\in I\}$
be a set of pairwise disjoint sets, and for each
$\{X_i\colon i\in I\}$
be a set of pairwise disjoint sets, and for each
![]() $i\in I$
let
$i\in I$
let
![]() $G_i$
be a permutation group acting on
$G_i$
be a permutation group acting on
![]() $X_i$
. Then we define the direct product of the permutation groups
$X_i$
. Then we define the direct product of the permutation groups
![]() $G_i$
, denoted by
$G_i$
, denoted by
![]() $\prod _{i\in I}G_i$
, to be the set of all permutations of
$\prod _{i\in I}G_i$
, to be the set of all permutations of
![]() $X:=\bigcup \{X_i\colon i\in I\}$
which can be written as
$X:=\bigcup \{X_i\colon i\in I\}$
which can be written as
![]() $\bigcup \{f(i)\colon i\in I\}$
, for some
$\bigcup \{f(i)\colon i\in I\}$
, for some
![]() $f\colon I\to \prod _{i\in I}G_i$
that satisfies
$f\colon I\to \prod _{i\in I}G_i$
that satisfies
![]() $f(i)\in G_i$
for all
$f(i)\in G_i$
for all
![]() $i\in I$
. Then
$i\in I$
. Then
![]() $\prod _{i\in I}G_i$
as a group is also the usual direct product of the groups
$\prod _{i\in I}G_i$
as a group is also the usual direct product of the groups
![]() $G_i\colon i\in I$
.
$G_i\colon i\in I$
.
Let
![]() $G\leq \operatorname {Sym}(X)$
be a permutation group and let I be any set. Then we define the power
$G\leq \operatorname {Sym}(X)$
be a permutation group and let I be any set. Then we define the power
![]() $G^I$
to be
$G^I$
to be
![]() $\prod _{i\in I}G_s$
, where
$\prod _{i\in I}G_s$
, where
![]() $G_i:=\{(g,i)\colon g\in G\}$
and
$G_i:=\{(g,i)\colon g\in G\}$
and
![]() $(g,i)(g',i)=(gg',i)$
. This makes sense since the sets
$(g,i)(g',i)=(gg',i)$
. This makes sense since the sets
![]() $\operatorname {Dom}(G_i)=X\times \{i\}: i\in I$
are pairwise disjoint. Then
$\operatorname {Dom}(G_i)=X\times \{i\}: i\in I$
are pairwise disjoint. Then
![]() $\operatorname {Dom}(G^I)=X\times I$
, and since all
$\operatorname {Dom}(G^I)=X\times I$
, and since all
![]() $G_i$
are isomorphic to G it follows that
$G_i$
are isomorphic to G it follows that
![]() $G^I$
is isomorphic to the power
$G^I$
is isomorphic to the power
![]() $G^{|I|}$
as a group.
$G^{|I|}$
as a group.
It follows easily from the definition that any direct product of closed groups is again closed. This also means that any power of a closed group is closed.
It is easy to see that every n-orbit of a direct product
![]() $G:=\prod _{i\in I}G_i$
can be written as the union of
$G:=\prod _{i\in I}G_i$
can be written as the union of
![]() $n_i$
-orbits of
$n_i$
-orbits of
![]() $G_i$
for some sequence of natural numbers
$G_i$
for some sequence of natural numbers
![]() $(n_i)_{i\in I}$
with
$(n_i)_{i\in I}$
with
![]() $\sum _{i\in I}n_i=n$
. This implies that if I is finite then the number of n-orbits of G is at most
$\sum _{i\in I}n_i=n$
. This implies that if I is finite then the number of n-orbits of G is at most
![]() ${|I| \choose n}M^n$
where M is the maximum of
${|I| \choose n}M^n$
where M is the maximum of
![]() $o_n(G_i)$
with
$o_n(G_i)$
with
![]() $i\in I$
. In particular if
$i\in I$
. In particular if
![]() $o_n(G_i)$
is finite for all
$o_n(G_i)$
is finite for all
![]() $i\in I$
and I is finite then
$i\in I$
and I is finite then
![]() $o_n(G)$
is also finite. Thus any finite direct product of oligomorphic groups is again oligomorphic.
$o_n(G)$
is also finite. Thus any finite direct product of oligomorphic groups is again oligomorphic.
2.5. Wreath products
Let
![]() $G\leq \operatorname {Sym}(X)$
and
$G\leq \operatorname {Sym}(X)$
and
![]() $H\leq \operatorname {Sym}(Y)$
be permutation groups. Then we define the wreath product of the groups G and H, denoted by
$H\leq \operatorname {Sym}(Y)$
be permutation groups. Then we define the wreath product of the groups G and H, denoted by
![]() $G\wr H$
, as follows. The domain set of
$G\wr H$
, as follows. The domain set of
![]() $G\wr H$
is
$G\wr H$
is
![]() $X\times Y$
and a permutation
$X\times Y$
and a permutation
![]() $\sigma \in \operatorname {Sym}(X\times Y)$
is contained in
$\sigma \in \operatorname {Sym}(X\times Y)$
is contained in
![]() $G\wr H$
if and only if there exist
$G\wr H$
if and only if there exist
![]() $\beta \in H$
and, for all
$\beta \in H$
and, for all
![]() $y\in Y$
,
$y\in Y$
,
![]() $\alpha _y\in G$
such that, for all
$\alpha _y\in G$
such that, for all
![]() $x\in X$
and
$x\in X$
and
![]() $y\in Y$
we have
$y\in Y$
we have
![]() $\sigma (x,y)=(\alpha _y(x),\beta (y))$
. Note that
$\sigma (x,y)=(\alpha _y(x),\beta (y))$
. Note that
![]() $\beta $
is unique given
$\beta $
is unique given
![]() $\sigma $
, and we denote it by
$\sigma $
, and we denote it by
![]() $\pi (\sigma )$
. Then the map
$\pi (\sigma )$
. Then the map
![]() $\sigma \mapsto \pi (\sigma )$
defines a surjective homomorphism from
$\sigma \mapsto \pi (\sigma )$
defines a surjective homomorphism from
![]() $G\wr H$
to H, and the kernel of this homomorphism is exactly
$G\wr H$
to H, and the kernel of this homomorphism is exactly
![]() $G^Y$
. Moreover the map
$G^Y$
. Moreover the map
![]() $e\colon \beta \mapsto ((x,y)\mapsto (x,\beta (y))$
splits the homomorphism
$e\colon \beta \mapsto ((x,y)\mapsto (x,\beta (y))$
splits the homomorphism
![]() $\pi $
, that is
$\pi $
, that is
![]() $\pi \circ e$
is the identity map on H. This implies that
$\pi \circ e$
is the identity map on H. This implies that
![]() $G\wr H$
can be written as a semidirect product
$G\wr H$
can be written as a semidirect product
![]() $G^Y\rtimes H$
(or more precisely
$G^Y\rtimes H$
(or more precisely
![]() $G^Y\rtimes e(H)$
).
$G^Y\rtimes e(H)$
).
In this document we are only interested in the case when the group H above is the full symmetric group.
Lemma 2.4. Let
![]() $G\leq \operatorname {Sym}(X)$
be a permutation group, and let Y be a set. Then:
$G\leq \operatorname {Sym}(X)$
be a permutation group, and let Y be a set. Then:
-
(1) if G is closed then so is
 $G\wr \operatorname {Sym}(Y)$
, and
$G\wr \operatorname {Sym}(Y)$
, and -
(2) if G is oligomorphic then so is
 $G\wr \operatorname {Sym}(Y)$
.
$G\wr \operatorname {Sym}(Y)$
.
Proof (1) A permutation
![]() $\sigma $
of
$\sigma $
of
![]() $X\times Y$
is contained in
$X\times Y$
is contained in
![]() $\operatorname {Sym}(X)\wr \operatorname {Sym}(Y)$
if and only if it preserves the equivalence relation
$\operatorname {Sym}(X)\wr \operatorname {Sym}(Y)$
if and only if it preserves the equivalence relation
![]() $E:=\{((x_1,y_1),(x_2,y_2))\colon y_1=y_2\}$
. This implies immediately that the group
$E:=\{((x_1,y_1),(x_2,y_2))\colon y_1=y_2\}$
. This implies immediately that the group
![]() $\operatorname {Sym}(X)\wr \operatorname {Sym}(Y)$
is closed. Now let
$\operatorname {Sym}(X)\wr \operatorname {Sym}(Y)$
is closed. Now let
![]() $(\sigma _n)_n$
be a sequence in
$(\sigma _n)_n$
be a sequence in
![]() $G\wr \operatorname {Sym}(Y)$
converging to a permutation
$G\wr \operatorname {Sym}(Y)$
converging to a permutation
![]() $\sigma \in \operatorname {Sym}(X\times Y)$
. Then there exist
$\sigma \in \operatorname {Sym}(X\times Y)$
. Then there exist
![]() $\beta _n\in \operatorname {Sym}(Y),\alpha _{y,n}\in G$
such that for all
$\beta _n\in \operatorname {Sym}(Y),\alpha _{y,n}\in G$
such that for all
![]() $x\in X$
and
$x\in X$
and
![]() $y\in Y$
we have
$y\in Y$
we have
![]() $\sigma _n(x,y)=(\alpha _{y,n}(x),\beta _n(y))$
. Since
$\sigma _n(x,y)=(\alpha _{y,n}(x),\beta _n(y))$
. Since
![]() $\operatorname {Sym}(X)\wr \operatorname {Sym}(Y)$
is closed we know that
$\operatorname {Sym}(X)\wr \operatorname {Sym}(Y)$
is closed we know that
![]() $\sigma \in \operatorname {Sym}(X)\wr \operatorname {Sym}(Y)$
, and thus there exist
$\sigma \in \operatorname {Sym}(X)\wr \operatorname {Sym}(Y)$
, and thus there exist
![]() $\beta \in \operatorname {Sym}(Y)$
and
$\beta \in \operatorname {Sym}(Y)$
and
![]() $\alpha _y\in \operatorname {Sym}(X)$
such that for all
$\alpha _y\in \operatorname {Sym}(X)$
such that for all
![]() $x\in X$
and
$x\in X$
and
![]() $y\in Y$
we have
$y\in Y$
we have
![]() $\sigma (x,y)=(\alpha _y(x),\beta (y))$
. We claim that the sequence
$\sigma (x,y)=(\alpha _y(x),\beta (y))$
. We claim that the sequence
![]() $(\alpha _{n,y})_n$
converges to
$(\alpha _{n,y})_n$
converges to
![]() $\alpha _y$
for all
$\alpha _y$
for all
![]() $y\in Y$
. Indeed let F be an arbitrary finite subset of X. Then since
$y\in Y$
. Indeed let F be an arbitrary finite subset of X. Then since
![]() $(\sigma _n)_n\rightarrow \sigma $
it follows that we can choose an index
$(\sigma _n)_n\rightarrow \sigma $
it follows that we can choose an index
![]() $n\in \omega $
such that for all
$n\in \omega $
such that for all
![]() $i\geq n$
we have
$i\geq n$
we have
![]() $\sigma |_{F\times \{y\}}=(g_i)|_{F\times \{y\}}$
for all
$\sigma |_{F\times \{y\}}=(g_i)|_{F\times \{y\}}$
for all
![]() $y\in Y$
, and thus
$y\in Y$
, and thus
![]() $\alpha _{i,y}|_F=\alpha _y|_F$
. We have shown that
$\alpha _{i,y}|_F=\alpha _y|_F$
. We have shown that
![]() $(\alpha _{n,y})_n$
converges to
$(\alpha _{n,y})_n$
converges to
![]() $\alpha _y$
, and thus
$\alpha _y$
, and thus
![]() $\alpha _y\in G$
since G is closed. This shows that
$\alpha _y\in G$
since G is closed. This shows that
![]() $\sigma \in G\wr \operatorname {Sym}(Y)$
.
$\sigma \in G\wr \operatorname {Sym}(Y)$
.
(2) Let
![]() $n\in \omega $
, and let Z be any n-element subset of Y. Note that in this case every n-orbit of
$n\in \omega $
, and let Z be any n-element subset of Y. Note that in this case every n-orbit of
![]() $G\wr \operatorname {Sym}(Y)$
contains a tuple in
$G\wr \operatorname {Sym}(Y)$
contains a tuple in
![]() $X\times Z$
. Indeed, if
$X\times Z$
. Indeed, if
![]() $\vec {a}\in (X\times Y)^n$
then
$\vec {a}\in (X\times Y)^n$
then
![]() $\vec {a}\in (X\times Z')^n$
for some
$\vec {a}\in (X\times Z')^n$
for some
![]() $Z'\subset Y$
with
$Z'\subset Y$
with
![]() $|Z'|\leq n$
. Let
$|Z'|\leq n$
. Let
![]() $\beta \in \operatorname {Sym}(Y)$
such that
$\beta \in \operatorname {Sym}(Y)$
such that
![]() $\beta (Z')\subset Z$
. Then the map
$\beta (Z')\subset Z$
. Then the map
![]() $(x,y)\mapsto (x,\beta (y))$
, which is contained in
$(x,y)\mapsto (x,\beta (y))$
, which is contained in
![]() $\{\operatorname {id}(X)\}\wr \operatorname {Sym}(Y)$
, maps
$\{\operatorname {id}(X)\}\wr \operatorname {Sym}(Y)$
, maps
![]() $\vec {a}$
into
$\vec {a}$
into
![]() $(X\times Z)^n$
. Let us also observe that
$(X\times Z)^n$
. Let us also observe that
![]() $(G\wr \operatorname {Sym}(Y))_{(Z)}=G\wr \operatorname {Sym}(Z)$
. In particular two n-tuples from
$(G\wr \operatorname {Sym}(Y))_{(Z)}=G\wr \operatorname {Sym}(Z)$
. In particular two n-tuples from
![]() $X\times Z$
are contained in the same orbit of
$X\times Z$
are contained in the same orbit of
![]() $G\wr \operatorname {Sym}(Z)$
if and only if they are contained in the same orbit of
$G\wr \operatorname {Sym}(Z)$
if and only if they are contained in the same orbit of
![]() $G\wr \operatorname {Sym}(Y)$
. From this it follows that
$G\wr \operatorname {Sym}(Y)$
. From this it follows that
![]() $o_n(G\wr \operatorname {Sym}(Y))=o_n(G\wr \operatorname {Sym}(Z))$
. We have already seen that the group
$o_n(G\wr \operatorname {Sym}(Y))=o_n(G\wr \operatorname {Sym}(Z))$
. We have already seen that the group
![]() $G^{Z}$
is oligomorphic. On the other hand
$G^{Z}$
is oligomorphic. On the other hand
![]() $G\wr \operatorname {Sym}(Z)$
contains
$G\wr \operatorname {Sym}(Z)$
contains
![]() $G^Z$
, and thus by Observation 2.3 it follows that
$G^Z$
, and thus by Observation 2.3 it follows that
![]() $G\wr \operatorname {Sym}(Z)$
is oligomorphic. In particular
$G\wr \operatorname {Sym}(Z)$
is oligomorphic. In particular
![]() $o_n(G\wr \operatorname {Sym}(Z))=o_n(G\wr \operatorname {Sym}(Z))$
is finite. Since this holds for all
$o_n(G\wr \operatorname {Sym}(Z))=o_n(G\wr \operatorname {Sym}(Z))$
is finite. Since this holds for all
![]() $n\in \omega $
it follows that
$n\in \omega $
it follows that
![]() $G\wr \operatorname {Sym}(Y)$
is oligomorphic.
$G\wr \operatorname {Sym}(Y)$
is oligomorphic.
2.6. Reducts of
 $\omega $
-categorical structures
$\omega $
-categorical structures
In this article every structure is assumed to be countable.
Notation 2.5. For a structure
![]() $\mathfrak {A}$
we denote by
$\mathfrak {A}$
we denote by
![]() $\Sigma (\mathfrak {A})$
the signature of
$\Sigma (\mathfrak {A})$
the signature of
![]() $\mathfrak {A}$
.
$\mathfrak {A}$
.
We say that a structure is relational if its signature does not contain any function symbols.
Notation 2.6. Let
![]() $\mathfrak {A}$
be a relational structure. Then for a relation R on
$\mathfrak {A}$
be a relational structure. Then for a relation R on
![]() $\mathfrak {A}$
we write
$\mathfrak {A}$
we write
![]() $\operatorname {ar}(R)$
for the arity of R. We denote by
$\operatorname {ar}(R)$
for the arity of R. We denote by
![]() $m(\mathfrak {A})$
the maximal arity of relations of
$m(\mathfrak {A})$
the maximal arity of relations of
![]() $\mathfrak {A}$
.
$\mathfrak {A}$
.
![]() $m(\mathfrak {A})$
is defined to be
$m(\mathfrak {A})$
is defined to be
![]() $\infty $
if such a maximum does not exist.
$\infty $
if such a maximum does not exist.
Remark 2.7. In this article we always assume that the signature of any structure contains the symbol “
![]() $=$
” (represented as equality). This means that the value of
$=$
” (represented as equality). This means that the value of
![]() $m(\mathfrak {A})$
is always at least 2.
$m(\mathfrak {A})$
is always at least 2.
Definition 2.8. Let
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
be structures. We say that
$\mathfrak {B}$
be structures. We say that
![]() $\mathfrak {B}$
is a reduct of
$\mathfrak {B}$
is a reduct of
![]() $\mathfrak {A}$
iff
$\mathfrak {A}$
iff
![]() $\operatorname {Dom}(\mathfrak {A})=\operatorname {Dom}(\mathfrak {B})$
and every relation, function, and constant of
$\operatorname {Dom}(\mathfrak {A})=\operatorname {Dom}(\mathfrak {B})$
and every relation, function, and constant of
![]() $\mathfrak {B}$
is first-order definable in
$\mathfrak {B}$
is first-order definable in
![]() $\mathfrak {A}$
. Two structures are called interdefinable if they are reducts of one another.
$\mathfrak {A}$
. Two structures are called interdefinable if they are reducts of one another.
The structures
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
are called bidefinable iff there exist a reduct
$\mathfrak {B}$
are called bidefinable iff there exist a reduct
![]() $\mathfrak {A}'$
of
$\mathfrak {A}'$
of
![]() $\mathfrak {A}$
with
$\mathfrak {A}$
with
![]() $\Sigma (\mathfrak {A}')=\Sigma (\mathfrak {B})$
, a reduct
$\Sigma (\mathfrak {A}')=\Sigma (\mathfrak {B})$
, a reduct
![]() $\mathfrak {B}'$
of
$\mathfrak {B}'$
of
![]() $\mathfrak {B}$
with
$\mathfrak {B}$
with
![]() $\Sigma (\mathfrak {B}')=\Sigma (\mathfrak {A})$
, and a bijection i from A to B such that i defines an isomorphism from
$\Sigma (\mathfrak {B}')=\Sigma (\mathfrak {A})$
, and a bijection i from A to B such that i defines an isomorphism from
![]() $\mathfrak {A}$
to
$\mathfrak {A}$
to
![]() $\mathfrak {B}'$
and from
$\mathfrak {B}'$
and from
![]() $\mathfrak {A}'$
to
$\mathfrak {A}'$
to
![]() $\mathfrak {B}$
.
$\mathfrak {B}$
.
We say that
![]() $\mathfrak {B}$
is a finite-index reduct of
$\mathfrak {B}$
is a finite-index reduct of
![]() $\mathfrak {A}$
iff
$\mathfrak {A}$
iff
![]() $|\operatorname {Aut}(\mathfrak {B}):\operatorname {Aut}(\mathfrak {A})|$
is finite.
$|\operatorname {Aut}(\mathfrak {B}):\operatorname {Aut}(\mathfrak {A})|$
is finite.
Lemma 2.9. The structures
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
are bidefinable if and only if
$\mathfrak {B}$
are bidefinable if and only if
![]() $\mathfrak {B}$
is interdefinable with a structure which is isomorphic to
$\mathfrak {B}$
is interdefinable with a structure which is isomorphic to
![]() $\mathfrak {A}$
.
$\mathfrak {A}$
.
Proof Let us assume that
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
are bidefinable, and let
$\mathfrak {B}$
are bidefinable, and let
![]() $\mathfrak {B}'$
and
$\mathfrak {B}'$
and
![]() $\mathfrak {A}'$
be structures and let
$\mathfrak {A}'$
be structures and let
![]() $i\colon A\rightarrow B$
be a bijection witnessing this. Then by definition
$i\colon A\rightarrow B$
be a bijection witnessing this. Then by definition
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}'$
are isomorphic, and we claim that
$\mathfrak {B}'$
are isomorphic, and we claim that
![]() $\mathfrak {B}$
and
$\mathfrak {B}$
and
![]() $\mathfrak {B}'$
are interdefinable. To see this, it suffices to show that
$\mathfrak {B}'$
are interdefinable. To see this, it suffices to show that
![]() $\mathfrak {B}$
is a reduct of
$\mathfrak {B}$
is a reduct of
![]() $\mathfrak {B}'$
. But this follows from the fact that
$\mathfrak {B}'$
. But this follows from the fact that
![]() $\mathfrak {A}'$
is a reduct of
$\mathfrak {A}'$
is a reduct of
![]() $\mathfrak {A}$
, and i defines an isomorphism from
$\mathfrak {A}$
, and i defines an isomorphism from
![]() $\mathfrak {A}'$
to
$\mathfrak {A}'$
to
![]() $\mathfrak {B}$
and from
$\mathfrak {B}$
and from
![]() $\mathfrak {A}$
to
$\mathfrak {A}$
to
![]() $\mathfrak {B}'$
. This finishes the proof of the “only if” direction of the lemma.
$\mathfrak {B}'$
. This finishes the proof of the “only if” direction of the lemma.
Now let us assume that
![]() $\mathfrak {B}$
and
$\mathfrak {B}$
and
![]() $\mathfrak {B}'$
are interdefinable, and
$\mathfrak {B}'$
are interdefinable, and
![]() $\mathfrak {B}'$
and
$\mathfrak {B}'$
and
![]() $\mathfrak {A}$
are isomorphic. Let i be an isomorphism from
$\mathfrak {A}$
are isomorphic. Let i be an isomorphism from
![]() $\mathfrak {A}$
to
$\mathfrak {A}$
to
![]() $\mathfrak {B}'$
. Let us define the structure
$\mathfrak {B}'$
. Let us define the structure
![]() $\mathfrak {A}'$
as follows. The domain set of
$\mathfrak {A}'$
as follows. The domain set of
![]() $\mathfrak {A}'$
is A,
$\mathfrak {A}'$
is A,
![]() $\Sigma (\mathfrak {A}')=\Sigma (\mathfrak {B})$
, and every symbol in
$\Sigma (\mathfrak {A}')=\Sigma (\mathfrak {B})$
, and every symbol in
![]() $\Sigma (\mathfrak {B})$
is realized in
$\Sigma (\mathfrak {B})$
is realized in
![]() $\mathfrak {A}'$
in such a way that i defines an isomorphism from
$\mathfrak {A}'$
in such a way that i defines an isomorphism from
![]() $\mathfrak {A}'$
to
$\mathfrak {A}'$
to
![]() $\mathfrak {B}$
. By definition
$\mathfrak {B}$
. By definition
![]() $\mathfrak {B}'$
is a reduct of
$\mathfrak {B}'$
is a reduct of
![]() $\mathfrak {B}$
. It remains to show that
$\mathfrak {B}$
. It remains to show that
![]() $\mathfrak {A}'$
is also a reduct of
$\mathfrak {A}'$
is also a reduct of
![]() $\mathfrak {A}$
. By definition
$\mathfrak {A}$
. By definition
![]() $\mathfrak {B}$
is also a reduct of
$\mathfrak {B}$
is also a reduct of
![]() $\mathfrak {B}'$
. Since
$\mathfrak {B}'$
. Since
![]() $i^{-1}$
defines an isomorphism from
$i^{-1}$
defines an isomorphism from
![]() $\mathfrak {B}'$
to
$\mathfrak {B}'$
to
![]() $\mathfrak {A}$
and from
$\mathfrak {A}$
and from
![]() $\mathfrak {B}$
to
$\mathfrak {B}$
to
![]() $\mathfrak {A}'$
, we obtain that
$\mathfrak {A}'$
, we obtain that
![]() $i^{-1}(\mathfrak {B})=\mathfrak {A}'$
is a reduct of
$i^{-1}(\mathfrak {B})=\mathfrak {A}'$
is a reduct of
![]() $i^{-1}(\mathfrak {B}')=\mathfrak {A}$
. Thus
$i^{-1}(\mathfrak {B}')=\mathfrak {A}$
. Thus
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
are bidefinable.
$\mathfrak {B}$
are bidefinable.
From now on we use the description given in Lemma 2.9 for bidefinability instead of its definition. The reason why we did not define bidefinability this way is that from this description it is not obvious that bidefinability is a symmetric relation.
Remark 2.10. Clearly interdefinability implies bidefinability, but the converse implication does not hold necessarily even if the structures are assumed to have the same domain set. For instance the structures
![]() $(\mathbb {N};=,0)$
and
$(\mathbb {N};=,0)$
and
![]() $(\mathbb {N};=,1)$
are bidefinable but not interdefinable.
$(\mathbb {N};=,1)$
are bidefinable but not interdefinable.
When we are talking about reducts of a given structure
![]() $\mathfrak {A}$
we usually consider two reducts the same if they are interdefinable. It turns out that under the assumption that
$\mathfrak {A}$
we usually consider two reducts the same if they are interdefinable. It turns out that under the assumption that
![]() $\mathfrak {A}$
is
$\mathfrak {A}$
is
![]() $\omega $
-categorical the reducts of
$\omega $
-categorical the reducts of
![]() $\mathfrak {A}$
are completely described by the closed supergroups of the automorphism of
$\mathfrak {A}$
are completely described by the closed supergroups of the automorphism of
![]() $\mathfrak {A}$
(see Theorem 2.13).
$\mathfrak {A}$
(see Theorem 2.13).
Definition 2.11. A countable structure
![]() $\mathfrak {A}$
is called
$\mathfrak {A}$
is called
![]() $\omega $
-categorical if and only if it is isomorphic to every countable model of its first-order theory.
$\omega $
-categorical if and only if it is isomorphic to every countable model of its first-order theory.
By the theorem of Engeler, Ryll-Nardzewski, and Svenonius, we know that a countably structure
![]() $\mathfrak {A}$
is
$\mathfrak {A}$
is
![]() $\omega $
-categorical if and only if
$\omega $
-categorical if and only if
![]() $\operatorname {Aut}(\mathfrak {A})$
is oligomorphic (see for instance [Reference Hodges29]). Given a structure
$\operatorname {Aut}(\mathfrak {A})$
is oligomorphic (see for instance [Reference Hodges29]). Given a structure
![]() $\mathfrak {A}$
we use the notation
$\mathfrak {A}$
we use the notation
![]() $f_n(\mathfrak {A})$
for
$f_n(\mathfrak {A})$
for
![]() $f_n(\operatorname {Aut}(\mathfrak {A}))$
where n is a positive integer and f is any of the operators
$f_n(\operatorname {Aut}(\mathfrak {A}))$
where n is a positive integer and f is any of the operators
![]() $o,o^i$
, or
$o,o^i$
, or
![]() $o^s$
(see Definition 2.1). Then Observation 2.3 has the following analog for structures and reducts.
$o^s$
(see Definition 2.1). Then Observation 2.3 has the following analog for structures and reducts.
Lemma 2.12. Let
![]() $\mathfrak {B}$
be a reduct of a structure
$\mathfrak {B}$
be a reduct of a structure
![]() $\mathfrak {A}$
. Then
$\mathfrak {A}$
. Then
![]() $f_n(\mathfrak {B})\leq f_n(\mathfrak {A})$
where f is any of the operators
$f_n(\mathfrak {B})\leq f_n(\mathfrak {A})$
where f is any of the operators
![]() $o,o^i$
, or
$o,o^i$
, or
![]() $o^s$
. In particular every reduct of an
$o^s$
. In particular every reduct of an
![]() $\omega $
-categorical structure is
$\omega $
-categorical structure is
![]() $\omega $
-categorical.
$\omega $
-categorical.
We also know that for an
![]() $\omega $
-categorical structure
$\omega $
-categorical structure
![]() $\mathfrak {A}$
a relation (or a function or a constant) defined on A is first-order definable if and only if it is preserved by every automorphism of
$\mathfrak {A}$
a relation (or a function or a constant) defined on A is first-order definable if and only if it is preserved by every automorphism of
![]() $\mathfrak {A}$
(see [Reference Hodges29]). This implies the following theorem.
$\mathfrak {A}$
(see [Reference Hodges29]). This implies the following theorem.
Theorem 2.13. Let
![]() $\mathfrak {A}$
be a countable
$\mathfrak {A}$
be a countable
![]() $\omega $
-categorical structure. Then every closed group
$\omega $
-categorical structure. Then every closed group
![]() $\operatorname {Aut}(\mathfrak {A})\subset G\subset \operatorname {Sym}(A)$
is an automorphism group of a reduct of
$\operatorname {Aut}(\mathfrak {A})\subset G\subset \operatorname {Sym}(A)$
is an automorphism group of a reduct of
![]() $\mathfrak {A}$
, and two reducts of
$\mathfrak {A}$
, and two reducts of
![]() $\mathfrak {A}$
have the same automorphism group if and only if they are interdefinable.
$\mathfrak {A}$
have the same automorphism group if and only if they are interdefinable.
Theorem 2.13 tells us that given a countable
![]() $\omega $
-categorical structure
$\omega $
-categorical structure
![]() $\mathfrak {A}$
the map
$\mathfrak {A}$
the map
![]() $\mathfrak {B}\mapsto \operatorname {Aut}(\mathfrak {B})$
defines a bijection between the reducts of
$\mathfrak {B}\mapsto \operatorname {Aut}(\mathfrak {B})$
defines a bijection between the reducts of
![]() $\mathfrak {A}$
(up to interdefinability), and the closed supergroups of
$\mathfrak {A}$
(up to interdefinability), and the closed supergroups of
![]() $\operatorname {Aut}(\mathfrak {A})$
, that is the closed permutation groups containing
$\operatorname {Aut}(\mathfrak {A})$
, that is the closed permutation groups containing
![]() $\operatorname {Aut}(\mathfrak {A})$
.
$\operatorname {Aut}(\mathfrak {A})$
.
An easy consequence of Theorem 2.13 is the following.
Lemma 2.14. Let
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
be countable structures, so that at least one of them is
$\mathfrak {B}$
be countable structures, so that at least one of them is
![]() $\omega $
-categorical. Then
$\omega $
-categorical. Then
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
are bidefinable if and only if
$\mathfrak {B}$
are bidefinable if and only if
![]() $\operatorname {Aut}(\mathfrak {A})$
and
$\operatorname {Aut}(\mathfrak {A})$
and
![]() $\operatorname {Aut}(\mathfrak {B})$
are isomorphic as permutation groups.
$\operatorname {Aut}(\mathfrak {B})$
are isomorphic as permutation groups.
Proof We can assume without loss of generality that
![]() $\mathfrak {A}$
is
$\mathfrak {A}$
is
![]() $\omega $
-categorical.
$\omega $
-categorical.
Suppose first that
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
are bidefinable. Then by Lemma 2.9 we know that
$\mathfrak {B}$
are bidefinable. Then by Lemma 2.9 we know that
![]() $\mathfrak {B}$
is interdefinable with some structure
$\mathfrak {B}$
is interdefinable with some structure
![]() $\mathfrak {B}'$
which is isomorphic to
$\mathfrak {B}'$
which is isomorphic to
![]() $\mathfrak {A}$
. Then
$\mathfrak {A}$
. Then
![]() $\operatorname {Aut}(\mathfrak {B})=\operatorname {Aut}(\mathfrak {B}')$
and it is isomorphic to
$\operatorname {Aut}(\mathfrak {B})=\operatorname {Aut}(\mathfrak {B}')$
and it is isomorphic to
![]() $\operatorname {Aut}(\mathfrak {A})$
.
$\operatorname {Aut}(\mathfrak {A})$
.
For the other direction let i be a bijection from A to B such that i induces an isomorphism from
![]() $\operatorname {Aut}(\mathfrak {A})$
to
$\operatorname {Aut}(\mathfrak {A})$
to
![]() $\operatorname {Aut}(\mathfrak {B})$
. Let
$\operatorname {Aut}(\mathfrak {B})$
. Let
![]() $\mathfrak {A}':=i^{-1}(\mathfrak {B})$
. Then we have
$\mathfrak {A}':=i^{-1}(\mathfrak {B})$
. Then we have
![]() $\operatorname {Aut}(\mathfrak {A}')=\iota (i^{-1})\operatorname {Aut}(\mathfrak {B})=\iota (i^{-1})(\iota (i)(\operatorname {Aut}(\mathfrak {A})))=\operatorname {Aut}(\mathfrak {A})$
. Theorem 2.13 then implies that
$\operatorname {Aut}(\mathfrak {A}')=\iota (i^{-1})\operatorname {Aut}(\mathfrak {B})=\iota (i^{-1})(\iota (i)(\operatorname {Aut}(\mathfrak {A})))=\operatorname {Aut}(\mathfrak {A})$
. Theorem 2.13 then implies that
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {A}'$
are interdefinable. On the other hand it follows from the definition that
$\mathfrak {A}'$
are interdefinable. On the other hand it follows from the definition that
![]() $\mathfrak {A}'$
is isomorphic to
$\mathfrak {A}'$
is isomorphic to
![]() $\mathfrak {B}$
. Therefore by Lemma 2.9 the structures
$\mathfrak {B}$
. Therefore by Lemma 2.9 the structures
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
are bidefinable.
$\mathfrak {B}$
are bidefinable.
Lemma 2.14, combined with Theorem 2.13 implies that for a countable
![]() $\omega $
-categorical structure the map
$\omega $
-categorical structure the map
![]() $\mathfrak {B}\mapsto \operatorname {Aut}(\mathfrak {B})$
defines a bijection between the reducts of
$\mathfrak {B}\mapsto \operatorname {Aut}(\mathfrak {B})$
defines a bijection between the reducts of
![]() $\mathfrak {A}$
up to bidefinability, and the closed supergroups of
$\mathfrak {A}$
up to bidefinability, and the closed supergroups of
![]() $\operatorname {Aut}(\mathfrak {A})$
up to isomorphism.
$\operatorname {Aut}(\mathfrak {A})$
up to isomorphism.
2.7. Homogeneous structures, Thomas’ conjecture
Definition 2.15. A structure
![]() $\mathfrak {A}$
is called homogeneous if every isomorphism between finitely generated substructures of
$\mathfrak {A}$
is called homogeneous if every isomorphism between finitely generated substructures of
![]() $\mathfrak {A}$
can be extended to an automorphism of
$\mathfrak {A}$
can be extended to an automorphism of
![]() $\mathfrak {A}$
.
$\mathfrak {A}$
.
Fact 2.16. Every homogeneous structure with a finite relational signature is
![]() $\omega $
-categorical.
$\omega $
-categorical.
Proof Let
![]() $\mathfrak {A}$
be a homogeneous structure with a finite relational signature
$\mathfrak {A}$
be a homogeneous structure with a finite relational signature
![]() $\tau $
. We show that
$\tau $
. We show that
![]() $\operatorname {Aut}(\mathfrak {A})$
is oligomorphic. Since
$\operatorname {Aut}(\mathfrak {A})$
is oligomorphic. Since
![]() $\tau $
is finite, and only contains relational and constant symbols, it follows that every finitely generated substructure is finite. Then using the finiteness of
$\tau $
is finite, and only contains relational and constant symbols, it follows that every finitely generated substructure is finite. Then using the finiteness of
![]() $\tau $
again it follows that for all
$\tau $
again it follows that for all
![]() $n\in \omega $
there exist only finitely many
$n\in \omega $
there exist only finitely many
![]() $\tau $
-structures up to isomorphism. In particular
$\tau $
-structures up to isomorphism. In particular
![]() $\mathfrak {A}$
has finitely many quantifier-free types. It follows from the homogeneity of
$\mathfrak {A}$
has finitely many quantifier-free types. It follows from the homogeneity of
![]() $\mathfrak {A}$
that if two n-tuples have the same quantifier-free type then they are in the same orbit of
$\mathfrak {A}$
that if two n-tuples have the same quantifier-free type then they are in the same orbit of
![]() $\operatorname {Aut}(\mathfrak {A})$
. This implies that
$\operatorname {Aut}(\mathfrak {A})$
. This implies that
![]() $o_n(\mathfrak {A})$
is finite. Therefore
$o_n(\mathfrak {A})$
is finite. Therefore
![]() $\operatorname {Aut}(\mathfrak {A})$
is oligomorphic.
$\operatorname {Aut}(\mathfrak {A})$
is oligomorphic.
Thomas [Reference Thomas37] conjectured that every homogeneous structure
![]() $\mathfrak {A}$
with a finite relational signature has only finitely many reducts up to interdefinability.
$\mathfrak {A}$
with a finite relational signature has only finitely many reducts up to interdefinability.
The fact that a given
![]() $\omega $
-categorical structure has finitely many reducts can be formulated in many different ways, as the following proposition shows.
$\omega $
-categorical structure has finitely many reducts can be formulated in many different ways, as the following proposition shows.
Proposition 2.17. Let
![]() $\mathfrak {A}$
be a countable
$\mathfrak {A}$
be a countable
![]() $\omega $
-categorical structure. Then the following are equivalent:
$\omega $
-categorical structure. Then the following are equivalent:
-
(1)
 $\mathfrak {A}$
has finitely many reducts up to interdefinability.
$\mathfrak {A}$
has finitely many reducts up to interdefinability. -
(2)
 $\mathfrak {A}$
has finitely many reducts up to bidefinability.
$\mathfrak {A}$
has finitely many reducts up to bidefinability. -
(3) There exists some
 $N\in \omega $
such that every reduct of
$N\in \omega $
such that every reduct of
 $\mathfrak {A}$
is interdefinable with a relational structure
$\mathfrak {A}$
is interdefinable with a relational structure
 $\mathfrak {B}$
with
$\mathfrak {B}$
with
 $m(\mathfrak {B})\leq N$
.
$m(\mathfrak {B})\leq N$
. -
(4)
 $\operatorname {Aut}(\mathfrak {A})$
has finitely many closed supergroups in
$\operatorname {Aut}(\mathfrak {A})$
has finitely many closed supergroups in
 $\operatorname {Sym}(A)$
.
$\operatorname {Sym}(A)$
. -
(5)
 $\operatorname {Aut}(\mathfrak {A})$
has finitely many closed non-isomorphic supergroups in
$\operatorname {Aut}(\mathfrak {A})$
has finitely many closed non-isomorphic supergroups in
 $\operatorname {Sym}(A)$
.
$\operatorname {Sym}(A)$
.
Proof The equivalence of items (1) and (2) is Proposition 6.36 in [Reference Bodirsky and Bodor11]. For the direction (1)
![]() $\rightarrow $
(3) we only need to show that item (1) implies that every reduct of
$\rightarrow $
(3) we only need to show that item (1) implies that every reduct of
![]() $\mathfrak {A}$
is interdefinable with a structure with a finite relational signature. This follows for instance from Lemma 6.35 in [Reference Bodirsky and Bodor11].
$\mathfrak {A}$
is interdefinable with a structure with a finite relational signature. This follows for instance from Lemma 6.35 in [Reference Bodirsky and Bodor11].
In order to show the implication (3)
![]() $\rightarrow $
(1) it is enough to show that
$\rightarrow $
(1) it is enough to show that
![]() $\mathfrak {A}$
has finitely many reducts
$\mathfrak {A}$
has finitely many reducts
![]() $\mathfrak {B}$
with
$\mathfrak {B}$
with
![]() $m(\mathfrak {B})\leq N$
up to interdefinability. Let R be a relation of
$m(\mathfrak {B})\leq N$
up to interdefinability. Let R be a relation of
![]() $\mathfrak {B}$
with arity at most N. Then R is interdefinable with the relation
$\mathfrak {B}$
with arity at most N. Then R is interdefinable with the relation
![]() $\{(x_1,\dots ,x_N)\colon (x_1,\dots ,x_{\operatorname {ar}(R)})\in R\}$
. Therefore we can assume without loss of generality that every relation of
$\{(x_1,\dots ,x_N)\colon (x_1,\dots ,x_{\operatorname {ar}(R)})\in R\}$
. Therefore we can assume without loss of generality that every relation of
![]() $\mathfrak {B}$
is N-ary. Since
$\mathfrak {B}$
is N-ary. Since
![]() $\mathfrak {B}$
is a reduct of
$\mathfrak {B}$
is a reduct of
![]() $\mathfrak {A}$
it follows that every N-ary relation of
$\mathfrak {A}$
it follows that every N-ary relation of
![]() $\mathfrak {B}$
is a union of some orbits of
$\mathfrak {B}$
is a union of some orbits of
![]() $\mathfrak {A}$
. Therefore there are at most
$\mathfrak {A}$
. Therefore there are at most
![]() $2^{o_N(\mathfrak {A})}$
many possible choices for an N-ary relation of
$2^{o_N(\mathfrak {A})}$
many possible choices for an N-ary relation of
![]() $\mathfrak {B}$
, and hence there are at most
$\mathfrak {B}$
, and hence there are at most
![]() $2^{2^{o_N(\mathfrak {A})}}$
many choices for reducts
$2^{2^{o_N(\mathfrak {A})}}$
many choices for reducts
![]() $\mathfrak {B}$
of
$\mathfrak {B}$
of
![]() $\mathfrak {A}$
with
$\mathfrak {A}$
with
![]() $m(\mathfrak {B})\leq N$
. Since
$m(\mathfrak {B})\leq N$
. Since
![]() $\mathfrak {A}$
is
$\mathfrak {A}$
is
![]() $\omega $
-categorical we know that
$\omega $
-categorical we know that
![]() $o_N(\mathfrak {A})$
is finite, and hence
$o_N(\mathfrak {A})$
is finite, and hence
![]() $2^{2^{o_N(\mathfrak {A})}}$
is also finite.
$2^{2^{o_N(\mathfrak {A})}}$
is also finite.
The equivalences (1)
![]() $\leftrightarrow $
(4) and (2)
$\leftrightarrow $
(4) and (2)
![]() $\leftrightarrow $
(5) follow from Theorem 2.13 and Lemma 2.14.
$\leftrightarrow $
(5) follow from Theorem 2.13 and Lemma 2.14.
Definition 2.18. We call a structure finitely homogenizable if it is interdefinable with a homogeneous structure with a finite relational signature.
We denote by
![]() $\mathcal {FH}$
the class of finitely homogenizable structures.
$\mathcal {FH}$
the class of finitely homogenizable structures.
Clearly the class
![]() $\mathcal {FH}$
is closed under bidefinability, and by Fact 2.16 we know that every structure in
$\mathcal {FH}$
is closed under bidefinability, and by Fact 2.16 we know that every structure in
![]() $\mathcal {FH}$
is
$\mathcal {FH}$
is
![]() $\omega $
-categorical. Thus it follows from Lemma 2.14 that the structures in
$\omega $
-categorical. Thus it follows from Lemma 2.14 that the structures in
![]() $\mathcal {FH}$
can fully be described in terms of their automorphisms groups. We give a concrete such description below, as well as other equivalent conditions to check whether a structure is contained in the class
$\mathcal {FH}$
can fully be described in terms of their automorphisms groups. We give a concrete such description below, as well as other equivalent conditions to check whether a structure is contained in the class
![]() $\mathcal {FH}$
. We first need a couple of notations.
$\mathcal {FH}$
. We first need a couple of notations.
Notation 2.19. For a tuple
![]() $\vec {a}\in X^n$
we denote by
$\vec {a}\in X^n$
we denote by
![]() $a_i$
the ith coordinate of
$a_i$
the ith coordinate of
![]() $\vec {a}$
. For a function
$\vec {a}$
. For a function
![]() $\pi \colon k\rightarrow n$
we denote by
$\pi \colon k\rightarrow n$
we denote by
![]() $\vec {a}_{\pi }$
the tuple
$\vec {a}_{\pi }$
the tuple
![]() $(a_{\pi (0)},\dots ,a_{\pi (k-1)})$
.
$(a_{\pi (0)},\dots ,a_{\pi (k-1)})$
.
Notation 2.20. Let
![]() $\mathfrak {A}$
be a relational structure, and let
$\mathfrak {A}$
be a relational structure, and let
![]() $m\in \omega $
. Then we denote by
$m\in \omega $
. Then we denote by
![]() $\Delta _m(\mathfrak {A})$
the structure whose domain is A, and whose relations are all subsets of
$\Delta _m(\mathfrak {A})$
the structure whose domain is A, and whose relations are all subsets of
![]() $A^m$
which are definable in
$A^m$
which are definable in
![]() $\mathfrak {A}$
.
$\mathfrak {A}$
.
It is clear from the definition that if
![]() $m'\leq m$
then every
$m'\leq m$
then every
![]() $m'$
-ary relation of
$m'$
-ary relation of
![]() $\mathfrak {A}$
is quantifier-free definable in
$\mathfrak {A}$
is quantifier-free definable in
![]() $\Delta _m(\mathfrak {A})$
, that is
$\Delta _m(\mathfrak {A})$
, that is
![]() $\Delta _{m'}(\mathfrak {A})$
is a quantifier-free reduct of
$\Delta _{m'}(\mathfrak {A})$
is a quantifier-free reduct of
![]() $\Delta _m(\mathfrak {A})$
.
$\Delta _m(\mathfrak {A})$
.
If
![]() $\mathfrak {A}$
is
$\mathfrak {A}$
is
![]() $\omega $
-categorical then every type over
$\omega $
-categorical then every type over
![]() $\mathfrak {A}$
is principal, and thus in this case
$\mathfrak {A}$
is principal, and thus in this case
![]() $\Delta _m(\mathfrak {A})$
is a first-order reduct of
$\Delta _m(\mathfrak {A})$
is a first-order reduct of
![]() $\mathfrak {A}$
for all
$\mathfrak {A}$
for all
![]() $m\in \omega $
.
$m\in \omega $
.
For a structure
![]() $\mathfrak {A}$
and tuples
$\mathfrak {A}$
and tuples
![]() $\vec {u},\vec {v}\in A^n$
we write
$\vec {u},\vec {v}\in A^n$
we write
![]() $\vec {u}\approx _{\mathfrak {A}}\vec {v}$
iff
$\vec {u}\approx _{\mathfrak {A}}\vec {v}$
iff
![]() $\vec {u}$
and
$\vec {u}$
and
![]() $\vec {v}$
have the same type over
$\vec {v}$
have the same type over
![]() $\mathfrak {A}$
, and we write
$\mathfrak {A}$
, and we write
![]() $\vec {u}\not \approx _{\mathfrak {A}} \vec {v}$
iff
$\vec {u}\not \approx _{\mathfrak {A}} \vec {v}$
iff
![]() $\vec {u}\approx _{\mathfrak {A}} \vec {v}$
does not hold. In the case when
$\vec {u}\approx _{\mathfrak {A}} \vec {v}$
does not hold. In the case when
![]() $\mathfrak {A}$
is
$\mathfrak {A}$
is
![]() $\omega $
-categorical
$\omega $
-categorical
![]() $\vec {u}\approx _{\mathfrak {A}} \vec {v}$
holds if and only if
$\vec {u}\approx _{\mathfrak {A}} \vec {v}$
holds if and only if
![]() $\vec {u}$
and
$\vec {u}$
and
![]() $\vec {v}$
are in the same orbit of
$\vec {v}$
are in the same orbit of
![]() $\operatorname {Aut}(\mathfrak {A})$
.
$\operatorname {Aut}(\mathfrak {A})$
.
Lemma 2.21. Let
![]() $\mathfrak {A}$
be an
$\mathfrak {A}$
be an
![]() $\omega $
-categorical structure, and let
$\omega $
-categorical structure, and let
![]() $m\geq 2$
. Then the following are equivalent:
$m\geq 2$
. Then the following are equivalent:
-
(1)
 $\mathfrak {A}$
is interdefinable with a homogeneous relational signature structure
$\mathfrak {A}$
is interdefinable with a homogeneous relational signature structure
 $\mathfrak {A}'$
with
$\mathfrak {A}'$
with
 $m(\mathfrak {A}')\leq m$
.
$m(\mathfrak {A}')\leq m$
. -
(2)
 $\mathfrak {A}$
is interdefinable with a homogeneous relational signature structure all of whose relations have arity exactly m.
$\mathfrak {A}$
is interdefinable with a homogeneous relational signature structure all of whose relations have arity exactly m. -
(3)
 $\mathfrak {A}$
and
$\mathfrak {A}$
and
 $\Delta _m(\mathfrak {A})$
are interdefinable, and
$\Delta _m(\mathfrak {A})$
are interdefinable, and
 $\Delta _m(\mathfrak {A})$
is homogeneous.
$\Delta _m(\mathfrak {A})$
is homogeneous. -
(4) For all
 $\vec {u},\vec {v}\in A^n$
if
$\vec {u},\vec {v}\in A^n$
if
 $\vec {u}\not \approx _{\mathfrak {A}}\vec {v}$
then there exists a function
$\vec {u}\not \approx _{\mathfrak {A}}\vec {v}$
then there exists a function
 $\pi \colon m\rightarrow n$
such that
$\pi \colon m\rightarrow n$
such that
 $\vec {u}_{\pi }\not \approx _{\mathfrak {A}}\vec {v}_{\pi }$
.
$\vec {u}_{\pi }\not \approx _{\mathfrak {A}}\vec {v}_{\pi }$
.
Proof The implication (2)
![]() $\rightarrow $
(1) is obvious. The converse follows from the fact that if
$\rightarrow $
(1) is obvious. The converse follows from the fact that if
![]() $m'\leq m$
then every
$m'\leq m$
then every
![]() $m'$
-ary relation of
$m'$
-ary relation of
![]() $\mathfrak {A}'$
is quantifier-free definable from an m-ary relation of
$\mathfrak {A}'$
is quantifier-free definable from an m-ary relation of
![]() $\mathfrak {A}'$
.
$\mathfrak {A}'$
.
The implication (3)
![]() $\rightarrow $
(2) is obvious. For the converse implication let us assume that item (2) holds, and let
$\rightarrow $
(2) is obvious. For the converse implication let us assume that item (2) holds, and let
![]() $\mathfrak {A}'$
be a structure as it is dictated in the condition. Then
$\mathfrak {A}'$
be a structure as it is dictated in the condition. Then
![]() $\Delta _m(\mathfrak {A})=\Delta _m(\mathfrak {A}')$
. Since
$\Delta _m(\mathfrak {A})=\Delta _m(\mathfrak {A}')$
. Since
![]() $\mathfrak {A}$
, and thus also
$\mathfrak {A}$
, and thus also
![]() $\mathfrak {A}'$
is
$\mathfrak {A}'$
is
![]() $\omega $
-categorical it follows that every definable relation of
$\omega $
-categorical it follows that every definable relation of
![]() $\mathfrak {A}'$
of arity m is a finite union of some m-orbits of
$\mathfrak {A}'$
of arity m is a finite union of some m-orbits of
![]() $\mathfrak {A}'$
. Therefore
$\mathfrak {A}'$
. Therefore
![]() $\mathfrak {A}'$
is quantifier-free definable in
$\mathfrak {A}'$
is quantifier-free definable in
![]() $\Delta _m(\mathfrak {A}')$
. Since
$\Delta _m(\mathfrak {A}')$
. Since
![]() $\Delta _m(\mathfrak {A}')$
is reduct of
$\Delta _m(\mathfrak {A}')$
is reduct of
![]() $\mathfrak {A}'$
and
$\mathfrak {A}'$
and
![]() $\mathfrak {A}'$
is homogeneous it follows that
$\mathfrak {A}'$
is homogeneous it follows that
![]() $\Delta _m(\mathfrak {A}')$
is also quantifier-free definable in
$\Delta _m(\mathfrak {A}')$
is also quantifier-free definable in
![]() $\mathfrak {A}'$
. Therefore
$\mathfrak {A}'$
. Therefore
![]() $\Delta _m(\mathfrak {A}')$
is interdefinable with
$\Delta _m(\mathfrak {A}')$
is interdefinable with
![]() $\mathfrak {A}$
, and it is homogeneous.
$\mathfrak {A}$
, and it is homogeneous.
(3)
![]() $\rightarrow $
(4). Let us assume that condition (3) holds. We can assume without loss of generality that
$\rightarrow $
(4). Let us assume that condition (3) holds. We can assume without loss of generality that
![]() $\mathfrak {A}=\Delta _m(\mathfrak {A})$
. We show the contrapositive of the statement in item (4). Let us assume that for all
$\mathfrak {A}=\Delta _m(\mathfrak {A})$
. We show the contrapositive of the statement in item (4). Let us assume that for all
![]() $\pi \colon m\rightarrow n$
we have
$\pi \colon m\rightarrow n$
we have
![]() $\vec {u}_{\pi }\approx _{\mathfrak {A}}\vec {v}_{\pi }$
. Then by definition we have
$\vec {u}_{\pi }\approx _{\mathfrak {A}}\vec {v}_{\pi }$
. Then by definition we have
![]() $R(\vec {u}_{\pi })\Leftrightarrow R(\vec {v}_{\pi })$
for all
$R(\vec {u}_{\pi })\Leftrightarrow R(\vec {v}_{\pi })$
for all
![]() $\pi \colon m\rightarrow n$
and for all relations R of
$\pi \colon m\rightarrow n$
and for all relations R of
![]() $\mathfrak {A}$
with arity m. Since
$\mathfrak {A}$
with arity m. Since
![]() $\mathfrak {A}=\Delta _m(\mathfrak {A})$
we know that the arity of every relation of
$\mathfrak {A}=\Delta _m(\mathfrak {A})$
we know that the arity of every relation of
![]() $\mathfrak {A}$
is exactly m. This means that the tuples
$\mathfrak {A}$
is exactly m. This means that the tuples
![]() $\vec {u}$
and
$\vec {u}$
and
![]() $\vec {v}$
have the same atomic type over
$\vec {v}$
have the same atomic type over
![]() $\mathfrak {A}$
. Since
$\mathfrak {A}$
. Since
![]() $\mathfrak {A}$
is homogeneous, it has quantifier elimination, and hence
$\mathfrak {A}$
is homogeneous, it has quantifier elimination, and hence
![]() $\vec {u}$
and
$\vec {u}$
and
![]() $\vec {v}$
have the same type over
$\vec {v}$
have the same type over
![]() $\mathfrak {A}$
.
$\mathfrak {A}$
.
(4)
![]() $\rightarrow $
(3). We show the contrapositive. Let us assume that item (3) does not hold. This means that
$\rightarrow $
(3). We show the contrapositive. Let us assume that item (3) does not hold. This means that
![]() $\mathfrak {A}$
has a relation R which is not quantifier-free definable over
$\mathfrak {A}$
has a relation R which is not quantifier-free definable over
![]() $\Delta _m(\mathfrak {A})$
. Then there exist tuples
$\Delta _m(\mathfrak {A})$
. Then there exist tuples
![]() $\vec {u}\in R, \vec {v}\in \bar {R}$
such that for every relation S of
$\vec {u}\in R, \vec {v}\in \bar {R}$
such that for every relation S of
![]() $\Delta _m(\mathfrak {A})$
, and
$\Delta _m(\mathfrak {A})$
, and
![]() $\pi \colon m\rightarrow n$
we have
$\pi \colon m\rightarrow n$
we have
![]() $\vec {u}_{\pi }\in S$
if and only if
$\vec {u}_{\pi }\in S$
if and only if
![]() $\vec {v}_{\pi }\in S$
. By definition this implies that for all
$\vec {v}_{\pi }\in S$
. By definition this implies that for all
![]() $\pi \colon m\rightarrow n$
the tuples
$\pi \colon m\rightarrow n$
the tuples
![]() $\vec {u}_{\pi }$
and
$\vec {u}_{\pi }$
and
![]() $\vec {v}_{\pi }$
have the same type over
$\vec {v}_{\pi }$
have the same type over
![]() $\mathfrak {A}$
. Thus the tuples
$\mathfrak {A}$
. Thus the tuples
![]() $\vec {u}$
and
$\vec {u}$
and
![]() $\vec {v}$
witness that Condition (4) fails.
$\vec {v}$
witness that Condition (4) fails.
The following is a direct consequence of Lemma 2.21.
Corollary 2.22. Let
![]() $\mathfrak {A}$
be an
$\mathfrak {A}$
be an
![]() $\omega $
-categorical structure. Then the following are equivalent:
$\omega $
-categorical structure. Then the following are equivalent:
-
(1)
 $\mathfrak {A}\in \mathcal {FH}$
.
$\mathfrak {A}\in \mathcal {FH}$
. -
(2)
 $\mathfrak {A}$
is interdefinable with
$\mathfrak {A}$
is interdefinable with
 $\Delta _m(\mathfrak {A})$
for some m.
$\Delta _m(\mathfrak {A})$
for some m. -
(3) There exists an
 $m\in \omega $
such that for all
$m\in \omega $
such that for all
 $\vec {u},\vec {v}\in A^n$
if
$\vec {u},\vec {v}\in A^n$
if
 $\vec {u}\not \approx _{\mathfrak {A}}\vec {v}$
then there exists a function
$\vec {u}\not \approx _{\mathfrak {A}}\vec {v}$
then there exists a function
 $\pi \colon m\rightarrow n$
such that
$\pi \colon m\rightarrow n$
such that
 $\vec {u}_{\pi }\not \approx _{\mathfrak {A}}\vec {v}_{\pi }$
.
$\vec {u}_{\pi }\not \approx _{\mathfrak {A}}\vec {v}_{\pi }$
.
2.8. Finite boundedness
In the study of homogeneous structures with a finite relational signature we are particularly interested in the ones which are also finitely bounded.
Definition 2.23. Let
![]() $\tau $
be a relational signature, and let
$\tau $
be a relational signature, and let
![]() $\mathcal {C}$
be a set of finite
$\mathcal {C}$
be a set of finite
![]() $\tau $
-structures. Then we denote by
$\tau $
-structures. Then we denote by
![]() $\operatorname {Forb}(\mathcal {C})$
the class of those finite
$\operatorname {Forb}(\mathcal {C})$
the class of those finite
![]() $\tau $
-structures which do not embed any structure from
$\tau $
-structures which do not embed any structure from
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
For a relational structure
![]() $\mathfrak {A}$
we call the class of finite structures which embed into
$\mathfrak {A}$
we call the class of finite structures which embed into
![]() $\mathfrak {A}$
the age of
$\mathfrak {A}$
the age of
![]() $\mathfrak {A}$
, and we denote this class by
$\mathfrak {A}$
, and we denote this class by
![]() $\operatorname {Age}(\mathfrak {A})$
.
$\operatorname {Age}(\mathfrak {A})$
.
A relational structure
![]() $\mathfrak {A}$
is called finitely bounded if its signature
$\mathfrak {A}$
is called finitely bounded if its signature
![]() $\tau :=\Sigma (\mathfrak {A})$
is finite, and there is finite set
$\tau :=\Sigma (\mathfrak {A})$
is finite, and there is finite set
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\tau $
-structures such that
$\tau $
-structures such that
![]() $\operatorname {Age}(\mathfrak {A})=\operatorname {Forb}(\mathcal {C})$
.
$\operatorname {Age}(\mathfrak {A})=\operatorname {Forb}(\mathcal {C})$
.
Next we give a couple of equivalent conditions for a homogeneous structure with a finite relational signature to be finitely bounded which we will need later.
Notation 2.24. Let
![]() $\mathcal {C}$
be a class of finite
$\mathcal {C}$
be a class of finite
![]() $\tau $
-structures. Then:
$\tau $
-structures. Then:
-
• We denote by
 ${\mathcal {C}}^{c}$
the class of those finite
${\mathcal {C}}^{c}$
the class of those finite
 $\tau $
-structures which are not in
$\tau $
-structures which are not in
 $\mathcal {C}$
.
$\mathcal {C}$
. -
• We denote by
 $\operatorname {Min}(\mathcal {C})$
the class of minimal structures in
$\operatorname {Min}(\mathcal {C})$
the class of minimal structures in
 $\mathcal {C}$
, i.e., the class of those structures in
$\mathcal {C}$
, i.e., the class of those structures in
 $\mathcal {C}$
which do not have a proper substructure which is also in
$\mathcal {C}$
which do not have a proper substructure which is also in
 $\mathcal {C}$
.
$\mathcal {C}$
.
Lemma 2.25. Let
![]() $\mathfrak {A}$
be a structure with a finite relational signature
$\mathfrak {A}$
be a structure with a finite relational signature
![]() $\tau $
. Then the following are equivalent:
$\tau $
. Then the following are equivalent:
-
(1)
 $\mathfrak {A}$
is finitely bounded.
$\mathfrak {A}$
is finitely bounded. -
(2)
 $\operatorname {Min}({\operatorname {Age}(\mathfrak {A})}^{c})$
contains finitely many structures up to isomorphism.
$\operatorname {Min}({\operatorname {Age}(\mathfrak {A})}^{c})$
contains finitely many structures up to isomorphism. -
(3) There exists some m such that the size of every structure in
 $\operatorname {Min}({\operatorname {Age}(\mathfrak {A})}^{c})$
is at most m.
$\operatorname {Min}({\operatorname {Age}(\mathfrak {A})}^{c})$
is at most m.
Proof The equivalence of conditions (2) and (3) is clear since
![]() $\tau $
is finite.
$\tau $
is finite.
(2)
![]() $\rightarrow $
(1). Let
$\rightarrow $
(1). Let
![]() $\mathcal {F}$
be a finite subset of
$\mathcal {F}$
be a finite subset of
![]() $\operatorname {Min}({\operatorname {Age}(\mathfrak {A})}^{c})$
so that every structure in
$\operatorname {Min}({\operatorname {Age}(\mathfrak {A})}^{c})$
so that every structure in
![]() $\operatorname {Min}({\operatorname {Age}(\mathfrak {A})}^{c})$
is represented in
$\operatorname {Min}({\operatorname {Age}(\mathfrak {A})}^{c})$
is represented in
![]() $\mathcal {F}$
. We claim that
$\mathcal {F}$
. We claim that
![]() $\operatorname {Age}(\mathfrak {A})=\operatorname {Forb}(\mathcal {F})$
. Let us suppose that
$\operatorname {Age}(\mathfrak {A})=\operatorname {Forb}(\mathcal {F})$
. Let us suppose that
![]() $\mathfrak {B}$
is a finite
$\mathfrak {B}$
is a finite
![]() $\tau $
-structure not contained in
$\tau $
-structure not contained in
![]() $\operatorname {Forb}(\mathcal {F})$
. Then
$\operatorname {Forb}(\mathcal {F})$
. Then
![]() $\mathfrak {B}$
has a substructure
$\mathfrak {B}$
has a substructure
![]() $\mathfrak {B}'$
which is isomorphic to some structure in
$\mathfrak {B}'$
which is isomorphic to some structure in
![]() $\mathcal {F}$
. In particular
$\mathcal {F}$
. In particular
![]() $\mathfrak {B}'\not \in \operatorname {Age}(\mathfrak {A})$
. Since
$\mathfrak {B}'\not \in \operatorname {Age}(\mathfrak {A})$
. Since
![]() $\operatorname {Age}(\mathfrak {A})$
is closed under taking substructures it follows that
$\operatorname {Age}(\mathfrak {A})$
is closed under taking substructures it follows that
![]() $\mathfrak {B}\not \in \operatorname {Age}(\mathfrak {A})$
. For the other direction let us assume that
$\mathfrak {B}\not \in \operatorname {Age}(\mathfrak {A})$
. For the other direction let us assume that
![]() $\mathfrak {B}\not \in \operatorname {Age}(\mathfrak {A})$
. Then
$\mathfrak {B}\not \in \operatorname {Age}(\mathfrak {A})$
. Then
![]() $\mathfrak {B}$
contains a minimal structure with this property, say
$\mathfrak {B}$
contains a minimal structure with this property, say
![]() $\mathfrak {B}'$
. Then by definition
$\mathfrak {B}'$
. Then by definition
![]() $\mathfrak {B}'$
is isomorphic to some structure in
$\mathfrak {B}'$
is isomorphic to some structure in
![]() $\mathfrak {C}\in \mathcal {F}$
, and hence
$\mathfrak {C}\in \mathcal {F}$
, and hence
![]() $\mathfrak {C}$
embeds into
$\mathfrak {C}$
embeds into
![]() $\mathfrak {B}$
, that is
$\mathfrak {B}$
, that is
![]() $\mathfrak {B}\not \in \operatorname {Forb}(\mathcal {F})$
.
$\mathfrak {B}\not \in \operatorname {Forb}(\mathcal {F})$
.
(1)
![]() $\rightarrow $
(3). Let us assume that
$\rightarrow $
(3). Let us assume that
![]() $\operatorname {Age}(\mathfrak {A})=\operatorname {Forb}(\mathcal {F})$
for some finite set
$\operatorname {Age}(\mathfrak {A})=\operatorname {Forb}(\mathcal {F})$
for some finite set
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() $\tau $
-structures, and let m be the maximum of the sizes of structures in
$\tau $
-structures, and let m be the maximum of the sizes of structures in
![]() $\mathcal {F}$
. Let
$\mathcal {F}$
. Let
![]() $\mathfrak {B}\in \operatorname {Min}({\operatorname {Age}(\mathfrak {A})}^{c})$
. Since
$\mathfrak {B}\in \operatorname {Min}({\operatorname {Age}(\mathfrak {A})}^{c})$
. Since
![]() $\mathfrak {B}\not \in \operatorname {Age}(\mathfrak {A})=\operatorname {Forb}(\mathcal {F})$
it follows
$\mathfrak {B}\not \in \operatorname {Age}(\mathfrak {A})=\operatorname {Forb}(\mathcal {F})$
it follows
![]() $\mathfrak {B}$
has a substructure
$\mathfrak {B}$
has a substructure
![]() $\mathfrak {B}'$
which is isomorphic to some
$\mathfrak {B}'$
which is isomorphic to some
![]() $\mathfrak {C}\in \mathcal {F}$
. But in this case
$\mathfrak {C}\in \mathcal {F}$
. But in this case
![]() $\mathfrak {B}'$
is also not in
$\mathfrak {B}'$
is also not in
![]() $\operatorname {Age}(\mathfrak {A})$
. Then the minimality of
$\operatorname {Age}(\mathfrak {A})$
. Then the minimality of
![]() $\mathfrak {B}$
implies that in fact
$\mathfrak {B}$
implies that in fact
![]() $\mathfrak {B}=\mathfrak {B}'$
, and hence
$\mathfrak {B}=\mathfrak {B}'$
, and hence
![]() $|\mathfrak {B}|\leq m$
.
$|\mathfrak {B}|\leq m$
.
Notation 2.26. For a structure
![]() $\mathfrak {A}$
we denote by
$\mathfrak {A}$
we denote by
![]() $b(\mathfrak {A})$
the maximum of
$b(\mathfrak {A})$
the maximum of
![]() $m(\mathfrak {A})$
(see Notation 2.6) and the maximum of sizes of structures in
$m(\mathfrak {A})$
(see Notation 2.6) and the maximum of sizes of structures in
![]() $\operatorname {Min}({\operatorname {Age}(\mathfrak {A})}^{c})$
.
$\operatorname {Min}({\operatorname {Age}(\mathfrak {A})}^{c})$
.
![]() $b(\mathfrak {A})$
is defined to be
$b(\mathfrak {A})$
is defined to be
![]() $\infty $
if such a maximum does not exist.
$\infty $
if such a maximum does not exist.
Lemma 2.25 shows that if
![]() $\mathfrak {A}$
is homogeneous then it is finitely bounded if and only if
$\mathfrak {A}$
is homogeneous then it is finitely bounded if and only if
![]() $b(\mathfrak {A})$
is finite.
$b(\mathfrak {A})$
is finite.
Notation 2.27. We denote by
![]() $\mathcal {FBH}$
the class of those structures which are interdefinable with a finitely bounded homogeneous relational structure.
$\mathcal {FBH}$
the class of those structures which are interdefinable with a finitely bounded homogeneous relational structure.
We can argue the same way as in the previous section that the structures in
![]() $\mathcal {FBH}$
can be described in terms of their automorphisms. In this case, however, we do not know of any nice such description. Nevertheless we know that the class
$\mathcal {FBH}$
can be described in terms of their automorphisms. In this case, however, we do not know of any nice such description. Nevertheless we know that the class
![]() $\{\operatorname {Aut}(\mathfrak {A})\colon \mathfrak {A}\in \mathcal {FBH}\}$
is closed under taking finite direct products, infinite copies, and rather surprisingly (as we will see in Section 4) it is also closed under taking finite index supergroups.
$\{\operatorname {Aut}(\mathfrak {A})\colon \mathfrak {A}\in \mathcal {FBH}\}$
is closed under taking finite direct products, infinite copies, and rather surprisingly (as we will see in Section 4) it is also closed under taking finite index supergroups.
2.9. Unions and copies of structures
Let us consider the following two constructions on structures.
Definition 2.28. Let
![]() $\mathfrak {A}_1,\dots ,\mathfrak {A}_n$
be relational structures with pairwise disjoint domains.
$\mathfrak {A}_1,\dots ,\mathfrak {A}_n$
be relational structures with pairwise disjoint domains.
Then we define the disjoint union
![]() $\mathfrak {B}$
of the structures
$\mathfrak {B}$
of the structures
![]() $\mathfrak {A}_1,\dots ,\mathfrak {A}_n$
, denoted by
$\mathfrak {A}_1,\dots ,\mathfrak {A}_n$
, denoted by
![]() $\biguplus _{i=1}^n\mathfrak {A}_i$
such that:
$\biguplus _{i=1}^n\mathfrak {A}_i$
such that:
-
• the domain set of
 $\mathfrak {B}$
is
$\mathfrak {B}$
is
 $\bigcup _{i=1}^nA_i$
,
$\bigcup _{i=1}^nA_i$
, -
• its signature is
 $\bigcup _{i=1}^n\Sigma (\mathfrak {A}_i)$
together with some pairwise different unary symbols
$\bigcup _{i=1}^n\Sigma (\mathfrak {A}_i)$
together with some pairwise different unary symbols
 $U_1,\dots ,U_n\not \in \bigcup _{i=1}^n\Sigma (\mathfrak {A}_i)$
,
$U_1,\dots ,U_n\not \in \bigcup _{i=1}^n\Sigma (\mathfrak {A}_i)$
, -
•
 $U_i^{\mathfrak {B}}=A_i$
for all
$U_i^{\mathfrak {B}}=A_i$
for all
 $1\leq i\leq n$
, and
$1\leq i\leq n$
, and -
•
 $R^{\mathfrak {B}}=R^{\mathfrak {A}_i}$
for all
$R^{\mathfrak {B}}=R^{\mathfrak {A}_i}$
for all
 $R\in \Sigma (\mathfrak {A}_i)$
.
$R\in \Sigma (\mathfrak {A}_i)$
.
Definition 2.29. Let
![]() $\mathfrak {A}$
be a relational structure. Then we define the structure
$\mathfrak {A}$
be a relational structure. Then we define the structure
![]() $\mathfrak {A}\wr \omega $
, called infinitely many copies of
$\mathfrak {A}\wr \omega $
, called infinitely many copies of
![]() $\mathfrak {A}$
, as follows.
$\mathfrak {A}$
, as follows.
-
• The domain set of
 $\mathfrak {A}\wr \omega $
is
$\mathfrak {A}\wr \omega $
is
 $A\times \omega $
.
$A\times \omega $
. -
• Its signature is
 $\Sigma (\mathfrak {A})\cup \{E\}$
where E is a binary relational symbol not contained in
$\Sigma (\mathfrak {A})\cup \{E\}$
where E is a binary relational symbol not contained in
 $\Sigma (\mathfrak {A})$
.
$\Sigma (\mathfrak {A})$
. -
•
 $E^{\mathfrak {A}\wr \omega }=\{((a_1,n),(a_2,n))\colon a_1,a_2\in A, n\in \omega \}$
.
$E^{\mathfrak {A}\wr \omega }=\{((a_1,n),(a_2,n))\colon a_1,a_2\in A, n\in \omega \}$
. -
•
 $R^{\mathfrak {A}\wr \omega }=\{((a_1,n),\dots ,(a_k,n))\colon (a_1,\dots ,a_k)\in R^{\mathfrak {A}}, n\in \omega \}$
for all
$R^{\mathfrak {A}\wr \omega }=\{((a_1,n),\dots ,(a_k,n))\colon (a_1,\dots ,a_k)\in R^{\mathfrak {A}}, n\in \omega \}$
for all
 $R\in \Sigma (\mathfrak {A})$
of arity k.
$R\in \Sigma (\mathfrak {A})$
of arity k.
The following two propositions are easy consequences of the definitions above.
Proposition 2.30. Let
![]() $\mathfrak {A}_1,\dots ,\mathfrak {A}_n$
be relational structures as in Definition 2.28. Then
$\mathfrak {A}_1,\dots ,\mathfrak {A}_n$
be relational structures as in Definition 2.28. Then
![]() $\operatorname {Aut}(\biguplus _{i=1}^n\mathfrak {A}_i)=\prod _{i=1}^n\operatorname {Aut}(\mathfrak {A}_i)$
.
$\operatorname {Aut}(\biguplus _{i=1}^n\mathfrak {A}_i)=\prod _{i=1}^n\operatorname {Aut}(\mathfrak {A}_i)$
.
Proposition 2.31. Let
![]() $\mathfrak {A}$
be a relational structure. Then
$\mathfrak {A}$
be a relational structure. Then
![]() $\operatorname {Aut}(\mathfrak {A}\wr \omega )=\operatorname {Aut}(\mathfrak {A})\wr \operatorname {Sym}(\omega )$
.
$\operatorname {Aut}(\mathfrak {A}\wr \omega )=\operatorname {Aut}(\mathfrak {A})\wr \operatorname {Sym}(\omega )$
.
The following two lemmas play a crucial role in our proofs later.
Lemma 2.32. Let
![]() $\mathfrak {A}_1,\dots ,\mathfrak {A}_n$
be structures with pairwise disjoint domains, and let
$\mathfrak {A}_1,\dots ,\mathfrak {A}_n$
be structures with pairwise disjoint domains, and let
![]() $\mathfrak {A}:=\prod _{i=1}^n\mathfrak {A}_i$
. Then:
$\mathfrak {A}:=\prod _{i=1}^n\mathfrak {A}_i$
. Then:
-
(1) if
 $\mathfrak {A}_1,\dots ,\mathfrak {A}_n$
are all homogeneous, then so is
$\mathfrak {A}_1,\dots ,\mathfrak {A}_n$
are all homogeneous, then so is
 $\mathfrak {A}$
, and
$\mathfrak {A}$
, and -
(2) if
 $\mathfrak {A}_1,\dots ,\mathfrak {A}_n$
are all finitely bounded, then so is
$\mathfrak {A}_1,\dots ,\mathfrak {A}_n$
are all finitely bounded, then so is
 $\mathfrak {A}$
.
$\mathfrak {A}$
.
Lemma 2.33. Let
![]() $\mathfrak {A}$
be homogeneous structures. Then
$\mathfrak {A}$
be homogeneous structures. Then
![]() $\mathfrak {A}\wr \omega $
is homogeneous, and
$\mathfrak {A}\wr \omega $
is homogeneous, and
![]() $\mathfrak {A}$
is finitely bounded, then so is
$\mathfrak {A}$
is finitely bounded, then so is
![]() $\mathfrak {A}\wr \omega $
.
$\mathfrak {A}\wr \omega $
.
Proof of Lemma 2.32
Item (1) follows from a straightforward induction using Lemma 3.1 in [Reference Bodirsky8].
As for item (2) let us assume that
![]() $\operatorname {Age}(\mathfrak {A})=\operatorname {Forb}(\mathcal {F}_i)$
for some finite sets of structures
$\operatorname {Age}(\mathfrak {A})=\operatorname {Forb}(\mathcal {F}_i)$
for some finite sets of structures
![]() $\mathcal {F}_i$
for
$\mathcal {F}_i$
for
![]() $1\leq i\leq n$
. For a
$1\leq i\leq n$
. For a
![]() $\Sigma (\mathfrak {A}_i)$
-structure
$\Sigma (\mathfrak {A}_i)$
-structure
![]() $\mathfrak {B}$
let
$\mathfrak {B}$
let
![]() $(\mathfrak {B};U_i)$
denote the structure
$(\mathfrak {B};U_i)$
denote the structure
![]() $\mathfrak {B}$
expanded by a unary relation denoted by
$\mathfrak {B}$
expanded by a unary relation denoted by
![]() $U_i$
which contains all elements of
$U_i$
which contains all elements of
![]() $B_i$
. Let
$B_i$
. Let
![]() $\mathcal {G}$
be the set of one-element
$\mathcal {G}$
be the set of one-element
![]() $\{U_1,\dots ,U_n\}$
-structures
$\{U_1,\dots ,U_n\}$
-structures
![]() $\mathfrak {B}$
such that either
$\mathfrak {B}$
such that either
![]() $\mathfrak {B}^{U_i}=\emptyset $
for all i or
$\mathfrak {B}^{U_i}=\emptyset $
for all i or
![]() $\mathfrak {B}^{U_i}=\mathfrak {B}^{U_j}=B$
for some
$\mathfrak {B}^{U_i}=\mathfrak {B}^{U_j}=B$
for some
![]() $i\neq j$
. Then it follows from the construction that
$i\neq j$
. Then it follows from the construction that
Therefore
![]() $\mathfrak {A}$
is finitely bounded.
$\mathfrak {A}$
is finitely bounded.
Proof of Lemma 2.33
Let us assume that the tuples
have the same quantifier-free type over
![]() $\mathfrak {A}\wr \omega $
. We have to show that
$\mathfrak {A}\wr \omega $
. We have to show that
![]() $\vec {u}$
and
$\vec {u}$
and
![]() $\vec {v}$
are in the same orbit of
$\vec {v}$
are in the same orbit of
![]() $\operatorname {Aut}(\mathfrak {A}\wr \omega )=\operatorname {Aut}(\mathfrak {A})\wr \operatorname {Sym}(\omega )$
. For an
$\operatorname {Aut}(\mathfrak {A}\wr \omega )=\operatorname {Aut}(\mathfrak {A})\wr \operatorname {Sym}(\omega )$
. For an
![]() $n\in \omega $
let us denote by
$n\in \omega $
let us denote by
![]() $\vec {u}_n$
(
$\vec {u}_n$
(
![]() $\vec {v}_n$
) the subtuple of
$\vec {v}_n$
) the subtuple of
![]() $\vec {u}$
(
$\vec {u}$
(
![]() $\vec {v}$
) containing those elements whose second coordinate is n. By definition it follows that
$\vec {v}$
) containing those elements whose second coordinate is n. By definition it follows that
![]() $m_i=m_j$
iff
$m_i=m_j$
iff
![]() $n_i=n_j$
for all
$n_i=n_j$
for all
![]() $1\leq i,j\leq k$
. Thus there exists a permutation
$1\leq i,j\leq k$
. Thus there exists a permutation
![]() $\sigma \in \operatorname {Sym}(\omega )$
such that for
$\sigma \in \operatorname {Sym}(\omega )$
such that for
![]() $\vec {u}_m:=((a_{i_1},m),\dots ,a_{i_k},m))$
we have
$\vec {u}_m:=((a_{i_1},m),\dots ,a_{i_k},m))$
we have
![]() $n_{i_1}=\dots =n_{i_k}=\sigma (m)$
. Moreover by the definition of
$n_{i_1}=\dots =n_{i_k}=\sigma (m)$
. Moreover by the definition of
![]() $\mathfrak {A}\wr \omega $
it follows that the tuples
$\mathfrak {A}\wr \omega $
it follows that the tuples
![]() $(a_{i_1},\dots ,a_{i_k})$
and
$(a_{i_1},\dots ,a_{i_k})$
and
![]() $(b_{i_1},\dots ,b_{i_k})$
have the same quantifier-free type in
$(b_{i_1},\dots ,b_{i_k})$
have the same quantifier-free type in
![]() $\mathfrak {A}$
. Thus by the homogeneity of
$\mathfrak {A}$
. Thus by the homogeneity of
![]() $\mathfrak {A}$
it follows that there exists some
$\mathfrak {A}$
it follows that there exists some
![]() $\alpha _m\in \operatorname {Aut}(\mathfrak {A})$
such that
$\alpha _m\in \operatorname {Aut}(\mathfrak {A})$
such that
![]() $\alpha _m(a_{i_j})=b_{i_j}$
for all
$\alpha _m(a_{i_j})=b_{i_j}$
for all
![]() $j=1,\dots ,k$
. Now let
$j=1,\dots ,k$
. Now let
![]() $\gamma \in \operatorname {Sym}(A\times \omega )$
be defined as
$\gamma \in \operatorname {Sym}(A\times \omega )$
be defined as ![]() . Then
. Then
![]() $\gamma \in \operatorname {Aut}(\mathfrak {A})\wr \operatorname {Sym}(\omega )$
and by our construction
$\gamma \in \operatorname {Aut}(\mathfrak {A})\wr \operatorname {Sym}(\omega )$
and by our construction
![]() $\gamma (a_i,m_i)=(\alpha _{m_i}(a_i),\beta (m_i))=(b_i,n_i)$
for all
$\gamma (a_i,m_i)=(\alpha _{m_i}(a_i),\beta (m_i))=(b_i,n_i)$
for all
![]() $1\leq i\leq k$
.
$1\leq i\leq k$
.
For the second part of the lemma let us assume that
![]() $\operatorname {Age}(\mathfrak {A})=\operatorname {Forb}(\mathcal {F})$
for some finite set of structures
$\operatorname {Age}(\mathfrak {A})=\operatorname {Forb}(\mathcal {F})$
for some finite set of structures
![]() $\mathcal {F}$
. Let
$\mathcal {F}$
. Let
![]() $\mathcal {G}_0$
be a finite set of structures in the signature
$\mathcal {G}_0$
be a finite set of structures in the signature
![]() $\{E\}$
so that
$\{E\}$
so that
![]() $\mathfrak {A}\in \operatorname {Forb}(\mathcal {G}_0)$
if and only if
$\mathfrak {A}\in \operatorname {Forb}(\mathcal {G}_0)$
if and only if
![]() $E^{\mathfrak {A}}$
is an equivalence relation on
$E^{\mathfrak {A}}$
is an equivalence relation on
![]() $\mathfrak {A}$
. We can do this by listing all three-element
$\mathfrak {A}$
. We can do this by listing all three-element
![]() $\{E\}$
-structures where E does not define an equivalence relation. For a
$\{E\}$
-structures where E does not define an equivalence relation. For a
![]() $\Sigma (\mathfrak {A})$
-structure
$\Sigma (\mathfrak {A})$
-structure
![]() $\mathfrak {C}$
let
$\mathfrak {C}$
let
![]() $\mathfrak {C}^*$
denote the structure
$\mathfrak {C}^*$
denote the structure
![]() $\mathfrak {C}$
expanded by a binary relation, denoted by E which contains every pair in
$\mathfrak {C}$
expanded by a binary relation, denoted by E which contains every pair in
![]() $C^2$
. Let
$C^2$
. Let
Then it is straightforward to check that
![]() $\operatorname {Forb}(\mathcal {G})$
is exactly the age of
$\operatorname {Forb}(\mathcal {G})$
is exactly the age of
![]() $\mathfrak {A}\wr \omega $
. Therefore
$\mathfrak {A}\wr \omega $
. Therefore
![]() $\mathfrak {A}\wr \omega $
is finitely bounded.
$\mathfrak {A}\wr \omega $
is finitely bounded.
Corollary 2.34. The classes
![]() $\mathcal {FH}$
and
$\mathcal {FH}$
and
![]() $\mathcal {FBH}$
are closed under taking finite disjoint unions and infinite copies.
$\mathcal {FBH}$
are closed under taking finite disjoint unions and infinite copies.
3. Hereditarily cellular structures
Definition 3.1. Let T be a complete theory in some language L. Then we say that T is monadically stable if every expansion of T by unary predicates is stable. A first-order structure
![]() $\mathfrak {A}$
is called monadically stable if its first-order theory is monadically stable.
$\mathfrak {A}$
is called monadically stable if its first-order theory is monadically stable.
We denote the class of countable
![]() $\omega $
-categorical monadically stable structures by
$\omega $
-categorical monadically stable structures by
![]() $\mathcal {M}$
. For a natural number k we denote by
$\mathcal {M}$
. For a natural number k we denote by
![]() $\mathcal {M}_k$
the class of structures in
$\mathcal {M}_k$
the class of structures in
![]() $\mathcal {M}$
whose Morley rank is at most k.
$\mathcal {M}$
whose Morley rank is at most k.
Lachlan showed in [Reference Lachlan34] that the structures in
![]() $\mathcal {M}$
can be described in terms of their automorphism group. For the description of these groups we first need a couple of definitions.
$\mathcal {M}$
can be described in terms of their automorphism group. For the description of these groups we first need a couple of definitions.
Definition 3.2. Let
![]() $G\leq \operatorname {Sym}(X)$
be a permutation group. Then a triple
$G\leq \operatorname {Sym}(X)$
be a permutation group. Then a triple
![]() $P=(K, \nabla , \Delta )$
is called an
$P=(K, \nabla , \Delta )$
is called an
![]() $\omega $
-partition of G iff:
$\omega $
-partition of G iff:
-
(1)
 $K\subset X$
is finite, and it is fixed setwise by G.
$K\subset X$
is finite, and it is fixed setwise by G. -
(2)
 $\Delta $
and
$\Delta $
and
 $\nabla $
are congruences of
$\nabla $
are congruences of
 $G|_{X\setminus K}$
with
$G|_{X\setminus K}$
with
 $\Delta \subset \nabla $
.
$\Delta \subset \nabla $
. -
(3)
 $\nabla $
has finitely many classes.
$\nabla $
has finitely many classes. -
(4) Every
 $\nabla $
-class is a union of
$\nabla $
-class is a union of
 $\aleph _0$
many
$\aleph _0$
many
 $\Delta $
-classes.
$\Delta $
-classes. -
(5) For every
 $C\in X/\nabla $
we have
$C\in X/\nabla $
we have
 $G_{((C))}/\Delta =\operatorname {Sym}(C/\Delta )$
.
$G_{((C))}/\Delta =\operatorname {Sym}(C/\Delta )$
.
The components of an
![]() $\omega $
-partition
$\omega $
-partition
![]() $P=(K, \nabla , \Delta )$
are the permutation groups
$P=(K, \nabla , \Delta )$
are the permutation groups
![]() $G_{((Y))}$
for all
$G_{((Y))}$
for all
![]() $Y\in X/\Delta $
.
$Y\in X/\Delta $
.
Remark 3.3. Definition 3.2 includes the case when
![]() $X=K$
. In this case
$X=K$
. In this case
![]() $\Delta =\nabla =\emptyset $
, and therefore all conditions (2)–(5) in Definition 3.2 are automatically satisfied.
$\Delta =\nabla =\emptyset $
, and therefore all conditions (2)–(5) in Definition 3.2 are automatically satisfied.
Definition 3.4. We define the classes of closed permutation groups
![]() $\mathcal {H}_{-1},\mathcal {H}_0,\mathcal {H}_1,\dots $
recursively as follows:
$\mathcal {H}_{-1},\mathcal {H}_0,\mathcal {H}_1,\dots $
recursively as follows:
-
•
 $\mathcal {H}_{-1}=\emptyset $
.
$\mathcal {H}_{-1}=\emptyset $
. -
• For
 $n\geq 0$
we define
$n\geq 0$
we define
 $G\in \mathcal {H}_n$
if and only if G has an
$G\in \mathcal {H}_n$
if and only if G has an
 $\omega $
-partition P so that every component of P is in
$\omega $
-partition P so that every component of P is in
 $\mathcal {H}_{n-1}$
.
$\mathcal {H}_{n-1}$
.
We define the class
![]() $\mathcal {H}$
as the union of all classes
$\mathcal {H}$
as the union of all classes
![]() $\mathcal {H}_n,\ n\in \omega $
. We call
$\mathcal {H}_n,\ n\in \omega $
. We call
![]() $\mathcal {H}$
the class of hereditarily
$\mathcal {H}$
the class of hereditarily
![]() $\omega $
-partitioned permutation groups. The rank of a hereditarily
$\omega $
-partitioned permutation groups. The rank of a hereditarily
![]() $\omega $
-partitioned group G, denoted by
$\omega $
-partitioned group G, denoted by
![]() $\operatorname {rk}(G)$
is the smallest n such that
$\operatorname {rk}(G)$
is the smallest n such that
![]() $G\in \mathcal {H}_n$
.
$G\in \mathcal {H}_n$
.
We say that a structure
![]() $\mathfrak {A}$
is hereditarily cellular if and only if
$\mathfrak {A}$
is hereditarily cellular if and only if
![]() $\operatorname {Aut}(\mathfrak {A})$
is hereditarily
$\operatorname {Aut}(\mathfrak {A})$
is hereditarily
![]() $\omega $
-partitioned.
$\omega $
-partitioned.
Remark 3.5. It is clear from the definition that
![]() $G\in \mathcal {H}_0$
if and only if
$G\in \mathcal {H}_0$
if and only if
![]() $X=K$
, i.e., when
$X=K$
, i.e., when
![]() $X=\operatorname {Dom}(G)$
is finite. Furthermore it can easily be shown by induction that
$X=\operatorname {Dom}(G)$
is finite. Furthermore it can easily be shown by induction that
![]() $\mathcal {H}_{n-1}\subset \mathcal {H}_n$
for all
$\mathcal {H}_{n-1}\subset \mathcal {H}_n$
for all
![]() $n\in \omega $
.
$n\in \omega $
.
Theorem 3.6 [Reference Lachlan34, Theorem 2.3]
![]() $\mathfrak {A}\in \mathcal {M}$
if and only if
$\mathfrak {A}\in \mathcal {M}$
if and only if
![]() $\mathfrak {A}$
is hereditarily cellular.
$\mathfrak {A}$
is hereditarily cellular.
There are two more facts from [Reference Lachlan34] that we need to keep in mind. We quote them below, slightly rephrased.
Proposition 3.7 [Reference Lachlan34, Proposition 1.4]
Let
![]() $(K, \nabla , \Delta )$
and
$(K, \nabla , \Delta )$
and
![]() $(K', \nabla ', \Delta ')$
be
$(K', \nabla ', \Delta ')$
be
![]() $\omega $
-partitions of a permutation group
$\omega $
-partitions of a permutation group
![]() $G\in \mathcal {H}$
. Then
$G\in \mathcal {H}$
. Then
![]() $K=K'$
,
$K=K'$
,
![]() $\nabla =\nabla '$
, and
$\nabla =\nabla '$
, and
![]() $\Delta =\Delta '$
.
$\Delta =\Delta '$
.
Proposition 3.8 [Reference Lachlan34, Propositions 1.3 and 1.6]
Let
![]() $\mathfrak {A}\in \mathcal {M}$
. Then
$\mathfrak {A}\in \mathcal {M}$
. Then
![]() $\mathfrak {A}$
is
$\mathfrak {A}$
is
![]() $\omega $
-stable, and its Morley rank is equal to
$\omega $
-stable, and its Morley rank is equal to
![]() $\operatorname {rk}(\operatorname {Aut}(\mathfrak {A}))$
.
$\operatorname {rk}(\operatorname {Aut}(\mathfrak {A}))$
.
By Proposition 3.7, the
![]() $\omega $
-partition witnessing
$\omega $
-partition witnessing
![]() $G\in \mathcal {H}$
is unique. Therefore from now on we will refer to this
$G\in \mathcal {H}$
is unique. Therefore from now on we will refer to this
![]() $\omega $
-partition as the
$\omega $
-partition as the
![]() $\omega $
-partition of the group G. Although our definition of the rank function
$\omega $
-partition of the group G. Although our definition of the rank function
![]() $\operatorname {rk}$
on
$\operatorname {rk}$
on
![]() $\mathcal {H}$
is different from the one given in [Reference Lachlan34] it is easy to see that the two definition are equivalent. Then by Proposition 1.4 in [Reference Lachlan34] we know that if
$\mathcal {H}$
is different from the one given in [Reference Lachlan34] it is easy to see that the two definition are equivalent. Then by Proposition 1.4 in [Reference Lachlan34] we know that if
![]() $\mathfrak {A}\in \mathcal {M}$
then
$\mathfrak {A}\in \mathcal {M}$
then
![]() $\operatorname {rk}(\operatorname {Aut}(\mathfrak {A}))$
is equal to the Morley rank of
$\operatorname {rk}(\operatorname {Aut}(\mathfrak {A}))$
is equal to the Morley rank of
![]() $\mathfrak {A}$
.
$\mathfrak {A}$
.
Corollary 3.9. Let
![]() $\mathfrak {A}$
be a structure. Then
$\mathfrak {A}$
be a structure. Then
![]() $\mathfrak {A}\in \mathcal {M}_n$
if and only if
$\mathfrak {A}\in \mathcal {M}_n$
if and only if
![]() $\operatorname {Aut}(\mathfrak {A})\in \mathcal {H}_n$
. In particular
$\operatorname {Aut}(\mathfrak {A})\in \mathcal {H}_n$
. In particular
![]() $\mathcal {M}=\bigcup _{n=0}^\infty \mathcal {M}_n$
, that is every structure in
$\mathcal {M}=\bigcup _{n=0}^\infty \mathcal {M}_n$
, that is every structure in
![]() $\mathcal {M}$
has a finite Morley rank.
$\mathcal {M}$
has a finite Morley rank.
Example 3.10. We define the structures
![]() $\mathcal {E}_n$
by recursion as follows.
$\mathcal {E}_n$
by recursion as follows.
![]() $\mathcal {E}_0$
is defined to be the one-element pure set, and
$\mathcal {E}_0$
is defined to be the one-element pure set, and
![]() $\mathcal {E}_n=\mathcal {E}_{n-1}\wr \omega $
. The structure
$\mathcal {E}_n=\mathcal {E}_{n-1}\wr \omega $
. The structure
![]() $\mathcal {E}_n$
can also be described as a countable infinite set A endowed with equivalence classes
$\mathcal {E}_n$
can also be described as a countable infinite set A endowed with equivalence classes
![]() $E_0\subsetneq \dots \subsetneq E_n$
such that:
$E_0\subsetneq \dots \subsetneq E_n$
such that:
-
•
 $E_0$
is the trivial equivalence relation,
$E_0$
is the trivial equivalence relation, -
•
 $E_n$
is the universal equivalence relation, and
$E_n$
is the universal equivalence relation, and -
• every
 $E_i$
class contains
$E_i$
class contains
 $\aleph _0$
many
$\aleph _0$
many
 $E_{i-1}$
classes for all
$E_{i-1}$
classes for all
 $1\leq i\leq n$
.
$1\leq i\leq n$
.
It is easy to see that
![]() $\mathcal {E}_n\in \mathcal {M}$
, and
$\mathcal {E}_n\in \mathcal {M}$
, and
![]() $\operatorname {rk}(\mathcal {E}_n)=n$
.
$\operatorname {rk}(\mathcal {E}_n)=n$
.
The class
![]() $\mathcal {M}$
can also be described by orbit growth on subsets. We say that a function
$\mathcal {M}$
can also be described by orbit growth on subsets. We say that a function
![]() $f\colon \omega \rightarrow \mathbb {R}$
is slower (faster) than exponential if for all real numbers
$f\colon \omega \rightarrow \mathbb {R}$
is slower (faster) than exponential if for all real numbers
![]() $c>1$
we have
$c>1$
we have
![]() $f(n)<c^n$
(
$f(n)<c^n$
(
![]() $f(n)>c^n$
) if n is large enough. Using these notions we know the following dichotomy for
$f(n)>c^n$
) if n is large enough. Using these notions we know the following dichotomy for
![]() $\omega $
-categorical stable structures.
$\omega $
-categorical stable structures.
Theorem 3.11 [Reference Braunfeld22, Theorem 1.1]
Let
![]() $\mathfrak {A}$
be an
$\mathfrak {A}$
be an
![]() $\omega $
-categorical stable structure. Then exactly one of the following holds:
$\omega $
-categorical stable structure. Then exactly one of the following holds:
-
(1)
 $o^s_n(\mathfrak {A})$
is slower than exponential, and
$o^s_n(\mathfrak {A})$
is slower than exponential, and
 $\mathfrak {A}$
is monadically stable.
$\mathfrak {A}$
is monadically stable. -
(2)
 $o^s_n(\mathfrak {A})$
is faster than exponential, and
$o^s_n(\mathfrak {A})$
is faster than exponential, and
 $\mathfrak {A}$
is not monadically stable.
$\mathfrak {A}$
is not monadically stable.
The following is a straightforward consequence of Theorem 3.11.
Theorem 3.12. Let
![]() $\mathfrak {A}$
be a structure. Then
$\mathfrak {A}$
be a structure. Then
![]() $\mathfrak {A}\in \mathcal {M}$
if and only if
$\mathfrak {A}\in \mathcal {M}$
if and only if
![]() $\mathfrak {A}$
is stable, and
$\mathfrak {A}$
is stable, and
![]() $o^s_n(\mathfrak {A})$
is slower than exponential.
$o^s_n(\mathfrak {A})$
is slower than exponential.
Note that if
![]() $\mathfrak {B}$
is a reduct of
$\mathfrak {B}$
is a reduct of
![]() $\mathfrak {A}$
then
$\mathfrak {A}$
then
![]() $o^s_n(\mathfrak {B})\leq o^s_n(\mathfrak {A})$
for all n. Therefore Theorem 3.12 immediately implies that the class
$o^s_n(\mathfrak {B})\leq o^s_n(\mathfrak {A})$
for all n. Therefore Theorem 3.12 immediately implies that the class
![]() $\mathcal {M}$
is closed under taking reducts. In fact one can arrive to the same conclusion directly from the definition. It is also clear that if
$\mathcal {M}$
is closed under taking reducts. In fact one can arrive to the same conclusion directly from the definition. It is also clear that if
![]() $\mathfrak {B}$
is a reduct of
$\mathfrak {B}$
is a reduct of
![]() $\mathfrak {A}$
then the Morley rank of
$\mathfrak {A}$
then the Morley rank of
![]() $\mathfrak {B}$
is at most the Morley rank of
$\mathfrak {B}$
is at most the Morley rank of
![]() $\mathfrak {A}$
. This implies that for all
$\mathfrak {A}$
. This implies that for all
![]() $n\in \omega $
the class
$n\in \omega $
the class
![]() $\mathcal {M}_n$
is also closed under taking reducts. In terms of permutation groups, this means that the classes
$\mathcal {M}_n$
is also closed under taking reducts. In terms of permutation groups, this means that the classes
![]() $\mathcal {H}_n,\ n\in \omega $
, and
$\mathcal {H}_n,\ n\in \omega $
, and
![]() $\mathcal {H}$
are closed under taking closed supergroups (see Theorem 2.13 and Corollary 3.9).
$\mathcal {H}$
are closed under taking closed supergroups (see Theorem 2.13 and Corollary 3.9).
We can also use Theorem 3.12 to show that the class
![]() $\mathcal {M}$
is closed under taking model-complete cores. As explained in the introduction this observation is particularly important in the study of CSPs.
$\mathcal {M}$
is closed under taking model-complete cores. As explained in the introduction this observation is particularly important in the study of CSPs.
Definition 3.13. An
![]() $\omega $
-categorical structure is called a model-complete core if the topological closure of
$\omega $
-categorical structure is called a model-complete core if the topological closure of
![]() $\operatorname {Aut}(\mathfrak {A})$
(in
$\operatorname {Aut}(\mathfrak {A})$
(in
![]() ${}^AA$
) is equal to the endomorphism monoid of
${}^AA$
) is equal to the endomorphism monoid of
![]() $\mathfrak {A}$
.
$\mathfrak {A}$
.
We say that two structures
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
are homomorphically equivalent if there exist homomorphisms
$\mathfrak {B}$
are homomorphically equivalent if there exist homomorphisms
![]() $f\colon \mathfrak {A}\rightarrow \mathfrak {B}$
and
$f\colon \mathfrak {A}\rightarrow \mathfrak {B}$
and
![]() $g\colon \mathfrak {B}\rightarrow \mathfrak {A}$
.
$g\colon \mathfrak {B}\rightarrow \mathfrak {A}$
.
Remark 3.14. As the name suggests a structure being a model-complete core is equivalent to it being model-complete and a core. However for our discussion we do not need to introduce these notion separately or in a more general context.
Theorem 3.15 ( [Reference Bodirsky6, Theorem 16])
Let
![]() $\mathfrak {A}$
be an
$\mathfrak {A}$
be an
![]() $\omega $
-categorical structure. Then
$\omega $
-categorical structure. Then
![]() $\mathfrak {A}$
is homomorphically equivalent to a model-complete core
$\mathfrak {A}$
is homomorphically equivalent to a model-complete core
![]() $\mathfrak {B}$
. Moreover the structure
$\mathfrak {B}$
. Moreover the structure
![]() $\mathfrak {B}$
is unique up to isomorphism, and it is again
$\mathfrak {B}$
is unique up to isomorphism, and it is again
![]() $\omega $
-categorical.
$\omega $
-categorical.
We call the (up to isomorphism) unique structure
![]() $\mathfrak {B}$
as in Theorem 3.15 the model-complete core of
$\mathfrak {B}$
as in Theorem 3.15 the model-complete core of
![]() $\mathfrak {A}$
.
$\mathfrak {A}$
.
Lemma 3.16. Let
![]() $\mathfrak {A}$
be an
$\mathfrak {A}$
be an
![]() $\omega $
-categorical structure, and let
$\omega $
-categorical structure, and let
![]() $\mathfrak {B}$
be its model-complete core. Then
$\mathfrak {B}$
be its model-complete core. Then
![]() $f_n(\mathfrak {B})\leq f_n(\mathfrak {A})$
for all
$f_n(\mathfrak {B})\leq f_n(\mathfrak {A})$
for all
![]() $n\in \omega $
where f is any of the operators
$n\in \omega $
where f is any of the operators
![]() $o,o^i$
, or
$o,o^i$
, or
![]() $o^s$
.
$o^s$
.
Proof The case when
![]() $f=o$
is shown in [Reference Bodirsky7]. The statement for
$f=o$
is shown in [Reference Bodirsky7]. The statement for
![]() $f=o^i$
and
$f=o^i$
and
![]() $f=o^s$
can be shown analogously.
$f=o^s$
can be shown analogously.
Combining Theorem 3.12 and Lemma 3.16 we obtain that the class
![]() $\mathcal {M}$
is closed under taking model-complete cores. By refining this argument one can also show that the same conclusion holds for all classes
$\mathcal {M}$
is closed under taking model-complete cores. By refining this argument one can also show that the same conclusion holds for all classes
![]() $\mathcal {M}_n,\ n\in \omega $
.
$\mathcal {M}_n,\ n\in \omega $
.
3.1. Building up the class
 $\mathcal {H}$
$\mathcal {H}$
In this section we construct recursively a subclass
![]() $\mathcal {H}'$
of
$\mathcal {H}'$
of
![]() $\mathcal {H}$
, and examine some properties of groups in
$\mathcal {H}$
, and examine some properties of groups in
![]() $\mathcal {H}'$
. Then in the next section we will show that in fact
$\mathcal {H}'$
. Then in the next section we will show that in fact
![]() $\mathcal {H}'=\mathcal {H}$
, and as a result we obtain an explicit recursive description of
$\mathcal {H}'=\mathcal {H}$
, and as a result we obtain an explicit recursive description of
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Lemma 3.17. Let H be a permutation group. Then the group ![]() has an
has an
![]() $\omega $
-partition with all components isomorphic to H.
$\omega $
-partition with all components isomorphic to H.
Proof Let ![]() and
and ![]() . Then
. Then ![]() is an
is an
![]() $\omega $
-partition of G with all components isomorphic to H.
$\omega $
-partition of G with all components isomorphic to H.
Corollary 3.18. If
![]() $H\in \mathcal {H}_n$
then
$H\in \mathcal {H}_n$
then
![]() $H\wr \operatorname {Sym}(\omega )\in \mathcal {H}_{n+1}$
.
$H\wr \operatorname {Sym}(\omega )\in \mathcal {H}_{n+1}$
.
The following lemma tells us that the classes
![]() $\mathcal {H}_n$
are closed under finite direct products.
$\mathcal {H}_n$
are closed under finite direct products.
Lemma 3.19. Let
![]() $H_1,\dots ,H_k\in \mathcal {H}_n$
with pairwise disjoint domains. Then
$H_1,\dots ,H_k\in \mathcal {H}_n$
with pairwise disjoint domains. Then ![]() .
.
Proof For
![]() $i=1,\dots ,k$
let
$i=1,\dots ,k$
let ![]() be the
be the
![]() $\omega $
-partition of
$\omega $
-partition of
![]() $H_i$
witnessing the fact that
$H_i$
witnessing the fact that
![]() $H_i\in \mathcal {H}_n$
, that is, every component of
$H_i\in \mathcal {H}_n$
, that is, every component of
![]() $P_i$
is in
$P_i$
is in
![]() $\mathcal {H}_{n-1}$
. Let
$\mathcal {H}_{n-1}$
. Let ![]() with
with ![]() and
and ![]() . We claim that P is an
. We claim that P is an
![]() $\omega $
-partition of H, and every component of P is a component of one of the
$\omega $
-partition of H, and every component of P is a component of one of the
![]() $\omega $
-partitions
$\omega $
-partitions
![]() $P_i$
with
$P_i$
with
![]() $i=1,\dots ,k$
. Since these components are all contained in
$i=1,\dots ,k$
. Since these components are all contained in
![]() $\mathcal {H}_{n-1}$
by our assumption, this implies the statement of the lemma.
$\mathcal {H}_{n-1}$
by our assumption, this implies the statement of the lemma.
It follows from the definition that H fixes the sets ![]() , and
, and
![]() $H|_{X_i}=H_i$
. This implies immediately that H fixes the set K and the equivalence relations
$H|_{X_i}=H_i$
. This implies immediately that H fixes the set K and the equivalence relations
![]() $\Delta $
and
$\Delta $
and
![]() $\nabla $
. It is clear from the definition that K is finite,
$\nabla $
. It is clear from the definition that K is finite,
![]() $\nabla $
has finitely many classes, and every
$\nabla $
has finitely many classes, and every
![]() $\nabla $
-class is a union of
$\nabla $
-class is a union of
![]() $\aleph _0$
many
$\aleph _0$
many
![]() $\Delta $
-classes. It remains to show that item (5) of Definition 3.2 holds for the congruences
$\Delta $
-classes. It remains to show that item (5) of Definition 3.2 holds for the congruences
![]() $\nabla $
and
$\nabla $
and
![]() $\Delta $
. Let C be a
$\Delta $
. Let C be a
![]() $\nabla $
-class. Then by definition C is also a
$\nabla $
-class. Then by definition C is also a
![]() $\nabla _i$
-class for some
$\nabla _i$
-class for some
![]() $1\leq i\leq k$
. Then we have
$1\leq i\leq k$
. Then we have
 $$ \begin{align*}H_{((C))}/\Delta=H_{((C))}/\Delta_i=(H|_{X_i})_{((C))}/\Delta_i=&\\(H_i)_{((C))}/\Delta_i=&\operatorname{Sym}(C/\Delta_i)=\operatorname{Sym}(C/\Delta), \end{align*} $$
$$ \begin{align*}H_{((C))}/\Delta=H_{((C))}/\Delta_i=(H|_{X_i})_{((C))}/\Delta_i=&\\(H_i)_{((C))}/\Delta_i=&\operatorname{Sym}(C/\Delta_i)=\operatorname{Sym}(C/\Delta), \end{align*} $$
where the second-to-last equality above follows from the assumption that
![]() $P_i$
is an
$P_i$
is an
![]() $\omega $
-partition. This finishes the proof that
$\omega $
-partition. This finishes the proof that
![]() $P=(K,\nabla ,\Delta )$
is an
$P=(K,\nabla ,\Delta )$
is an
![]() $\omega $
-partition. Now if X is a
$\omega $
-partition. Now if X is a
![]() $\Delta $
-class, then X is also a
$\Delta $
-class, then X is also a
![]() $\Delta _i$
-class for some
$\Delta _i$
-class for some
![]() $1\leq i\leq k$
, and thus
$1\leq i\leq k$
, and thus
![]() $H_{((Y))}=(H|_{X_i})_{((Y))}=(H_i)_{((Y))}$
which is by definition a component of
$H_{((Y))}=(H|_{X_i})_{((Y))}=(H_i)_{((Y))}$
which is by definition a component of
![]() $P_i$
. This shows that every component of P is a component of
$P_i$
. This shows that every component of P is a component of
![]() $P_i$
for some
$P_i$
for some
![]() $1\leq i \leq k$
.
$1\leq i \leq k$
.
In the next few paragraphs we will construct a structure with an
![]() $\omega $
-partition and dissect a permutation that preserves the equivalence relations on it. Our ultimate goal is to give an explicit description of the groups in
$\omega $
-partition and dissect a permutation that preserves the equivalence relations on it. Our ultimate goal is to give an explicit description of the groups in
![]() $\mathcal {H}$
and the structures in
$\mathcal {H}$
and the structures in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Now we fix some notational conventions that we will use throughout this section. First we fix some pairwise disjoint sets
![]() $Y_0,\ldots ,Y_k$
, with
$Y_0,\ldots ,Y_k$
, with
![]() $Y_0$
finite and all other
$Y_0$
finite and all other
![]() $Y_i$
nonempty; let
$Y_i$
nonempty; let ![]() . We define
. We define
![]() $i\colon Y\to \{0,\ldots ,k\}$
as the function mapping a to the unique j such that
$i\colon Y\to \{0,\ldots ,k\}$
as the function mapping a to the unique j such that
![]() $a\in Y_j$
. We will use
$a\in Y_j$
. We will use
![]() $\Omega (Y_0,\dots ,Y_k)$
to denote the set
$\Omega (Y_0,\dots ,Y_k)$
to denote the set
![]() $\bigcup _{i=1}^k(Y_i\times \omega )\cup Y_0\times \{0\}$
. Given
$\bigcup _{i=1}^k(Y_i\times \omega )\cup Y_0\times \{0\}$
. Given
![]() $u=(a,n)\in \Omega (Y_0,\dots ,Y_k)$
, we define
$u=(a,n)\in \Omega (Y_0,\dots ,Y_k)$
, we define
![]() $p(u)=a, q(u)=n$
.
$p(u)=a, q(u)=n$
.
Let

and

Observe that
![]() $Y_0\times \{0\}$
is the only finite
$Y_0\times \{0\}$
is the only finite
![]() $\nabla $
-class, so any permutation of
$\nabla $
-class, so any permutation of
![]() $\Omega (Y_0,\dots ,Y_k)$
that preserves
$\Omega (Y_0,\dots ,Y_k)$
that preserves
![]() $\nabla $
must stabilize
$\nabla $
must stabilize
![]() $Y_0\times \{0\}$
setwise.
$Y_0\times \{0\}$
setwise.
Suppose that
![]() $\sigma \in \operatorname {Sym}(\Omega (Y_0,\dots ,Y_k))$
preserves
$\sigma \in \operatorname {Sym}(\Omega (Y_0,\dots ,Y_k))$
preserves
![]() $\nabla $
and
$\nabla $
and
![]() $\Delta $
. We identify
$\Delta $
. We identify
![]() $\Omega (Y_0,\dots ,Y_k)/\nabla $
with
$\Omega (Y_0,\dots ,Y_k)/\nabla $
with
![]() $\{0,\ldots ,k\}$
via the mapping that sends
$\{0,\ldots ,k\}$
via the mapping that sends
![]() $Y_0\times \{0\}$
to 0 and
$Y_0\times \{0\}$
to 0 and
![]() $Y_i\times \omega $
to i, for
$Y_i\times \omega $
to i, for
![]() $1\leq i\leq k$
. Similarly,
$1\leq i\leq k$
. Similarly,
![]() $\Omega (Y_0,\dots ,Y_k)/\Delta $
is identified with
$\Omega (Y_0,\dots ,Y_k)/\Delta $
is identified with
![]() $\{(0,0)\}\cup \{1,\ldots ,k\}\times \omega $
. These identifications allow us to think of
$\{(0,0)\}\cup \{1,\ldots ,k\}\times \omega $
. These identifications allow us to think of
![]() $\sigma /\nabla $
as a permutation
$\sigma /\nabla $
as a permutation
![]() $\phi (\sigma )\in \operatorname {Sym}(\{0,\ldots ,k\})$
that fixes 0 and similarly
$\phi (\sigma )\in \operatorname {Sym}(\{0,\ldots ,k\})$
that fixes 0 and similarly
![]() $\sigma /\Delta $
as a permutation
$\sigma /\Delta $
as a permutation
![]() $\psi (\sigma )\in \operatorname {Sym}(\{(0,0)\}\cup \{1,\ldots ,k\}\times \omega )$
that fixes
$\psi (\sigma )\in \operatorname {Sym}(\{(0,0)\}\cup \{1,\ldots ,k\}\times \omega )$
that fixes
![]() $(0,0)$
.
$(0,0)$
.
We can further decompose
![]() $\psi (\sigma )$
into a constant mapping
$\psi (\sigma )$
into a constant mapping
![]() $\psi _0\equiv 0$
and k permutations of
$\psi _0\equiv 0$
and k permutations of
![]() $\omega $
, say
$\omega $
, say
![]() $\psi _i(\sigma )$
, so that
$\psi _i(\sigma )$
, so that
![]() $\psi (\sigma )(i,n)=(\phi (\sigma )(i),\psi _i(\sigma )(n))$
for all
$\psi (\sigma )(i,n)=(\phi (\sigma )(i),\psi _i(\sigma )(n))$
for all
![]() $(n,i)\in \{(0,0)\}\cup (\{1,\dots ,k\}\times \omega )$
. Thus
$(n,i)\in \{(0,0)\}\cup (\{1,\dots ,k\}\times \omega )$
. Thus
![]() $\psi (\sigma )$
is uniquely determined by the permutations
$\psi (\sigma )$
is uniquely determined by the permutations
![]() $\psi _i(\sigma )$
(
$\psi _i(\sigma )$
(
![]() $0\leq i \leq k$
) and
$0\leq i \leq k$
) and
![]() $\phi (\sigma )$
.
$\phi (\sigma )$
.
Given any
![]() $\vec {n}=(0,n_1,\ldots ,n_k)\in \{0\}\times \omega ^k$
, we define
$\vec {n}=(0,n_1,\ldots ,n_k)\in \{0\}\times \omega ^k$
, we define
![]() $\vec {\mathbf {n}}$
as
$\vec {\mathbf {n}}$
as
![]() $((0,0),(1,n_1),\ldots ,(k,n_k)) \in \{(0,0)\}\cup \{1,\ldots ,k\}\times \omega $
. For each
$((0,0),(1,n_1),\ldots ,(k,n_k)) \in \{(0,0)\}\cup \{1,\ldots ,k\}\times \omega $
. For each
![]() $\vec {n}$
we define an injection
$\vec {n}$
we define an injection
![]() $\ell _{\vec {n}}\colon Y\to \Omega (Y_0,\ldots ,Y_k)$
by putting
$\ell _{\vec {n}}\colon Y\to \Omega (Y_0,\ldots ,Y_k)$
by putting
![]() $\ell _{\vec {n}}(a)=(a,n_{i(a)})$
. We define
$\ell _{\vec {n}}(a)=(a,n_{i(a)})$
. We define
These functions are elements of
![]() $\operatorname {Sym}(Y)$
. For
$\operatorname {Sym}(Y)$
. For
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $i\in \{0,\ldots k\}$
we define
$i\in \{0,\ldots k\}$
we define
where
![]() $\mathbf {n}$
is the tuple
$\mathbf {n}$
is the tuple
![]() $(0,n,\ldots ,n)$
. Then
$(0,n,\ldots ,n)$
. Then
![]() $\rho _n^i(\sigma )$
is a bijection
$\rho _n^i(\sigma )$
is a bijection
![]() $Y_i\to Y_{\phi (\sigma )(i)}$
.
$Y_i\to Y_{\phi (\sigma )(i)}$
.
Let
![]() $\sigma \in \operatorname {Aut}(\Omega (Y_0,\dots ,Y_k);Y_0\times \{0\},\nabla ,\Delta )$
be arbitrary. Then using the notation above it follows that given
$\sigma \in \operatorname {Aut}(\Omega (Y_0,\dots ,Y_k);Y_0\times \{0\},\nabla ,\Delta )$
be arbitrary. Then using the notation above it follows that given
![]() $(a,n)\in \Omega (Y_0,\dots ,Y_k)$
we have
$(a,n)\in \Omega (Y_0,\dots ,Y_k)$
we have
![]() $\sigma ((a,n))=(\rho _n^{i(a)}(\sigma )(a),\psi _{i(a)}(\sigma )(n))$
. In particular a permutation
$\sigma ((a,n))=(\rho _n^{i(a)}(\sigma )(a),\psi _{i(a)}(\sigma )(n))$
. In particular a permutation
![]() $\sigma $
in
$\sigma $
in
![]() $\operatorname {Aut}(\Omega (Y_0,\dots ,Y_k);Y_0\times \{0\},\nabla ,\Delta )$
is uniquely determined by the maps
$\operatorname {Aut}(\Omega (Y_0,\dots ,Y_k);Y_0\times \{0\},\nabla ,\Delta )$
is uniquely determined by the maps
![]() $\rho _{n}^i(\sigma )$
and
$\rho _{n}^i(\sigma )$
and
![]() $\psi _i(\sigma )$
.
$\psi _i(\sigma )$
.
For a
![]() $\tau \in \{\operatorname {id}(\{(0,0)\})\}\times \operatorname {Sym}(\omega )^k$
we write
$\tau \in \{\operatorname {id}(\{(0,0)\})\}\times \operatorname {Sym}(\omega )^k$
we write
![]() $\hat {\tau }$
for the unique element in
$\hat {\tau }$
for the unique element in
![]() $\operatorname {Aut}(\Omega (Y_0,\dots ,Y_k);Y_0\times \{0\},\nabla ,\Delta )$
for which for all
$\operatorname {Aut}(\Omega (Y_0,\dots ,Y_k);Y_0\times \{0\},\nabla ,\Delta )$
for which for all
![]() $0\leq j\leq k$
we have
$0\leq j\leq k$
we have
![]() $\rho _n^j(\hat {\tau })=\operatorname {id}(Y_j)$
, and
$\rho _n^j(\hat {\tau })=\operatorname {id}(Y_j)$
, and
![]() $\psi (\hat {\tau })=\tau $
.
$\psi (\hat {\tau })=\tau $
.
Lemma 3.20. Let
![]() $\sigma ,\tau \in \operatorname {Aut}(\Omega (Y_0,\dots ,Y_k);Y_0\times \{0\},\nabla ,\Delta )$
. Then for all
$\sigma ,\tau \in \operatorname {Aut}(\Omega (Y_0,\dots ,Y_k);Y_0\times \{0\},\nabla ,\Delta )$
. Then for all
![]() $\vec {n}=(n_0,\dots ,n_k)\in \{0\}\times \omega ^k$
we have:
$\vec {n}=(n_0,\dots ,n_k)\in \{0\}\times \omega ^k$
we have:
-
(i)
 $\rho _{\vec {n}}(\tau \sigma )=\rho _{\psi (\sigma )(\vec {\mathbf {n}})}(\tau )\rho _{\vec {n}}(\sigma )$
, and
$\rho _{\vec {n}}(\tau \sigma )=\rho _{\psi (\sigma )(\vec {\mathbf {n}})}(\tau )\rho _{\vec {n}}(\sigma )$
, and -
(ii)
 $\rho _{\vec {n}}(\sigma ^{-1})=(\rho _{\psi (\sigma ^{-1})(\vec {\mathbf {n}})}(\sigma ))^{-1}$
.
$\rho _{\vec {n}}(\sigma ^{-1})=(\rho _{\psi (\sigma ^{-1})(\vec {\mathbf {n}})}(\sigma ))^{-1}$
.
Proof (i) Let
![]() $a\in Y_i$
. Then
$a\in Y_i$
. Then
![]() $\sigma $
maps
$\sigma $
maps
![]() $u=(a,n_i)$
to
$u=(a,n_i)$
to ![]() for
for
![]() $i'=i(\rho _{\vec {n}}(\sigma )(a))$
. By definition
$i'=i(\rho _{\vec {n}}(\sigma )(a))$
. By definition
![]() $p(\tau (u'))=\rho _{\psi (\sigma )(\vec {\mathbf {n}})}(\tau )(\rho _{\vec {n}}(\sigma )(a))$
. On the other hand
$p(\tau (u'))=\rho _{\psi (\sigma )(\vec {\mathbf {n}})}(\tau )(\rho _{\vec {n}}(\sigma )(a))$
. On the other hand
![]() $p(\tau (u'))=p(\tau \sigma (u))=\rho _{\vec {n}}(\tau \sigma )(a)$
. This shows the equality in item (i).
$p(\tau (u'))=p(\tau \sigma (u))=\rho _{\vec {n}}(\tau \sigma )(a)$
. This shows the equality in item (i).
(ii) Using item (i) it follows that
and the equality (ii) follows.
Suppose now that
![]() $N_0,\dots ,N_k$
are permutation groups with
$N_0,\dots ,N_k$
are permutation groups with
![]() $\operatorname {Dom}(N_i)=Y_i$
, and
$\operatorname {Dom}(N_i)=Y_i$
, and
![]() $N_0=\{\operatorname {id}(Y_0)\}$
, the trivial permutation group on
$N_0=\{\operatorname {id}(Y_0)\}$
, the trivial permutation group on
![]() $Y_0$
. (Recall that
$Y_0$
. (Recall that
![]() $Y_0$
is assumed to be finite.) We will use the notation N for the group
$Y_0$
is assumed to be finite.) We will use the notation N for the group
![]() $\prod _{i=0}^kN_i$
.
$\prod _{i=0}^kN_i$
.
Definition 3.21. Let H be a permutation group acting on Y such that N is a normal subgroup of H, and H fixes
![]() $Y_0$
setwise. Then we define the subset
$Y_0$
setwise. Then we define the subset
![]() $\mathcal {G}(H;N_0,\dots ,N_k)$
of
$\mathcal {G}(H;N_0,\dots ,N_k)$
of
![]() $\operatorname {Sym}(\Omega (Y_0,\dots ,Y_k))$
as follows. A permutation
$\operatorname {Sym}(\Omega (Y_0,\dots ,Y_k))$
as follows. A permutation
![]() $\sigma $
is contained in
$\sigma $
is contained in
![]() $\mathcal {G}(H;N_0,\dots ,N_k)$
if and only if:
$\mathcal {G}(H;N_0,\dots ,N_k)$
if and only if:
-
(a)
 $\sigma $
fixes
$\sigma $
fixes
 $Y_0\times \{0\}$
setwise,
$Y_0\times \{0\}$
setwise, -
(b)
 $\sigma $
preserves the relations
$\sigma $
preserves the relations
 $\nabla $
and
$\nabla $
and
 $\Delta $
,
$\Delta $
, -
(c) for all
 $\vec {n}=(n_0,n_1,\dots ,n_k)\in \{0\}\times \omega ^k$
it holds that
$\vec {n}=(n_0,n_1,\dots ,n_k)\in \{0\}\times \omega ^k$
it holds that
 $\rho _{\vec {n}}(\sigma )\in H$
, and
$\rho _{\vec {n}}(\sigma )\in H$
, and -
(d) for all
 $\vec {n},\vec {m}\in \{0\}\times \omega ^k$
the maps
$\vec {n},\vec {m}\in \{0\}\times \omega ^k$
the maps
 $\rho _{\vec {n}}(\sigma )$
and
$\rho _{\vec {n}}(\sigma )$
and
 $\rho _{\vec {m}}(\sigma )$
are equal modulo N.
$\rho _{\vec {m}}(\sigma )$
are equal modulo N.
Define

It is a straightforward consequence of the definition that
![]() $\mathcal {G}(N;N_0,\dots ,N_k)=\mathcal {N}(N_0,\dots ,N_k)$
, and if
$\mathcal {G}(N;N_0,\dots ,N_k)=\mathcal {N}(N_0,\dots ,N_k)$
, and if
![]() $H\leq H'$
then
$H\leq H'$
then
![]() $\mathcal {G}(H;N_0,\dots ,N_k)\subset \mathcal {G}(H';N_0,\dots ,N_k)$
(assuming that both sides are defined).
$\mathcal {G}(H;N_0,\dots ,N_k)\subset \mathcal {G}(H';N_0,\dots ,N_k)$
(assuming that both sides are defined).
Lemma 3.22.
![]() $\mathcal {G}(H;N_0,\dots ,N_k)$
is a subgroup of
$\mathcal {G}(H;N_0,\dots ,N_k)$
is a subgroup of
![]() $\operatorname {Sym}(\Omega (Y_0,\dots ,Y_k))$
.
$\operatorname {Sym}(\Omega (Y_0,\dots ,Y_k))$
.
Proof Let
![]() $\sigma ,\tau $
be permutations in
$\sigma ,\tau $
be permutations in
![]() $\operatorname {Sym}(\Omega (Y_0,\dots ,Y_k))$
satisfying conditions (a)–(d) in Definition 3.21. We have to show that the permutation
$\operatorname {Sym}(\Omega (Y_0,\dots ,Y_k))$
satisfying conditions (a)–(d) in Definition 3.21. We have to show that the permutation
![]() $\sigma \tau ^{-1}$
also satisfies conditions (a)–(d). For conditions (a) and (b) this is obvious.
$\sigma \tau ^{-1}$
also satisfies conditions (a)–(d). For conditions (a) and (b) this is obvious.
For condition (c) let
![]() $\vec {n}\in \{0\}\times \omega ^k$
be arbitrary. Then by Lemma 3.20 we have
$\vec {n}\in \{0\}\times \omega ^k$
be arbitrary. Then by Lemma 3.20 we have
For condition (d) let
![]() $\vec {n},\vec {m}\in \{0\}\times \omega ^k$
. Then we have
$\vec {n},\vec {m}\in \{0\}\times \omega ^k$
. Then we have
 $$ \begin{align*} \rho_{\vec{n}}(\sigma\tau^{-1})&= \rho_{\psi(\tau^{-1})(\vec{\mathbf{n}})}(\sigma)(\rho_{\psi(\tau^{-1})(\vec{\mathbf{n}})}(\tau))^{-1}\\ &\equiv\rho_{\psi(\tau^{-1})(\vec{\mathbf{m}})}(\sigma)(\rho_{\psi(\tau^{-1})(\vec{\mathbf{m}})}(\tau))^{-1}=\rho_{\vec{n}}(\sigma\tau^{-1}) \pmod{N}.\\[-34pt] \end{align*} $$
$$ \begin{align*} \rho_{\vec{n}}(\sigma\tau^{-1})&= \rho_{\psi(\tau^{-1})(\vec{\mathbf{n}})}(\sigma)(\rho_{\psi(\tau^{-1})(\vec{\mathbf{n}})}(\tau))^{-1}\\ &\equiv\rho_{\psi(\tau^{-1})(\vec{\mathbf{m}})}(\sigma)(\rho_{\psi(\tau^{-1})(\vec{\mathbf{m}})}(\tau))^{-1}=\rho_{\vec{n}}(\sigma\tau^{-1}) \pmod{N}.\\[-34pt] \end{align*} $$
We next show that the group
![]() $\mathcal {N}(N_0,\dots ,N_k)$
has no nontrivial closed oligomorphic normal subgroup.
$\mathcal {N}(N_0,\dots ,N_k)$
has no nontrivial closed oligomorphic normal subgroup.
Lemma 3.23. Suppose
![]() $G\leq \operatorname {Sym}(X)$
is a closed oligomorphic permutation group and let K be a nontrivial closed oligomorphic normal subgroup of G. Then G has a nontrivial closed normal subgroup of finite index.
$G\leq \operatorname {Sym}(X)$
is a closed oligomorphic permutation group and let K be a nontrivial closed oligomorphic normal subgroup of G. Then G has a nontrivial closed normal subgroup of finite index.
Proof Since K is closed, and
![]() $K\subsetneq G$
, we can pick a natural number n such that K has more n-orbits than G. We claim that the n-orbits of K give a G-invariant partition of X. Indeed, suppose that
$K\subsetneq G$
, we can pick a natural number n such that K has more n-orbits than G. We claim that the n-orbits of K give a G-invariant partition of X. Indeed, suppose that
![]() $\vec {u}$
and
$\vec {u}$
and
![]() $\vec {v}$
are in the same n-orbit of K, that is
$\vec {v}$
are in the same n-orbit of K, that is
![]() $\vec {v}\in K(\vec {u})$
. Then for any
$\vec {v}\in K(\vec {u})$
. Then for any
![]() $\alpha \in G$
we have
$\alpha \in G$
we have
Since K is oligomorphic this partition has finitely many parts. Thus, the stabilizer of this partition is a closed finite-index normal subgroup of G. By the choice of n this stabilizer is different from G.
Lemma 3.24. Suppose
![]() $K\leq \operatorname {Sym}(Y)$
and
$K\leq \operatorname {Sym}(Y)$
and
![]() $S\leq \operatorname {Sym}(\omega )$
are closed permutation groups, and S is transitive and has no proper closed subgroup of finite index. Then
$S\leq \operatorname {Sym}(\omega )$
are closed permutation groups, and S is transitive and has no proper closed subgroup of finite index. Then
![]() $K\wr S$
has no non-trivial closed normal subgroup of finite index.
$K\wr S$
has no non-trivial closed normal subgroup of finite index.
Proof For the ease of notation we identify S with the subgroup
![]() $\{\operatorname {id}(\operatorname {Dom}(K))\}\wr S$
.
$\{\operatorname {id}(\operatorname {Dom}(K))\}\wr S$
.
Let G be a finite-index closed normal subgroup of
![]() $K\wr S$
. Then
$K\wr S$
. Then
![]() $G\geq S$
by our assumption on S. Let
$G\geq S$
by our assumption on S. Let ![]() . We have to show that
. We have to show that
![]() $Q=K^\omega $
. Note that Q is closed normal subgroup of
$Q=K^\omega $
. Note that Q is closed normal subgroup of
![]() $K^\omega $
, so S acts continuously on
$K^\omega $
, so S acts continuously on
![]() $K^\omega /Q$
by conjugation. Moreover, the index
$K^\omega /Q$
by conjugation. Moreover, the index
![]() $|K^\omega :Q|=|L:G|$
is finite; therefore, the kernel of this action is a closed subgroup of S of finite index which must equal S by our assumption. This implies that for all
$|K^\omega :Q|=|L:G|$
is finite; therefore, the kernel of this action is a closed subgroup of S of finite index which must equal S by our assumption. This implies that for all
![]() $g\in S$
and
$g\in S$
and
![]() $p\in K^\omega $
the commutator
$p\in K^\omega $
the commutator
![]() $[g,p]$
is contained in Q.
$[g,p]$
is contained in Q.
Now let
![]() $k\in K$
be arbitrary, and write
$k\in K$
be arbitrary, and write
![]() $p=(k,\operatorname {id},\operatorname {id},\dots )$
. By the transitivity of S we know that for all
$p=(k,\operatorname {id},\operatorname {id},\dots )$
. By the transitivity of S we know that for all
![]() $n\in \omega $
there exists some
$n\in \omega $
there exists some
![]() $g_n\in S$
such that
$g_n\in S$
such that
![]() $g_n(0)=n$
. Then
$g_n(0)=n$
. Then
![]() $q_n=[g_n,p]=(k,\operatorname {id},\dots ,\operatorname {id},k^{-1},\operatorname {id},\dots )\in Q$
where the
$q_n=[g_n,p]=(k,\operatorname {id},\dots ,\operatorname {id},k^{-1},\operatorname {id},\dots )\in Q$
where the
![]() $k^{-1}$
appears in position n. The limit of the sequence
$k^{-1}$
appears in position n. The limit of the sequence
![]() $(q_n)_n$
as
$(q_n)_n$
as
![]() $n\rightarrow \infty $
is p. As Q is closed, we obtain
$n\rightarrow \infty $
is p. As Q is closed, we obtain
![]() $p\in Q$
. The elements
$p\in Q$
. The elements
![]() $(k,\operatorname {id},\operatorname {id},\dots )$
with
$(k,\operatorname {id},\operatorname {id},\dots )$
with
![]() $k\in K$
, however, together with S, generate a dense subgroup of
$k\in K$
, however, together with S, generate a dense subgroup of
![]() $K^\omega $
. Since Q is closed, this means that in fact
$K^\omega $
. Since Q is closed, this means that in fact
![]() $Q=K^\omega $
.
$Q=K^\omega $
.
Lemma 3.25. The group
![]() $\mathcal {N}(N_0,\dots ,N_k)$
has no nontrivial closed oligomorphic normal subgroup.
$\mathcal {N}(N_0,\dots ,N_k)$
has no nontrivial closed oligomorphic normal subgroup.
Proof Recall that

where
![]() $L_0=\{\operatorname {id}(Y_0\times \{0\})\}$
and
$L_0=\{\operatorname {id}(Y_0\times \{0\})\}$
and
![]() $L_i=N_i\wr \operatorname {Sym}(\omega )$
for
$L_i=N_i\wr \operatorname {Sym}(\omega )$
for
![]() $1\leq i\geq k$
. Let
$1\leq i\geq k$
. Let
We have to show that
![]() $G_i=L_i$
for all
$G_i=L_i$
for all
![]() $i\in \{0,\dots ,k\}$
. For
$i\in \{0,\dots ,k\}$
. For
![]() $i=0$
there is nothing to prove. Otherwise,
$i=0$
there is nothing to prove. Otherwise,
![]() $G_i$
is a closed oligomorphic normal subgroup of
$G_i$
is a closed oligomorphic normal subgroup of
![]() $L_i$
, and the equality follows from Lemmas 3.23 and 3.24.
$L_i$
, and the equality follows from Lemmas 3.23 and 3.24.
Lemma 3.26. The group
![]() $\mathcal {N}(N_0,\dots ,N_k)$
is a normal subgroup of
$\mathcal {N}(N_0,\dots ,N_k)$
is a normal subgroup of
![]() $\mathcal {G}(H;N_0,\dots ,N_k)$
, and
$\mathcal {G}(H;N_0,\dots ,N_k)$
, and
![]() $\mathcal {G}(H;N_0,\dots ,N_k)/\mathcal {N}(N_0,\dots ,N_k)\simeq H/N$
.
$\mathcal {G}(H;N_0,\dots ,N_k)/\mathcal {N}(N_0,\dots ,N_k)\simeq H/N$
.
Proof Condition (d) says that for a permutation
![]() $\sigma \in \mathcal {G}(H;N_0,\dots ,N_k)$
all the permutations of the form
$\sigma \in \mathcal {G}(H;N_0,\dots ,N_k)$
all the permutations of the form
![]() $\rho _{\vec {n}}(\sigma )$
are the same modulo N. Then we define
$\rho _{\vec {n}}(\sigma )$
are the same modulo N. Then we define
![]() $\varphi (\sigma )$
to be the coset of N containing all these elements. Then
$\varphi (\sigma )$
to be the coset of N containing all these elements. Then
![]() $\varphi $
defines a homomorphism from
$\varphi $
defines a homomorphism from
![]() $\mathcal {G}(H;N_0,\dots ,N_k)$
to
$\mathcal {G}(H;N_0,\dots ,N_k)$
to
![]() $H/N$
, and the kernel of this homomorphism is
$H/N$
, and the kernel of this homomorphism is
![]() $\mathcal {N}(N_0,\dots ,N_k)$
. Note also that
$\mathcal {N}(N_0,\dots ,N_k)$
. Note also that
![]() $\varphi $
is surjective. Indeed, for an
$\varphi $
is surjective. Indeed, for an
![]() $h\in H$
let us denote by
$h\in H$
let us denote by
![]() $h^*$
the permutation
$h^*$
the permutation
![]() $(a,n)\mapsto (h(a),n)$
. Then clearly
$(a,n)\mapsto (h(a),n)$
. Then clearly
![]() $\varphi (h^*)=h$
. The statement of the lemma then follows from the first isomorphism theorem.
$\varphi (h^*)=h$
. The statement of the lemma then follows from the first isomorphism theorem.
Lemma 3.27. Let
![]() $G\subset \operatorname {Sym}(\Omega (Y_0,\ldots ,Y_k))$
be a closed permutation group which preserves the set
$G\subset \operatorname {Sym}(\Omega (Y_0,\ldots ,Y_k))$
be a closed permutation group which preserves the set
![]() $Y_0\times \{0\}$
and the equivalence relations
$Y_0\times \{0\}$
and the equivalence relations
![]() $\Delta $
and
$\Delta $
and
![]() $\nabla $
. Let us assume moreover that
$\nabla $
. Let us assume moreover that
![]() $\mathcal {N}(N_0,\dots ,N_k)\leq G$
, and for all
$\mathcal {N}(N_0,\dots ,N_k)\leq G$
, and for all
![]() $i=1,\dots ,k$
we have
$i=1,\dots ,k$
we have
![]() $G_{((Y_i\times \{0\}))}=N_i\times \{\operatorname {id}(\{0\})\}$
. Then for all
$G_{((Y_i\times \{0\}))}=N_i\times \{\operatorname {id}(\{0\})\}$
. Then for all
![]() $\vec {n},\vec {m}\in \{0\}\times \omega ^k$
and
$\vec {n},\vec {m}\in \{0\}\times \omega ^k$
and
![]() $\sigma \in G$
the permutations
$\sigma \in G$
the permutations
![]() $\rho _{\vec {n}}(\sigma )$
and
$\rho _{\vec {n}}(\sigma )$
and
![]() $\rho _{\vec {m}}(\sigma )$
are equal modulo N.
$\rho _{\vec {m}}(\sigma )$
are equal modulo N.
Proof It is enough to show the statement of the lemma for
![]() $\vec {m}=\vec {0}=(0,\dots ,0)$
and any
$\vec {m}=\vec {0}=(0,\dots ,0)$
and any
![]() $\vec {n}=(n_0,\dots ,n_k)$
. By definition both
$\vec {n}=(n_0,\dots ,n_k)$
. By definition both
![]() $\rho _{\vec {0}}$
and
$\rho _{\vec {0}}$
and
![]() $\rho _{\vec {n}}$
map
$\rho _{\vec {n}}$
map
![]() $Y_i$
to
$Y_i$
to
![]() $Y_{\phi (\sigma )(i)}$
. Therefore
$Y_{\phi (\sigma )(i)}$
. Therefore ![]() fixes the sets
fixes the sets
![]() $Y_0,\dots ,Y_k$
setwise.
$Y_0,\dots ,Y_k$
setwise.
Now let ![]() . We have to show that
. We have to show that
![]() $\tau _i\in N_i$
. If
$\tau _i\in N_i$
. If
![]() $n_i=0$
, then there is nothing to prove. Otherwise, let
$n_i=0$
, then there is nothing to prove. Otherwise, let
![]() $\nu \in \{\operatorname {id}(\{(0,0)\})\}\times \operatorname {Sym}(\omega )^k$
which flips
$\nu \in \{\operatorname {id}(\{(0,0)\})\}\times \operatorname {Sym}(\omega )^k$
which flips
![]() $(0,i)$
and
$(0,i)$
and
![]() $(n,i)$
and fixes everything else. Then we have
$(n,i)$
and fixes everything else. Then we have
![]() $\hat {\nu }\in \mathcal {N}(N_0,\dots ,N_k)\subseteq G$
. Now let
$\hat {\nu }\in \mathcal {N}(N_0,\dots ,N_k)\subseteq G$
. Now let ![]() . Then
. Then
![]() $\mu $
fixes every element outside
$\mu $
fixes every element outside
![]() $Y_i\times \{0,n\}$
, and by Lemma 3.20 we have
$Y_i\times \{0,n\}$
, and by Lemma 3.20 we have
 $$ \begin{align*} \rho_0^i(\mu)&=\rho_0^i(\hat{\nu}^{-1}\sigma^{-1}\hat{\nu}\sigma)\\ &=(\rho_{\psi_i(\hat{\nu}^{-1}\sigma^{-1}\hat{\nu}\sigma)(0)}^i(\hat{\nu}))^{-1}(\rho_{\psi_i(\sigma^{-1}\hat{\nu}\sigma)(0)}^i(\sigma))^{-1}\rho_{\psi_i(\sigma)(0)}^i(\hat{\nu})\rho_0^i(\sigma)\\ &=(\rho_n^i(\sigma))^{-1}\rho_0^i(\sigma)=\tau_i. \end{align*} $$
$$ \begin{align*} \rho_0^i(\mu)&=\rho_0^i(\hat{\nu}^{-1}\sigma^{-1}\hat{\nu}\sigma)\\ &=(\rho_{\psi_i(\hat{\nu}^{-1}\sigma^{-1}\hat{\nu}\sigma)(0)}^i(\hat{\nu}))^{-1}(\rho_{\psi_i(\sigma^{-1}\hat{\nu}\sigma)(0)}^i(\sigma))^{-1}\rho_{\psi_i(\sigma)(0)}^i(\hat{\nu})\rho_0^i(\sigma)\\ &=(\rho_n^i(\sigma))^{-1}\rho_0^i(\sigma)=\tau_i. \end{align*} $$
Now by conjugating
![]() $\sigma '$
by the permutation
$\sigma '$
by the permutation
![]() $\widehat {\nu _{n'}}$
where
$\widehat {\nu _{n'}}$
where
![]() $\nu _{n'}$
denotes the transposition
$\nu _{n'}$
denotes the transposition
![]() $((i,n)\,(i,n'))$
we obtain that for all
$((i,n)\,(i,n'))$
we obtain that for all
![]() $n'\in \omega $
there exists a permutation
$n'\in \omega $
there exists a permutation
![]() $\mu ^{\prime }_{n'}$
in G such that
$\mu ^{\prime }_{n'}$
in G such that
![]() $\rho _0^i(\mu _{n^{\prime \prime }})=\tau _i$
, and
$\rho _0^i(\mu _{n^{\prime \prime }})=\tau _i$
, and
![]() $\mu ^{\prime }_{n'}$
fixes every element outside
$\mu ^{\prime }_{n'}$
fixes every element outside
![]() $Y_i\times \{0,n'\}$
. Since G is closed this implies that G contains a permutation
$Y_i\times \{0,n'\}$
. Since G is closed this implies that G contains a permutation
![]() $\mu '$
such that
$\mu '$
such that
![]() $\rho _0^i(\mu ')=\tau $
and
$\rho _0^i(\mu ')=\tau $
and
![]() $\mu '$
fixes every element outside
$\mu '$
fixes every element outside
![]() $Y_i\times \{0\}$
. Then the permutation
$Y_i\times \{0\}$
. Then the permutation
![]() $(\tau _i,\operatorname {id}(\{0\}))$
is contained in
$(\tau _i,\operatorname {id}(\{0\}))$
is contained in
![]() $G_{(((Y_i\times \{0\}))}=N_i\times \{\operatorname {id}(\{0\})\}$
, and thus
$G_{(((Y_i\times \{0\}))}=N_i\times \{\operatorname {id}(\{0\})\}$
, and thus
![]() $\tau _i\in N_i$
, and this is what we wanted to show.
$\tau _i\in N_i$
, and this is what we wanted to show.
Lemma 3.28. Let G be as in Lemma 3.27, and let ![]() . Then
. Then
![]() $N\triangleleft H$
.
$N\triangleleft H$
.
Proof Let
![]() $\sigma \in N$
,
$\sigma \in N$
,
![]() $\tau \in H$
. We have to show that
$\tau \in H$
. We have to show that
![]() $\tau ^{-1}\sigma \tau \in N$
. Let
$\tau ^{-1}\sigma \tau \in N$
. Let
![]() $\sigma _0$
be the permutation of
$\sigma _0$
be the permutation of
![]() $\Omega (Y_0,\dots ,Y_k)$
which maps
$\Omega (Y_0,\dots ,Y_k)$
which maps
![]() $(a,0)$
to
$(a,0)$
to
![]() $(\sigma (a),0)$
for all
$(\sigma (a),0)$
for all
![]() $a\in Y$
, and fixes every other element. Then by definition
$a\in Y$
, and fixes every other element. Then by definition
![]() $\sigma _0\in \mathcal {N}(N_0,\dots ,N_k)\subset G$
. Let
$\sigma _0\in \mathcal {N}(N_0,\dots ,N_k)\subset G$
. Let
![]() $\tilde {\tau }\in G$
so that
$\tilde {\tau }\in G$
so that
![]() $\rho _{\vec {0}}(\tilde {\tau })=\tau $
. Then by permuting the
$\rho _{\vec {0}}(\tilde {\tau })=\tau $
. Then by permuting the
![]() $\Delta $
classes of
$\Delta $
classes of
![]() $\Omega (Y_0,\dots ,Y_k)$
with elements
$\Omega (Y_0,\dots ,Y_k)$
with elements
![]() $\{\hat {\nu }: \nu \in \{\operatorname {id}(\{(0,0)\})\}\times \operatorname {Sym}(\omega )^k\}$
we can assume without loss of generality that
$\{\hat {\nu }: \nu \in \{\operatorname {id}(\{(0,0)\})\}\times \operatorname {Sym}(\omega )^k\}$
we can assume without loss of generality that
![]() $\psi (\tilde {\tau })$
fixes all
$\psi (\tilde {\tau })$
fixes all
![]() $(0,i)$
with
$(0,i)$
with
![]() $i=0,\dots ,k$
. In this case the permutation
$i=0,\dots ,k$
. In this case the permutation
![]() $\sigma _0':=\tilde {\tau }^{-1}\sigma _0\tilde {\tau }\in G$
fixes every element outside
$\sigma _0':=\tilde {\tau }^{-1}\sigma _0\tilde {\tau }\in G$
fixes every element outside
![]() $\bigcup _{i=0}^kY_i\times \{0\}$
, and by Lemma 3.20 we have
$\bigcup _{i=0}^kY_i\times \{0\}$
, and by Lemma 3.20 we have
This implies that
![]() $\tau ^{-1}\sigma \tau \in N$
.
$\tau ^{-1}\sigma \tau \in N$
.
Lemma 3.29. Let
![]() $G_1$
and
$G_1$
and
![]() $G_2$
be as in Lemma 3.27, and let
$G_2$
be as in Lemma 3.27, and let ![]() for
for
![]() $i=1,2$
. If
$i=1,2$
. If
![]() $H_1=H_2$
, then
$H_1=H_2$
, then
![]() $G_1=G_2$
.
$G_1=G_2$
.
Proof It follows from our conditions that the groups
![]() $G_1$
and
$G_1$
and
![]() $G_2$
both contain the group
$G_2$
both contain the group
![]() $\mathcal {N}(N_0,\dots ,N_k)=\{\operatorname {id}(Y_0\times \{0\})\}\times \prod _{i=1}^k(N_i\wr \operatorname {Sym}(\omega ))$
.
$\mathcal {N}(N_0,\dots ,N_k)=\{\operatorname {id}(Y_0\times \{0\})\}\times \prod _{i=1}^k(N_i\wr \operatorname {Sym}(\omega ))$
.
Lemma 3.27 implies that for all
![]() $\sigma \in G_1$
the coset
$\sigma \in G_1$
the coset
![]() $\rho _{\vec {n}}(\sigma )N$
does not depend on
$\rho _{\vec {n}}(\sigma )N$
does not depend on
![]() $\vec {n}$
. Let us denote this coset by
$\vec {n}$
. Let us denote this coset by
![]() $h(\sigma )$
. By Lemma 3.28 we know that N is a normal subgroup of
$h(\sigma )$
. By Lemma 3.28 we know that N is a normal subgroup of
![]() $H_1$
. Then it follows easily from Lemma 3.20 that h defines a homomorphism from
$H_1$
. Then it follows easily from Lemma 3.20 that h defines a homomorphism from
![]() $G_1$
to
$G_1$
to
![]() $H_1/N$
, and the kernel of h is exactly
$H_1/N$
, and the kernel of h is exactly
![]() $\mathcal {N}(N_0,\dots ,N_k)$
.
$\mathcal {N}(N_0,\dots ,N_k)$
.
Using this if
![]() $\sigma \in G_1$
then by definition it follows that
$\sigma \in G_1$
then by definition it follows that
![]() $\rho _{\vec {0}}(\sigma ')=\rho _{\vec {0}}(\sigma )$
for some
$\rho _{\vec {0}}(\sigma ')=\rho _{\vec {0}}(\sigma )$
for some
![]() $\sigma '\in G_2$
. This implies
$\sigma '\in G_2$
. This implies
![]() $h(\sigma )=h(\sigma ')$
, and thus
$h(\sigma )=h(\sigma ')$
, and thus
![]() $h(\sigma (\sigma ')^{-1})=h(\sigma )(h(\sigma '))^{-1}=\operatorname {id}$
, that is
$h(\sigma (\sigma ')^{-1})=h(\sigma )(h(\sigma '))^{-1}=\operatorname {id}$
, that is
![]() $\rho _{\vec {n}}(\sigma (\sigma ')^{-1})$
for all
$\rho _{\vec {n}}(\sigma (\sigma ')^{-1})$
for all
![]() $\vec {n}\in \{0\}\times \omega ^k$
. This means exactly that
$\vec {n}\in \{0\}\times \omega ^k$
. This means exactly that
![]() $\sigma (\sigma ')^{-1}\in \mathcal {N}(N_0,\dots ,N_k)$
. Therefore
$\sigma (\sigma ')^{-1}\in \mathcal {N}(N_0,\dots ,N_k)$
. Therefore
![]() $\sigma =(\sigma (\sigma ')^{-1})\sigma '\in \mathcal {N}(N_0,\dots ,N_k)G_2=G_2$
. Hence
$\sigma =(\sigma (\sigma ')^{-1})\sigma '\in \mathcal {N}(N_0,\dots ,N_k)G_2=G_2$
. Hence
![]() $G_1\subset G_2$
. The other inclusion follows analogously.
$G_1\subset G_2$
. The other inclusion follows analogously.
Lemma 3.30. Let G be as in Lemma 3.27. Then there exists a permutation group H acting on Y which normalizes N, and such that
![]() $G=\mathcal {G}(H;N_0,\dots ,N_k)$
.
$G=\mathcal {G}(H;N_0,\dots ,N_k)$
.
Proof Let ![]() . By Lemma 3.29 we already know that H normalizes N. Let
. By Lemma 3.29 we already know that H normalizes N. Let
![]() $G_1=G, G_2=\mathcal {G}(H;N_0,\dots ,N_k)$
, and
$G_1=G, G_2=\mathcal {G}(H;N_0,\dots ,N_k)$
, and
![]() $H_2=\{\rho _{\vec {0}}(\sigma )\colon \sigma \in G_2\}$
. Then
$H_2=\{\rho _{\vec {0}}(\sigma )\colon \sigma \in G_2\}$
. Then
![]() $H_2=H=H_1$
, and thus Lemma 3.29 implies
$H_2=H=H_1$
, and thus Lemma 3.29 implies
![]() $G=G_1=G_2=\mathcal {G}(H;N_0,\dots ,N_k)$
.
$G=G_1=G_2=\mathcal {G}(H;N_0,\dots ,N_k)$
.
Definition 3.31. We define the classes of permutation groups
![]() $\mathcal {H}_{-1}',\mathcal {H}_0',\mathcal {H}_1',\dots $
recursively as follows:
$\mathcal {H}_{-1}',\mathcal {H}_0',\mathcal {H}_1',\dots $
recursively as follows:
-
•
 $\mathcal {H}_{-1}'=\emptyset $
.
$\mathcal {H}_{-1}'=\emptyset $
. -
• For
 $n\geq 0$
we define
$n\geq 0$
we define
 $G\in \mathcal {H}_n'$
if and only if there exist
$G\in \mathcal {H}_n'$
if and only if there exist
 $N_0,\dots ,N_k,N,H$
as in Definition 3.21 such that
$N_0,\dots ,N_k,N,H$
as in Definition 3.21 such that
 $N_1,\dots ,N_k,H\in \mathcal {H}_{n-1}'$
and G is isomorphic to
$N_1,\dots ,N_k,H\in \mathcal {H}_{n-1}'$
and G is isomorphic to
 $\mathcal {G}(H;N_0,\dots ,N_k)$
.
$\mathcal {G}(H;N_0,\dots ,N_k)$
.
We define
![]() $\mathcal {H}'$
as the union of all classes
$\mathcal {H}'$
as the union of all classes
![]() $\mathcal {H}_n'\colon n\in \omega $
.
$\mathcal {H}_n'\colon n\in \omega $
.
Remark 3.32. Later we will see that in fact the classes
![]() $\mathcal {H}_n'$
are closed under finite direct products. Therefore we could drop the assumption that
$\mathcal {H}_n'$
are closed under finite direct products. Therefore we could drop the assumption that
![]() $N\in \mathcal {H}_{n-1}'$
in the recursion. This fact can also be derived from the definition directly. We will also see that we can drop the condition
$N\in \mathcal {H}_{n-1}'$
in the recursion. This fact can also be derived from the definition directly. We will also see that we can drop the condition
![]() $H\in \mathcal {H}_{n-1}'$
as well.
$H\in \mathcal {H}_{n-1}'$
as well.
Lemma 3.33. Every group in
![]() $\mathcal {H}'$
is oligomorphic.
$\mathcal {H}'$
is oligomorphic.
Proof We show that every group in
![]() $\mathcal {H}_n'$
is oligomorphic by induction on n. For
$\mathcal {H}_n'$
is oligomorphic by induction on n. For
![]() $n=-1$
there is nothing to show. For the induction step let us assume that
$n=-1$
there is nothing to show. For the induction step let us assume that
![]() $G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some
$G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some
![]() $H,N_0,\dots ,N_k\in \mathcal {H}_{n-1}'$
. Then
$H,N_0,\dots ,N_k\in \mathcal {H}_{n-1}'$
. Then
![]() $G\geq \mathcal {N}(N_0,\dots ,N_k)$
. By item (ii) of Lemma 2.4 we know that the groups
$G\geq \mathcal {N}(N_0,\dots ,N_k)$
. By item (ii) of Lemma 2.4 we know that the groups
![]() $N_i\wr \operatorname {Sym}(\omega ),\ 1\leq i \leq k$
are oligomorphic. By the discussion in Section 2.4 we know that finite direct products of oligomorphic groups are oligomorphic. Therefore, the group
$N_i\wr \operatorname {Sym}(\omega ),\ 1\leq i \leq k$
are oligomorphic. By the discussion in Section 2.4 we know that finite direct products of oligomorphic groups are oligomorphic. Therefore, the group
![]() $\mathcal {N}(N_0,\dots ,N_k)=\{\operatorname {id}(Y_0\times \{0\})\}\times \prod _{i=1}^k(N_i\wr \operatorname {Sym}(\omega ))$
is oligomorphic. Hence G is also oligomorphic.
$\mathcal {N}(N_0,\dots ,N_k)=\{\operatorname {id}(Y_0\times \{0\})\}\times \prod _{i=1}^k(N_i\wr \operatorname {Sym}(\omega ))$
is oligomorphic. Hence G is also oligomorphic.
Lemma 3.34. Let
![]() $G\in \mathcal {H}'$
. Then G has finitely many closed normal subgroups contained in
$G\in \mathcal {H}'$
. Then G has finitely many closed normal subgroups contained in
![]() $\mathcal {H}'$
, and all of these have a finite index in G.
$\mathcal {H}'$
, and all of these have a finite index in G.
Proof We show the statement of the lemma for
![]() $\mathcal {H}_n'$
by induction on n. For
$\mathcal {H}_n'$
by induction on n. For
![]() $n=-1$
there is nothing to show. For the induction step let us assume that
$n=-1$
there is nothing to show. For the induction step let us assume that
![]() $G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some
$G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some
![]() $H,N_0,\dots ,N_k,N=\prod _{i=0}^kN_i\in \mathcal {H}_{n-1}'$
. By Lemma 3.26 it follows that
$H,N_0,\dots ,N_k,N=\prod _{i=0}^kN_i\in \mathcal {H}_{n-1}'$
. By Lemma 3.26 it follows that
![]() $|G:\mathcal {N}(N_0,\dots ,N_k)|=|H:N|$
. By definition N is a normal subgroup of
$|G:\mathcal {N}(N_0,\dots ,N_k)|=|H:N|$
. By definition N is a normal subgroup of
![]() $H\in \mathcal {H}_{n-1}'$
. Since
$H\in \mathcal {H}_{n-1}'$
. Since
![]() $N,H\in \mathcal {H}_{n-1}$
this implies that
$N,H\in \mathcal {H}_{n-1}$
this implies that
![]() $|H:N|$
is finite by the induction hypothesis. Therefore
$|H:N|$
is finite by the induction hypothesis. Therefore
![]() $|G:\mathcal {N}(N_0,\dots ,N_k)|$
is finite. Now let
$|G:\mathcal {N}(N_0,\dots ,N_k)|$
is finite. Now let
![]() $G_1\in \mathcal {H}'$
be a closed normal subgroup of G. By Lemma 3.33 we know that
$G_1\in \mathcal {H}'$
be a closed normal subgroup of G. By Lemma 3.33 we know that
![]() $G_1$
is oligomorphic. Let
$G_1$
is oligomorphic. Let ![]() . Then by the second isomorphism theorem we obtain
. Then by the second isomorphism theorem we obtain
 $$ \begin{align*} G_1/G_2&=G_1/(G_1\cap \mathcal{N}(N_0,\dots,N_k))\\ &\simeq G_1(N_0,\dots,N_k)/\mathcal{N}(N_0,\dots,N_k)\leq G/\mathcal{N}(N_0,\dots,N_k). \end{align*} $$
$$ \begin{align*} G_1/G_2&=G_1/(G_1\cap \mathcal{N}(N_0,\dots,N_k))\\ &\simeq G_1(N_0,\dots,N_k)/\mathcal{N}(N_0,\dots,N_k)\leq G/\mathcal{N}(N_0,\dots,N_k). \end{align*} $$
In particular
![]() $G_1/G_2$
is finite. We know that a finite-index subgroup of an oligomorphic group is oligomorphic (see for instance Proposition 6.23 in [Reference Bodirsky and Bodor11]). Therefore
$G_1/G_2$
is finite. We know that a finite-index subgroup of an oligomorphic group is oligomorphic (see for instance Proposition 6.23 in [Reference Bodirsky and Bodor11]). Therefore
![]() $G_2$
is also oligomorphic.
$G_2$
is also oligomorphic.
![]() $G_2$
is also closed since it is an intersection of two closed groups. Thus by Lemma 3.25 it follows that
$G_2$
is also closed since it is an intersection of two closed groups. Thus by Lemma 3.25 it follows that
![]() $\mathcal {N}(N_0,\dots ,N_k)\leq G_2\leq G$
. Since
$\mathcal {N}(N_0,\dots ,N_k)\leq G_2\leq G$
. Since
![]() $|G:\mathcal {N}(N_0,\dots ,N_k)|< \infty $
this implies both statements of the lemma.
$|G:\mathcal {N}(N_0,\dots ,N_k)|< \infty $
this implies both statements of the lemma.
Lemma 3.35. Every group in
![]() $\mathcal {H}'$
is closed.
$\mathcal {H}'$
is closed.
Proof We show by induction on n that every group in
![]() $\mathcal {H}_n'$
is closed. For
$\mathcal {H}_n'$
is closed. For
![]() $n=-1$
there is nothing to prove. For the induction step let us assume that
$n=-1$
there is nothing to prove. For the induction step let us assume that
![]() $G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some
$G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some
![]() $H,N_0,\dots ,N_k,N=\prod _{i=0}^kN_i\in \mathcal {H}_{n-1}'$
. By item (i) of Lemma 2.4 we know that the groups
$H,N_0,\dots ,N_k,N=\prod _{i=0}^kN_i\in \mathcal {H}_{n-1}'$
. By item (i) of Lemma 2.4 we know that the groups
![]() $N_i\wr \operatorname {Sym}(\omega )\colon 1\leq i \leq k$
are closed. Thus the direct product
$N_i\wr \operatorname {Sym}(\omega )\colon 1\leq i \leq k$
are closed. Thus the direct product
![]() $\mathcal {N}(N_0,\dots ,N_k)=\operatorname {id}(Y_0\times \{0\})\times \prod _{i=1}^k(N_i\wr \operatorname {Sym}(\omega ))$
is also closed (see Section 2.4). Since the group
$\mathcal {N}(N_0,\dots ,N_k)=\operatorname {id}(Y_0\times \{0\})\times \prod _{i=1}^k(N_i\wr \operatorname {Sym}(\omega ))$
is also closed (see Section 2.4). Since the group
![]() $\mathcal {N}(N_0,\dots ,N_k)$
is contained in
$\mathcal {N}(N_0,\dots ,N_k)$
is contained in
![]() $\mathcal {H}_n'$
, and it is a normal subgroup of
$\mathcal {H}_n'$
, and it is a normal subgroup of
![]() $\mathcal {G}(H;N_0,\dots ,N_k)$
it follows from Lemma 3.34 that
$\mathcal {G}(H;N_0,\dots ,N_k)$
it follows from Lemma 3.34 that
![]() $|G:\mathcal {N}(N_0,\dots ,N_k)|$
is finite. This means that G is a finite union of cosets of
$|G:\mathcal {N}(N_0,\dots ,N_k)|$
is finite. This means that G is a finite union of cosets of
![]() $\mathcal {N}(N_0,\dots ,N_k)$
, and thus a finite union of closed sets. Hence G is closed.
$\mathcal {N}(N_0,\dots ,N_k)$
, and thus a finite union of closed sets. Hence G is closed.
By Lemma 3.35 we can remove the condition “closed” from the formulation of Lemma 3.34.
Corollary 3.36. Let
![]() $G\in \mathcal {H}'$
. Then G has finitely many normal subgroups contained in
$G\in \mathcal {H}'$
. Then G has finitely many normal subgroups contained in
![]() $\mathcal {H}'$
, and all of these have a finite index in G.
$\mathcal {H}'$
, and all of these have a finite index in G.
Lemma 3.37.
![]() $\mathcal {H}_n'\subset \mathcal {H}_n$
for all
$\mathcal {H}_n'\subset \mathcal {H}_n$
for all
![]() $n\in \omega $
(see Definition 3.4).
$n\in \omega $
(see Definition 3.4).
Proof We prove the lemma by induction on n. For
![]() $n=-1$
the statement is trivial. For the induction step let us assume that
$n=-1$
the statement is trivial. For the induction step let us assume that
![]() $G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some
$G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some
![]() $H,N_0,\dots ,N_k,N=\prod _{i=0}^kN_i\in \mathcal {H}_{n-1}'$
. By Corollary 3.18 and Lemma 3.19 it follows that
$H,N_0,\dots ,N_k,N=\prod _{i=0}^kN_i\in \mathcal {H}_{n-1}'$
. By Corollary 3.18 and Lemma 3.19 it follows that
![]() $\prod _{i=1}^k(N_i\wr \operatorname {Sym}(\omega ))\times N_0=\mathcal {N}(N_0,\dots ,N_k)\in \mathcal {H}_n$
. Since
$\prod _{i=1}^k(N_i\wr \operatorname {Sym}(\omega ))\times N_0=\mathcal {N}(N_0,\dots ,N_k)\in \mathcal {H}_n$
. Since
![]() $\mathcal {H}_n$
is closed under taking closed supergroups it follows that
$\mathcal {H}_n$
is closed under taking closed supergroups it follows that
![]() $\overline {G}\in \mathcal {H}_n$
. Finally we have
$\overline {G}\in \mathcal {H}_n$
. Finally we have
![]() $\overline {G}=G$
by Lemma 3.35.
$\overline {G}=G$
by Lemma 3.35.
Now we show that in fact
![]() $\mathcal {H}_n=\mathcal {H}_n'$
for all n. We prove this by induction on n. For the induction step we first show that if
$\mathcal {H}_n=\mathcal {H}_n'$
for all n. We prove this by induction on n. For the induction step we first show that if
![]() $\mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
, and if
$\mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
, and if
![]() $G\in \mathcal {H}$
with
$G\in \mathcal {H}$
with
![]() $\omega $
-partition
$\omega $
-partition
![]() $P=(K, \nabla , \Delta )$
with components
$P=(K, \nabla , \Delta )$
with components
![]() $G_0,\dots ,G_k$
then G has a subgroup S which is isomorphic to a group of the form
$G_0,\dots ,G_k$
then G has a subgroup S which is isomorphic to a group of the form
![]() $\{\operatorname {id}(K)\}\times \prod _{i=1}^m(G_i\wr \operatorname {Sym}(\omega ))$
. First we show this in the case when
$\{\operatorname {id}(K)\}\times \prod _{i=1}^m(G_i\wr \operatorname {Sym}(\omega ))$
. First we show this in the case when
![]() $K=\emptyset $
, and
$K=\emptyset $
, and
![]() $\nabla $
is the universal congruence. The proof of this step is based on the argument presented in Case 2 of the proof of Lemma 3.3, part (i) in [Reference Lachlan34].
$\nabla $
is the universal congruence. The proof of this step is based on the argument presented in Case 2 of the proof of Lemma 3.3, part (i) in [Reference Lachlan34].
Lemma 3.38. Let us assume that
![]() $\mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
.
$\mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
.
Let
![]() $G\in \mathcal {H}_n$
be a permutation group with
$G\in \mathcal {H}_n$
be a permutation group with
![]() $\operatorname {Dom}(G)=X$
, and let
$\operatorname {Dom}(G)=X$
, and let
![]() $P=(\emptyset , X^2, \Delta )$
be the
$P=(\emptyset , X^2, \Delta )$
be the
![]() $\omega $
-partition of G. Let
$\omega $
-partition of G. Let
![]() $Y_0\in X/\Delta $
. Then there exists a map
$Y_0\in X/\Delta $
. Then there exists a map
![]() $p\colon X\rightarrow Y_0$
such that:
$p\colon X\rightarrow Y_0$
such that:
-
(1)
 $p|_{Y_0}=\operatorname {id}(Y_0)$
,
$p|_{Y_0}=\operatorname {id}(Y_0)$
, -
(2) p defines a bijection from Y to
 $Y_0$
for all
$Y_0$
for all
 $Y\in X/\Delta $
, and
$Y\in X/\Delta $
, and -
(3) for all
 $\sigma \in \operatorname {Sym}(\omega )$
there exists a permutation
$\sigma \in \operatorname {Sym}(\omega )$
there exists a permutation
 $\hat {\sigma }\in G$
which acts on
$\hat {\sigma }\in G$
which acts on
 $X/\Delta $
as
$X/\Delta $
as
 $\sigma $
, and such that
$\sigma $
, and such that
 $p(\hat {\sigma }(u))=p(u)$
for all
$p(\hat {\sigma }(u))=p(u)$
for all
 $u\in X$
.
$u\in X$
.
Proof Let
![]() $Y_0,Y_1,\dots $
be an enumeration of all
$Y_0,Y_1,\dots $
be an enumeration of all
![]() $\Delta $
-classes of X. For a subset S of
$\Delta $
-classes of X. For a subset S of
![]() $\omega $
we define
$\omega $
we define
![]() $Y_S:=\bigcup _{j\in S}(Y_j)$
. Let
$Y_S:=\bigcup _{j\in S}(Y_j)$
. Let
We use the notation
![]() $N_j,H_j$
for the groups
$N_j,H_j$
for the groups
![]() $N_{\{j\}}=G_{((Y_j))}$
and
$N_{\{j\}}=G_{((Y_j))}$
and
![]() $H_{\{j\}}=G_{(Y_j)}$
, respectively. It follows from the definition that for all
$H_{\{j\}}=G_{(Y_j)}$
, respectively. It follows from the definition that for all
![]() $S\subset \omega $
the group
$S\subset \omega $
the group
![]() $N_S$
is closed, and
$N_S$
is closed, and
![]() $N_S$
is a normal subgroup of
$N_S$
is a normal subgroup of
![]() $H_S$
. Also we have
$H_S$
. Also we have
![]() $\prod _{j\in S}N_j\subset N_S$
. By definition every
$\prod _{j\in S}N_j\subset N_S$
. By definition every
![]() $N_j$
is a component of the
$N_j$
is a component of the
![]() $\omega $
-partition P. Therefore
$\omega $
-partition P. Therefore
![]() $N_j\in \mathcal {H}_{n-1}$
for all
$N_j\in \mathcal {H}_{n-1}$
for all
![]() $j\in \omega $
. Then Lemma 3.19 implies that if S is finite then
$j\in \omega $
. Then Lemma 3.19 implies that if S is finite then
![]() $\prod _{j\in S}N_j\in \mathcal {H}_{n-1}$
. This also implies that the groups
$\prod _{j\in S}N_j\in \mathcal {H}_{n-1}$
. This also implies that the groups
![]() $N_S$
and
$N_S$
and
![]() $\overline {H_S}$
are contained in
$\overline {H_S}$
are contained in
![]() $\mathcal {H}_{n-1}$
since
$\mathcal {H}_{n-1}$
since
![]() $\mathcal {H}_{n-1}$
is closed under taking closed supergroups. Since
$\mathcal {H}_{n-1}$
is closed under taking closed supergroups. Since
![]() $N_S$
is closed, and
$N_S$
is closed, and
![]() $N_S\triangleleft H_S$
it follows that
$N_S\triangleleft H_S$
it follows that
![]() $h^{-1}N_Sh\in N_S$
for all
$h^{-1}N_Sh\in N_S$
for all
![]() $h\in \overline {H_S}$
. Therefore
$h\in \overline {H_S}$
. Therefore
![]() $N_S$
is also a normal subgroup of
$N_S$
is also a normal subgroup of
![]() $\overline {H_S}$
. Since
$\overline {H_S}$
. Since
![]() $\mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
this implies that
$\mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
this implies that
![]() $|\overline {H_S}:N_S|$
is finite by Corollary 3.36. Therefore
$|\overline {H_S}:N_S|$
is finite by Corollary 3.36. Therefore
![]() $|H_S:N_S|$
is also finite (and thus in fact
$|H_S:N_S|$
is also finite (and thus in fact
![]() $H_S$
is closed). This also implies that the group
$H_S$
is closed). This also implies that the group
![]() $G_{X\setminus Y_S} \cap \bigcap _{j\in S}G_{\{Y_j\}}$
is a finite-index normal subgroup of
$G_{X\setminus Y_S} \cap \bigcap _{j\in S}G_{\{Y_j\}}$
is a finite-index normal subgroup of
![]() $\bigcap _{j\in S}G_{\{Y_j\}}$
. The group G acts on
$\bigcap _{j\in S}G_{\{Y_j\}}$
. The group G acts on
![]() $X/\Delta $
as the full symmetric group for all i. This means that
$X/\Delta $
as the full symmetric group for all i. This means that
![]() $\bigcap _{j\in S}G_{\{Y_j\}}$
acts on
$\bigcap _{j\in S}G_{\{Y_j\}}$
acts on
![]() $(X\setminus Y_S)/\Delta $
as the full symmetric group. Since
$(X\setminus Y_S)/\Delta $
as the full symmetric group. Since
![]() $\operatorname {Sym}(\omega )$
has nontrivial finite index subgroup it follows that the group
$\operatorname {Sym}(\omega )$
has nontrivial finite index subgroup it follows that the group
![]() $G_{X\setminus Y_S} \cap \bigcap _{j\in S}G_{\{Y_j\}}$
acts on
$G_{X\setminus Y_S} \cap \bigcap _{j\in S}G_{\{Y_j\}}$
acts on
![]() $(X\setminus Y_S)/\Delta $
as the full symmetric group as well. In particular for any
$(X\setminus Y_S)/\Delta $
as the full symmetric group as well. In particular for any
![]() $j_1,j_2\in \omega \setminus S$
there exists a permutation
$j_1,j_2\in \omega \setminus S$
there exists a permutation
![]() $\mu \in G$
such that:
$\mu \in G$
such that:
-
•
 $\mu $
fixes every
$\mu $
fixes every
 $Y_j$
with
$Y_j$
with
 $j\neq j_1,j_2$
setwise,
$j\neq j_1,j_2$
setwise, -
•
 $\mu $
switches
$\mu $
switches
 $Y_{j_1}$
and
$Y_{j_1}$
and
 $Y_{j_2}$
, and
$Y_{j_2}$
, and -
•
 $\mu |_{Y_S}\in N_S$
.
$\mu |_{Y_S}\in N_S$
.
Let ![]() . Then
. Then
![]() $K_0=H_0\supset K_1\supset \cdots $
, and since G is closed it follows that
$K_0=H_0\supset K_1\supset \cdots $
, and since G is closed it follows that
![]() $\bigcap _{l=0}^\infty {K_l}=N_0$
. Since
$\bigcap _{l=0}^\infty {K_l}=N_0$
. Since
![]() $|H_0:N_0|< \infty $
it follows that there exists an index l such that
$|H_0:N_0|< \infty $
it follows that there exists an index l such that
![]() $K_l=N_0$
, and hence
$K_l=N_0$
, and hence
![]() $K_{l'}=N_0$
for all
$K_{l'}=N_0$
for all
![]() $l'\geq l$
. For all subsets
$l'\geq l$
. For all subsets
![]() $S\subset \omega \setminus \{0\}$
with
$S\subset \omega \setminus \{0\}$
with
![]() $|S|\geq l$
there exists a permutation
$|S|\geq l$
there exists a permutation
![]() $\nu $
in G which fixes
$\nu $
in G which fixes
![]() $Y_0$
, and which maps
$Y_0$
, and which maps
![]() $Y_{\{1,\dots ,|S|\}}$
into
$Y_{\{1,\dots ,|S|\}}$
into
![]() $Y_S$
. Then
$Y_S$
. Then
![]() $\iota (\nu )$
maps
$\iota (\nu )$
maps
![]() $G_{\{Y_0\}}\cap G_{Y_{\{1,\dots ,|S|\}}}$
to
$G_{\{Y_0\}}\cap G_{Y_{\{1,\dots ,|S|\}}}$
to
![]() $G_{\{Y_0\}}\cap G_{Y_S}$
, and thus it maps
$G_{\{Y_0\}}\cap G_{Y_S}$
, and thus it maps
![]() $N_0=K_l$
to
$N_0=K_l$
to
![]() $K_S:=(G_{\{Y_0\}}\cap G_{Y_S})|_{Y_0}$
. On the other hand
$K_S:=(G_{\{Y_0\}}\cap G_{Y_S})|_{Y_0}$
. On the other hand
![]() $\iota (\nu )$
fixes
$\iota (\nu )$
fixes
![]() $N_0=G|_{((Y_0))}$
since
$N_0=G|_{((Y_0))}$
since
![]() $\nu $
fixes
$\nu $
fixes
![]() $Y_0$
. Therefore
$Y_0$
. Therefore
![]() $K_S=N_S$
for all
$K_S=N_S$
for all
![]() $S \subset \omega \setminus \{0\}$
with
$S \subset \omega \setminus \{0\}$
with
![]() $|S|\geq l$
.
$|S|\geq l$
.
![]() $(*)$
$(*)$
Let
![]() $j\in \omega \setminus \{0\}$
. We claim that for every finite set
$j\in \omega \setminus \{0\}$
. We claim that for every finite set
![]() $S\subset \omega \setminus \{0,j\}$
there exists a permutation
$S\subset \omega \setminus \{0,j\}$
there exists a permutation
![]() $\sigma _S$
of G such that:
$\sigma _S$
of G such that:
-
•
 $\sigma _S$
fixes
$\sigma _S$
fixes
 $Y_S$
pointwise,
$Y_S$
pointwise, -
•
 $\sigma _S$
switches
$\sigma _S$
switches
 $Y_0$
and
$Y_0$
and
 $Y_j$
, and
$Y_j$
, and -
•
 $\sigma _S^2|_{Y_0\cup Y_j}=\operatorname {id}(Y_0\cup Y_j)$
.
$\sigma _S^2|_{Y_0\cup Y_j}=\operatorname {id}(Y_0\cup Y_j)$
.
We can assume without loss of generality that
![]() $|S|\geq l$
. Then we have seen that there exists a permutation
$|S|\geq l$
. Then we have seen that there exists a permutation
![]() $\mu _S\in G_{S}$
that switches
$\mu _S\in G_{S}$
that switches
![]() $Y_0$
and
$Y_0$
and
![]() $Y_j$
. By
$Y_j$
. By
![]() $(*)$
it follows that
$(*)$
it follows that
![]() $(\mu _S)^2|_{Y_0}\in N_0$
. This means that there exists a
$(\mu _S)^2|_{Y_0}\in N_0$
. This means that there exists a
![]() $\tau \in G|_{X\setminus Y_0}$
such that
$\tau \in G|_{X\setminus Y_0}$
such that
![]() $\tau |_{Y_0}=\sigma ^2|_{Y_0}$
. Let
$\tau |_{Y_0}=\sigma ^2|_{Y_0}$
. Let
![]() $\sigma _S:=\tau ^{-1}\mu _S$
. Then
$\sigma _S:=\tau ^{-1}\mu _S$
. Then
![]() $\sigma _S$
also switches
$\sigma _S$
also switches
![]() $Y_0$
and
$Y_0$
and
![]() $Y_j$
, and it also fixes
$Y_j$
, and it also fixes
![]() $Y_S$
pointwise. Moreover, we have
$Y_S$
pointwise. Moreover, we have
 $$ \begin{align*} (\sigma_S^2)|_{Y_0}&=(\tau^{-1}\mu_S)^2|_{Y_0}=(\tau^{-1}\mu_S\tau^{-1}|_{\mu_S(Y_0)}\mu_S)|_{Y_0}\\&=(\tau^{-1}\mu_S^2)|_{Y_0}=\tau|_{Y_0}^{-1}(\mu_S)^2|_{Y_0}=\operatorname{id}(Y_0). \end{align*} $$
$$ \begin{align*} (\sigma_S^2)|_{Y_0}&=(\tau^{-1}\mu_S)^2|_{Y_0}=(\tau^{-1}\mu_S\tau^{-1}|_{\mu_S(Y_0)}\mu_S)|_{Y_0}\\&=(\tau^{-1}\mu_S^2)|_{Y_0}=\tau|_{Y_0}^{-1}(\mu_S)^2|_{Y_0}=\operatorname{id}(Y_0). \end{align*} $$
It follows similarly that
![]() $(\sigma _S^2)|_{Y_j}=\operatorname {id}(Y_j)$
. This means that
$(\sigma _S^2)|_{Y_j}=\operatorname {id}(Y_j)$
. This means that
![]() $(\sigma _S^2)|_{Y_0\cup Y_j}=\operatorname {id}(Y_0\cup Y_j)$
.
$(\sigma _S^2)|_{Y_0\cup Y_j}=\operatorname {id}(Y_0\cup Y_j)$
.
Now let
![]() $S_0$
be such any finite subset with
$S_0$
be such any finite subset with
![]() $|S_0|\geq l$
. We claim that for every finite subset S of
$|S_0|\geq l$
. We claim that for every finite subset S of
![]() $\omega \setminus \{0,j\}$
there exists a map
$\omega \setminus \{0,j\}$
there exists a map
![]() $\sigma ^{\prime }_S\in G|_{Y^{S'}}$
such that
$\sigma ^{\prime }_S\in G|_{Y^{S'}}$
such that
![]() $\sigma _S'|_{Y_0\cup Y_j}=\sigma _{S_0}|_{Y_0\cup Y_j}$
. (
$\sigma _S'|_{Y_0\cup Y_j}=\sigma _{S_0}|_{Y_0\cup Y_j}$
. (![]() ) This is enough to show in the case when
) This is enough to show in the case when
![]() $S'\supset S_0$
. In this case
$S'\supset S_0$
. In this case
![]() $\sigma _{S_0}\sigma _S^{-1}$
fixes
$\sigma _{S_0}\sigma _S^{-1}$
fixes
![]() $Y_0$
setwise, and
$Y_0$
setwise, and
![]() $Y_{S_0}$
pointwise. Therefore by
$Y_{S_0}$
pointwise. Therefore by
![]() $(*)$
we know that there exists a
$(*)$
we know that there exists a
![]() $\tau '\in G|_{X\setminus Y_0}$
such that
$\tau '\in G|_{X\setminus Y_0}$
such that
![]() $\tau '|_{Y_0}=(\sigma _{S_0}\sigma _S^{-1})|_{Y_0}$
. By symmetrical argument we can also find a
$\tau '|_{Y_0}=(\sigma _{S_0}\sigma _S^{-1})|_{Y_0}$
. By symmetrical argument we can also find a
![]() $\tau "\in G|_{X\setminus Y^j}$
such that
$\tau "\in G|_{X\setminus Y^j}$
such that
![]() $\tau "|_{Y_j}=(\sigma _{S_0}\sigma _S^{-1})|_{Y_j}$
. Let
$\tau "|_{Y_j}=(\sigma _{S_0}\sigma _S^{-1})|_{Y_j}$
. Let ![]() . Then
. Then
![]() $\tau |_{Y_0\cup Y_j}=(\sigma _{S_0}\sigma _S^{-1})|_{Y_0\cup Y_j}$
. Let
$\tau |_{Y_0\cup Y_j}=(\sigma _{S_0}\sigma _S^{-1})|_{Y_0\cup Y_j}$
. Let ![]() . Then
. Then
![]() $\sigma _S'$
switches
$\sigma _S'$
switches
![]() $Y_0$
and
$Y_0$
and
![]() $Y_1$
, fixes S pointwise, and
$Y_1$
, fixes S pointwise, and
Since G is closed it also follows from ![]() that there exists a
that there exists a
![]() $\sigma \in G$
such that
$\sigma \in G$
such that
![]() $\sigma |_{Y_0\cup Y_j}=\sigma _S|_{Y_0\cup Y_j}$
and
$\sigma |_{Y_0\cup Y_j}=\sigma _S|_{Y_0\cup Y_j}$
and
![]() $\sigma $
fixes every element outside
$\sigma $
fixes every element outside
![]() $Y_0\cup Y_j$
. In particular
$Y_0\cup Y_j$
. In particular
![]() $\sigma $
switches the classes
$\sigma $
switches the classes
![]() $Y_0$
and
$Y_0$
and
![]() $Y_j$
, and
$Y_j$
, and
![]() $\sigma ^2|_{Y_0\cup Y_j}=\operatorname {id}(Y_0\cup Y_j)$
, and thus
$\sigma ^2|_{Y_0\cup Y_j}=\operatorname {id}(Y_0\cup Y_j)$
, and thus
![]() $\sigma ^2=\operatorname {id}(X)$
.
$\sigma ^2=\operatorname {id}(X)$
.
We define p on
![]() $Y_j$
as
$Y_j$
as
![]() $\sigma |_{Y_j}$
for the map
$\sigma |_{Y_j}$
for the map
![]() $\sigma $
as above defined for j. We extend p to
$\sigma $
as above defined for j. We extend p to
![]() $Y_0$
as the identity map. Then p satisfies conditions 1 and 2 of the lemma. We show that it also satisfies condition 3.
$Y_0$
as the identity map. Then p satisfies conditions 1 and 2 of the lemma. We show that it also satisfies condition 3.
For a permutation
![]() $\sigma \in \operatorname {Sym}(\omega )$
there exists a unique permutation
$\sigma \in \operatorname {Sym}(\omega )$
there exists a unique permutation
![]() $\hat {\sigma }\in \operatorname {Sym}(X)$
such that
$\hat {\sigma }\in \operatorname {Sym}(X)$
such that
![]() $p(\hat {\sigma }(u))=p(u)$
for all
$p(\hat {\sigma }(u))=p(u)$
for all
![]() $u\in X$
, and
$u\in X$
, and
![]() $\hat {\sigma }/\Delta =\sigma $
. We have to show that
$\hat {\sigma }/\Delta =\sigma $
. We have to show that
![]() $\hat {\sigma }\in G$
for all
$\hat {\sigma }\in G$
for all
![]() $\sigma \in \operatorname {Sym}(\omega )$
. By the definition of p it follows that
$\sigma \in \operatorname {Sym}(\omega )$
. By the definition of p it follows that
![]() $\hat {\sigma }\in G$
for every transposition
$\hat {\sigma }\in G$
for every transposition
![]() $\sigma =(0\,j)\in \operatorname {Sym}(\omega )$
. The map
$\sigma =(0\,j)\in \operatorname {Sym}(\omega )$
. The map
![]() $\sigma \mapsto \hat {\sigma }$
is a continuous group homomorphism. Therefore
$\sigma \mapsto \hat {\sigma }$
is a continuous group homomorphism. Therefore
![]() $\{\sigma \in \operatorname {Sym}(\omega )\colon \hat {\sigma }\in G\}$
is a closed subgroup of
$\{\sigma \in \operatorname {Sym}(\omega )\colon \hat {\sigma }\in G\}$
is a closed subgroup of
![]() $\operatorname {Sym}(\omega )$
. Since the transpositions of the from
$\operatorname {Sym}(\omega )$
. Since the transpositions of the from
![]() $(0\,j)\colon j\in \omega \setminus \{0\}$
generate a dense subgroup of
$(0\,j)\colon j\in \omega \setminus \{0\}$
generate a dense subgroup of
![]() $\operatorname {Sym}(\omega )$
this implies that in fact
$\operatorname {Sym}(\omega )$
this implies that in fact
![]() $\{\sigma \in \operatorname {Sym}(\omega )\colon \hat {\sigma }\in G\}=\operatorname {Sym}(\omega )$
, i.e.,
$\{\sigma \in \operatorname {Sym}(\omega )\colon \hat {\sigma }\in G\}=\operatorname {Sym}(\omega )$
, i.e.,
![]() $\hat {\sigma }\in G$
for all
$\hat {\sigma }\in G$
for all
![]() $\sigma \in \operatorname {Sym}(\omega )$
. This finishes the proof of the lemma.
$\sigma \in \operatorname {Sym}(\omega )$
. This finishes the proof of the lemma.
Corollary 3.39. Assume that
![]() $\mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
.
$\mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
.
Let
![]() $G\in \mathcal {H}_n$
be a permutation group with
$G\in \mathcal {H}_n$
be a permutation group with
![]() $\operatorname {Dom}(G)=X$
, and let
$\operatorname {Dom}(G)=X$
, and let
![]() $P=(\emptyset , X^2, \Delta )$
be the
$P=(\emptyset , X^2, \Delta )$
be the
![]() $\omega $
-partition of G. Let
$\omega $
-partition of G. Let
![]() $Y_0\in X/\Delta $
. Then G contains a group
$Y_0\in X/\Delta $
. Then G contains a group
![]() $G^*$
so that P is also an
$G^*$
so that P is also an
![]() $\omega $
-partition of
$\omega $
-partition of
![]() $G^*$
with the same components, and
$G^*$
with the same components, and
![]() $G^*$
is isomorphic to
$G^*$
is isomorphic to
![]() $G_{((Y_0))}\wr \operatorname {Sym}(\omega )$
.
$G_{((Y_0))}\wr \operatorname {Sym}(\omega )$
.
Proof Let p be as in the statement of Lemma 3.38, and let
![]() $Y_0,Y_1,\dots $
be the
$Y_0,Y_1,\dots $
be the
![]() $\Delta $
-classes in X. We define
$\Delta $
-classes in X. We define
![]() $e\colon X\rightarrow Y_0\times \omega , u\mapsto (p(u),q(u))$
where
$e\colon X\rightarrow Y_0\times \omega , u\mapsto (p(u),q(u))$
where
![]() $q(u)$
denotes the unique j such that
$q(u)$
denotes the unique j such that
![]() $u\in Y_j$
. Then e is a bijection between X and
$u\in Y_j$
. Then e is a bijection between X and
![]() $Y_0\times \omega $
. Let
$Y_0\times \omega $
. Let ![]() . Then since G is closed it is clear that G contains
. Then since G is closed it is clear that G contains
![]() $\prod _{i=0}^\infty N_i$
. The image of this direct product according to
$\prod _{i=0}^\infty N_i$
. The image of this direct product according to
![]() $\iota (e)$
is exactly
$\iota (e)$
is exactly
![]() $N_0^\omega $
. Using the map
$N_0^\omega $
. Using the map
![]() $\sigma \mapsto \hat {\sigma }$
as in the proof of Lemma 3.38 it is easy to see that the map
$\sigma \mapsto \hat {\sigma }$
as in the proof of Lemma 3.38 it is easy to see that the map
![]() $\sigma \mapsto e(\hat {\sigma })$
maps
$\sigma \mapsto e(\hat {\sigma })$
maps
![]() $\operatorname {Sym}(\omega )$
into
$\operatorname {Sym}(\omega )$
into
![]() $\{\operatorname {id}(Y_0)\}\wr \operatorname {Sym}(\omega )$
. Therefore the image of e contains
$\{\operatorname {id}(Y_0)\}\wr \operatorname {Sym}(\omega )$
. Therefore the image of e contains
![]() $Y_0\wr \operatorname {Sym}(\omega )$
. We put
$Y_0\wr \operatorname {Sym}(\omega )$
. We put ![]() . Then
. Then
![]() $G^*$
satisfies the conditions of the lemma.
$G^*$
satisfies the conditions of the lemma.
Lemma 3.40. Assume that
![]() $\mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
.
$\mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
.
Let
![]() $G\in \mathcal {H}_n$
be a permutation group with
$G\in \mathcal {H}_n$
be a permutation group with
![]() $\operatorname {Dom}(G)=X$
, and let
$\operatorname {Dom}(G)=X$
, and let
![]() $P=(K, \nabla , \Delta )$
be the
$P=(K, \nabla , \Delta )$
be the
![]() $\omega $
-partition of G. Let
$\omega $
-partition of G. Let
![]() $X_1,\dots ,X_k$
denote the
$X_1,\dots ,X_k$
denote the
![]() $\nabla $
-classes. Let
$\nabla $
-classes. Let
![]() $Y_i\in X_i/\Delta $
for all
$Y_i\in X_i/\Delta $
for all
![]() $i=1,\dots ,k$
. Let
$i=1,\dots ,k$
. Let ![]() . Then G contains a group
. Then G contains a group
![]() $G^*$
so that P is also an
$G^*$
so that P is also an
![]() $\omega $
-partition of
$\omega $
-partition of
![]() $G^*$
with the same components as G, and
$G^*$
with the same components as G, and
![]() $G^*$
is isomorphic to
$G^*$
is isomorphic to
![]() $\mathcal {N}(\{\operatorname {id}(Y_0)\},N_1,\dots ,N_k)$
.
$\mathcal {N}(\{\operatorname {id}(Y_0)\},N_1,\dots ,N_k)$
.
Proof Let ![]() . Then the groups
. Then the groups
![]() $G_i$
are closed, and
$G_i$
are closed, and ![]() is an
is an
![]() $\omega $
-partition of
$\omega $
-partition of
![]() $G_i$
with every component isomorphic to
$G_i$
with every component isomorphic to
![]() $N_i$
. By Corollary 3.39 it follows that
$N_i$
. By Corollary 3.39 it follows that
![]() $G_i$
contains a group
$G_i$
contains a group
![]() $G_i^*$
such that
$G_i^*$
such that
![]() $P_i$
is also an
$P_i$
is also an
![]() $\omega $
-partition of
$\omega $
-partition of
![]() $G_i^*$
and
$G_i^*$
and
![]() $G_i^*$
is isomorphic to
$G_i^*$
is isomorphic to
![]() $N_i\wr \operatorname {Sym}(\omega )$
. By renaming the elements of X we can assume that
$N_i\wr \operatorname {Sym}(\omega )$
. By renaming the elements of X we can assume that
![]() $G_i^*=N_i\wr \operatorname {Sym}(\omega )$
and
$G_i^*=N_i\wr \operatorname {Sym}(\omega )$
and
![]() $K=Y_0\times \{0\}$
for some set
$K=Y_0\times \{0\}$
for some set
![]() $Y_0$
which is disjoint from
$Y_0$
which is disjoint from
![]() $\bigcup _{i=1}^kY_i$
. Then
$\bigcup _{i=1}^kY_i$
. Then ![]() is a subgroup of G, and P is an
is a subgroup of G, and P is an
![]() $\omega $
-partition of
$\omega $
-partition of
![]() $G^*$
with the same component as G. This finishes the proof of the lemma.
$G^*$
with the same component as G. This finishes the proof of the lemma.
Theorem 3.41.
![]() $\mathcal {H}_n=\mathcal {H}_n'$
.
$\mathcal {H}_n=\mathcal {H}_n'$
.
Proof Lemma 3.37 shows the inclusion
![]() $\mathcal {H}_n'\subset \mathcal {H}_n$
.
$\mathcal {H}_n'\subset \mathcal {H}_n$
.
Now we show
![]() $\mathcal {H}_n\subset \mathcal {H}_n'$
by induction on n. For
$\mathcal {H}_n\subset \mathcal {H}_n'$
by induction on n. For
![]() $n=-1$
there is nothing to prove. For the induction step let us assume that
$n=-1$
there is nothing to prove. For the induction step let us assume that
![]() $\mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
, and let
$\mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
, and let
![]() $G\in \mathcal {H}$
with an
$G\in \mathcal {H}$
with an
![]() $\omega $
-partition
$\omega $
-partition
![]() $P=(K, \nabla , \Delta )$
. Let
$P=(K, \nabla , \Delta )$
. Let
![]() $G^*$
be a subgroup as in Lemma 3.39. We can assume without loss of generality that
$G^*$
be a subgroup as in Lemma 3.39. We can assume without loss of generality that
![]() $G^*=\mathcal {N}(\{\operatorname {id}(Y_0)\},N_1,\dots ,N_k)$
where
$G^*=\mathcal {N}(\{\operatorname {id}(Y_0)\},N_1,\dots ,N_k)$
where
![]() $N_i\in \mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
. It follows from the construction of
$N_i\in \mathcal {H}_{n-1}=\mathcal {H}_{n-1}'$
. It follows from the construction of
![]() $G^*$
that
$G^*$
that
where
![]() $Y_i=\operatorname {Dom}(N_i)$
. Let us observe that the equivalence relations
$Y_i=\operatorname {Dom}(N_i)$
. Let us observe that the equivalence relations
![]() $\nabla $
and
$\nabla $
and
![]() $\Delta $
as defined in Definition 3.21 coincide with the relations
$\Delta $
as defined in Definition 3.21 coincide with the relations
![]() $\nabla $
and
$\nabla $
and
![]() $\Delta $
coming from the partition P. In particular G preserves these equivalence relations, and also preserves the set
$\Delta $
coming from the partition P. In particular G preserves these equivalence relations, and also preserves the set
![]() $K:=Y_0\times \{0\}$
. Therefore we can apply Lemma 3.30 to the groups
$K:=Y_0\times \{0\}$
. Therefore we can apply Lemma 3.30 to the groups
![]() $G^*=\mathcal {N}(\{\operatorname {id}(Y_0)\},N_1,\dots ,N_k)$
and G. We obtain that
$G^*=\mathcal {N}(\{\operatorname {id}(Y_0)\},N_1,\dots ,N_k)$
and G. We obtain that
![]() $G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some group H with
$G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some group H with ![]() . Therefore in order to prove that
. Therefore in order to prove that
![]() $G\in \mathcal {H}_n'$
it remains to show that
$G\in \mathcal {H}_n'$
it remains to show that
![]() $N,H\in \mathcal {H}_{n-1}'=\mathcal {H}_{n-1}$
. By Lemma 3.19 we know that
$N,H\in \mathcal {H}_{n-1}'=\mathcal {H}_{n-1}$
. By Lemma 3.19 we know that
![]() $N=\prod _{i=1}^kN_i\in \mathcal {H}_{n-1}$
. Since
$N=\prod _{i=1}^kN_i\in \mathcal {H}_{n-1}$
. Since
![]() $\mathcal {H}_{n-1}$
is closed under taking closed supergroups it follows that
$\mathcal {H}_{n-1}$
is closed under taking closed supergroups it follows that
![]() $\overline {H}\in \mathcal {H}_{n-1}$
. The same argument as before shows that N is also a normal subgroup of
$\overline {H}\in \mathcal {H}_{n-1}$
. The same argument as before shows that N is also a normal subgroup of
![]() $\overline {H}$
. Then by Corollary 3.36 it follows that
$\overline {H}$
. Then by Corollary 3.36 it follows that
![]() $|\overline {H}:N|<\infty $
. Hence
$|\overline {H}:N|<\infty $
. Hence
![]() $|H:N|$
is also finite, and thus in fact H is closed, and thus
$|H:N|$
is also finite, and thus in fact H is closed, and thus
![]() $H=\overline {H}\in \mathcal {H}_{n-1}$
.
$H=\overline {H}\in \mathcal {H}_{n-1}$
.
We give yet another description of the class
![]() $\mathcal {H}_n$
which we will need later in Section 4.
$\mathcal {H}_n$
which we will need later in Section 4.
Theorem 3.42. Let
![]() $n\in \omega $
. Then a permutation group G is contained in
$n\in \omega $
. Then a permutation group G is contained in
![]() $\mathcal {H}_n$
if and only if there exists a sequence of groups
$\mathcal {H}_n$
if and only if there exists a sequence of groups
![]() $G_0,G_1,\dots ,G_m=G$
such that:
$G_0,G_1,\dots ,G_m=G$
such that:
-
(1)
 $G_0=\{\operatorname {id}(\{\emptyset \})\}$
.
$G_0=\{\operatorname {id}(\{\emptyset \})\}$
. -
(2) For all
 $0\leq i\leq m$
one of the following holds:
$0\leq i\leq m$
one of the following holds:-
(a)
 $G_i\simeq G_j$
for some
$G_i\simeq G_j$
for some
 $j<i$
.
$j<i$
. -
(b)
 $G_i$
is a direct product of some groups
$G_i$
is a direct product of some groups
 $G_j,\ j<i$
.
$G_j,\ j<i$
. -
(c)
 $G_i=G_j\wr \operatorname {Sym}(\omega )$
for some
$G_i=G_j\wr \operatorname {Sym}(\omega )$
for some
 $j<i$
.
$j<i$
. -
(d)
 $G_i$
is a finite-index supergroup of some
$G_i$
is a finite-index supergroup of some
 $G_j,\ j<i$
.
$G_j,\ j<i$
.
-
-
(3) For every sequence of indices
 $i_0<\cdots <i_d$
for which
$i_0<\cdots <i_d$
for which
 $G_{i_l}=G_{i_{l-1}}\wr \operatorname {Sym}(\omega )$
holds we have
$G_{i_l}=G_{i_{l-1}}\wr \operatorname {Sym}(\omega )$
holds we have
 $d\leq n$
.
$d\leq n$
.
Theorem 3.42 has the following straightforward consequence.
Corollary 3.43. A permutation group G is contained in
![]() $\mathcal {H}$
if and only if there exists a sequence of groups
$\mathcal {H}$
if and only if there exists a sequence of groups
![]() $G_0,G_1,\dots ,G_m=G$
which satisfy conditions
$G_0,G_1,\dots ,G_m=G$
which satisfy conditions
![]() $(1)$
and
$(1)$
and
![]() $(2)$
in Theorem 3.42.
$(2)$
in Theorem 3.42.
Corollary 3.43 means in other words that
![]() $\mathcal {H}$
is the smallest class of permutation groups which contains
$\mathcal {H}$
is the smallest class of permutation groups which contains
![]() $G_0=\{\operatorname {id}(\{\emptyset \})\}$
and is closed under isomorphisms, finite direct products, wreath products with
$G_0=\{\operatorname {id}(\{\emptyset \})\}$
and is closed under isomorphisms, finite direct products, wreath products with
![]() $\operatorname {Sym}(\omega )$
, and finite-index supergroups.
$\operatorname {Sym}(\omega )$
, and finite-index supergroups.
Using Theorems 2.13 and 3.6, the statement of Corollary 3.43 can also be written in terms of structures as follows.
Theorem 3.44.
![]() $\mathcal {M}$
is the smallest class of structures which contains a one-element structure, is closed under isomorphisms, and is closed under taking finite disjoint unions, infinitely many copies, and finite-index reducts.
$\mathcal {M}$
is the smallest class of structures which contains a one-element structure, is closed under isomorphisms, and is closed under taking finite disjoint unions, infinitely many copies, and finite-index reducts.
Proof of Theorem 3.42
First we show the “if” direction by induction on m. For
![]() $m=0$
we have
$m=0$
we have
![]() $G_0=\{\operatorname {id}(\{\emptyset \})\}\in \mathcal {H}_0$
so in this case we are done. Let us assume now that
$G_0=\{\operatorname {id}(\{\emptyset \})\}\in \mathcal {H}_0$
so in this case we are done. Let us assume now that
![]() $G_0,G_1,\dots ,G_m$
satisfy the conditions (1)–(3).
$G_0,G_1,\dots ,G_m$
satisfy the conditions (1)–(3).
Case A.
![]() $G_m\simeq G_j$
for some
$G_m\simeq G_j$
for some
![]() $j<m$
. By the induction hypothesis
$j<m$
. By the induction hypothesis
![]() $G_j\in \mathcal {H}_n$
. Then we also have
$G_j\in \mathcal {H}_n$
. Then we also have
![]() $G_m\in \mathcal {H}_n$
since
$G_m\in \mathcal {H}_n$
since
![]() $\mathcal {H}_n$
is closed under isomorphisms.
$\mathcal {H}_n$
is closed under isomorphisms.
Case B.
![]() $G_m$
is a finite direct product of some groups
$G_m$
is a finite direct product of some groups
![]() $G_j,\ j<m$
. In this case it follows from the induction hypothesis that
$G_j,\ j<m$
. In this case it follows from the induction hypothesis that
![]() $G_j\in \mathcal {H}_n$
. Then Lemma 3.19 implies that
$G_j\in \mathcal {H}_n$
. Then Lemma 3.19 implies that
![]() $G_m\in \mathcal {H}_n$
.
$G_m\in \mathcal {H}_n$
.
Case C.
![]() $G_m=G_j\wr \operatorname {Sym}(\omega )$
for some
$G_m=G_j\wr \operatorname {Sym}(\omega )$
for some
![]() $j<m$
. In this case we can apply the induction hypothesis for
$j<m$
. In this case we can apply the induction hypothesis for
![]() $j<m$
and
$j<m$
and
![]() $n-1$
. We obtain that
$n-1$
. We obtain that
![]() $G_j\in \mathcal {H}_{n-1}$
. Then Corollary 3.18 implies that
$G_j\in \mathcal {H}_{n-1}$
. Then Corollary 3.18 implies that
![]() $G_m\in \mathcal {H}_n$
.
$G_m\in \mathcal {H}_n$
.
Case D.
![]() $G_m$
is a finite-index supergroup of some
$G_m$
is a finite-index supergroup of some
![]() $G_j,\ j<m$
. It follows again by the induction hypothesis that
$G_j,\ j<m$
. It follows again by the induction hypothesis that
![]() $G_j\in \mathcal {H}_n$
. Then
$G_j\in \mathcal {H}_n$
. Then
![]() $G_j$
is closed, and thus so is
$G_j$
is closed, and thus so is
![]() $G_m$
. We know that the class
$G_m$
. We know that the class
![]() $\mathcal {H}_n$
is closed under taking closed supergroups. Therefore
$\mathcal {H}_n$
is closed under taking closed supergroups. Therefore
![]() $G_m\in \mathcal {H}_n$
.
$G_m\in \mathcal {H}_n$
.
Now we show the “only if” direction by induction on n.
If
![]() $n=0$
then G is finite. Then we can assume that
$n=0$
then G is finite. Then we can assume that
![]() $G\leq \operatorname {Sym}(k)$
for some
$G\leq \operatorname {Sym}(k)$
for some
![]() $k\in \omega $
. Then the sequence of groups
$k\in \omega $
. Then the sequence of groups ![]() for
for
![]() $i<k$
,
$i<k$
,
![]() $G_k=\{\operatorname {id}(k)\}=\prod _{i=0}^{k-1}\{\operatorname {id}(\{i\})\}$
,
$G_k=\{\operatorname {id}(k)\}=\prod _{i=0}^{k-1}\{\operatorname {id}(\{i\})\}$
,
![]() $G_{k+1}=G$
satisfy conditions (1)–(3).
$G_{k+1}=G$
satisfy conditions (1)–(3).
For the induction step let us assume that
![]() $G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some
$G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some
![]() $H,N_0,\dots ,N_k,N\in \mathcal {H}_{n-1}$
. Then by the induction hypothesis we know that there is a sequence
$H,N_0,\dots ,N_k,N\in \mathcal {H}_{n-1}$
. Then by the induction hypothesis we know that there is a sequence
![]() $G_0,\dots ,G_m$
which satisfies conditions (1)–(3) for
$G_0,\dots ,G_m$
which satisfies conditions (1)–(3) for
![]() $n-1$
and which contains all groups
$n-1$
and which contains all groups
![]() $H,N_0,\dots ,N_k$
. Then let
$H,N_0,\dots ,N_k$
. Then let

Then clearly the groups
![]() $G_0,\dots ,G_{m+k+1}$
satisfy conditions (1)–(3) with n. The only thing we have to check that we can add
$G_0,\dots ,G_{m+k+1}$
satisfy conditions (1)–(3) with n. The only thing we have to check that we can add
![]() $G=G_{m+k+2}$
to this sequence. For this it is enough to show that
$G=G_{m+k+2}$
to this sequence. For this it is enough to show that
![]() $|G:\mathcal {N}(N_0,\dots ,N_k)|$
is finite. Indeed, by Lemma 3.26 we know that the subgroup
$|G:\mathcal {N}(N_0,\dots ,N_k)|$
is finite. Indeed, by Lemma 3.26 we know that the subgroup
![]() $\mathcal {N}(N_0,\dots ,N_k)$
is normal, and thus by Corollary 3.36 its index is finite in G.
$\mathcal {N}(N_0,\dots ,N_k)$
is normal, and thus by Corollary 3.36 its index is finite in G.
3.2. The rank 1 case
Next we focus our attention on the class
![]() $\mathcal {M}_1$
. Using Corollary 3.9 it follows that
$\mathcal {M}_1$
. Using Corollary 3.9 it follows that
![]() $\mathfrak {A}\in \mathcal {M}_1$
if and only if
$\mathfrak {A}\in \mathcal {M}_1$
if and only if
![]() $\operatorname {Aut}(\mathfrak {A})\in \mathcal {H}_1$
. We call these structures cellular. Using Theorem 3.41 and Remark 3.5 we know that
$\operatorname {Aut}(\mathfrak {A})\in \mathcal {H}_1$
. We call these structures cellular. Using Theorem 3.41 and Remark 3.5 we know that
![]() $G\in \mathcal {H}_1$
if and only if G can be written, up to isomorphism, as
$G\in \mathcal {H}_1$
if and only if G can be written, up to isomorphism, as
![]() $G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some groups
$G=\mathcal {G}(H;N_0,\dots ,N_k)$
for some groups ![]() with finite domains.
with finite domains.
In this section we collect some equivalent characterizations of a structure being cellular. We first show a few characterizations of cellular structures in terms of orbit growth on subsets.
Definition 3.45. We say that a group G is P-oligomorphic if
![]() $o^s_n(\mathfrak {A})<cn^k$
for some
$o^s_n(\mathfrak {A})<cn^k$
for some
![]() $c>0$
and
$c>0$
and
![]() $k\in \omega $
.
$k\in \omega $
.
The class of closed P-oligomorphic groups are completely classified in [Reference Falque28]. The following two lemmas follow from the results of [Reference Braunfeld22, Reference Falque28].
Lemma 3.46. Let G be a permutation groups acting on a countable set. Then the following are equivalent:
-
(1) G is P-oligomorphic.
-
(2)
 $o^s_n(\mathfrak {A})\sim cn^k$
for some
$o^s_n(\mathfrak {A})\sim cn^k$
for some
 $c>0$
and
$c>0$
and
 $k\in \omega $
.
$k\in \omega $
. -
(3) For all
 $c>0$
we have
$c>0$
we have
 $o^s_n(\mathfrak {A})<e^{c\sqrt {n}}$
if n is large enough.
$o^s_n(\mathfrak {A})<e^{c\sqrt {n}}$
if n is large enough.
Lemma 3.47. A structure
![]() $\mathfrak {A}$
is cellular if and only if it is stable and its automorphism group is P-oligomorphic.
$\mathfrak {A}$
is cellular if and only if it is stable and its automorphism group is P-oligomorphic.
We can also characterize cellular structure in terms of orbit growth on injective tuples as follows.
Lemma 3.48. A structure
![]() $\mathfrak {A}$
is cellular if and only if
$\mathfrak {A}$
is cellular if and only if
![]() $o^i_n(\mathfrak {A})<cn^{dn}$
for some constants
$o^i_n(\mathfrak {A})<cn^{dn}$
for some constants
![]() $c,d$
with
$c,d$
with
![]() $d<1$
.
$d<1$
.
The advantage of the characterization above is that here we do not have to assume stability; it is automatically implied by the orbit growth condition.
In order to prove Lemma 3.48 we first describe cellularity of a structure in terms of finite coverings. Then Lemma 3.48 is a direct consequence of the results of [Reference Bodirsky and Bodor11].
Definition 3.49. Let
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {B}$
be structures. A mapping
$\mathfrak {B}$
be structures. A mapping
![]() $\pi \colon \mathfrak {A}\rightarrow \mathfrak {B}$
is called a finite cover if:
$\pi \colon \mathfrak {A}\rightarrow \mathfrak {B}$
is called a finite cover if:
-
(1)
 $\pi $
is surjective,
$\pi $
is surjective, -
(2) for each
 $w\in B$
the set
$w\in B$
the set
 $\pi ^{-1}(w)$
is finite,
$\pi ^{-1}(w)$
is finite, -
(3) the equivalence relation
 $\{(a,b)\colon \pi (a)=\pi (b)\}$
is preserved by
$\{(a,b)\colon \pi (a)=\pi (b)\}$
is preserved by
 $\operatorname {Aut}(\mathfrak {A})$
,
$\operatorname {Aut}(\mathfrak {A})$
, -
(4) the image of
 $\operatorname {Aut}(\mathfrak {A})$
under the induced homomorphism
$\operatorname {Aut}(\mathfrak {A})$
under the induced homomorphism
 $\iota (\pi )\colon \operatorname {Aut}(\mathfrak {A})\rightarrow \operatorname {Sym}(B)$
is equal to
$\iota (\pi )\colon \operatorname {Aut}(\mathfrak {A})\rightarrow \operatorname {Sym}(B)$
is equal to
 $\operatorname {Aut}(\mathfrak {B})$
.
$\operatorname {Aut}(\mathfrak {B})$
.
A structure
![]() $\mathfrak {A}$
is called a finite covering of
$\mathfrak {A}$
is called a finite covering of
![]() $\mathfrak {B}$
if there is a finite cover
$\mathfrak {B}$
if there is a finite cover
![]() $\pi \colon \mathfrak {A}\rightarrow \mathfrak {B}$
.
$\pi \colon \mathfrak {A}\rightarrow \mathfrak {B}$
.
Definition 3.50. A structure is called unary if all of its relations are unary.
Using the notion of finite coverings we know the following.
Theorem 3.51. Let
![]() $\mathfrak {A}$
be a structure. Then the following are equivalent.
$\mathfrak {A}$
be a structure. Then the following are equivalent.
-
(1)
 $\mathfrak {A}$
is a finite covering of a reduct of some unary
$\mathfrak {A}$
is a finite covering of a reduct of some unary
 $\omega $
-categorical structure.
$\omega $
-categorical structure. -
(2)
 $\mathfrak {A}$
is a reduct of a finite covering of some unary
$\mathfrak {A}$
is a reduct of a finite covering of some unary
 $\omega $
-categorical structure.
$\omega $
-categorical structure. -
(3)
 $o^i_n(\mathfrak {A})<cn^{dn}$
for some constants
$o^i_n(\mathfrak {A})<cn^{dn}$
for some constants
 $c,d$
with
$c,d$
with
 $d<1$
.
$d<1$
.
Proof See [Reference Bodirsky and Bodor11, Theorem 8.16, item (8.6)].
Now we show that a structure
![]() $\mathfrak {A}$
satisfies condition 2 of Theorem 3.51 if and only if it is cellular. Together with Theorem 3.51 this implies Lemma 3.48.
$\mathfrak {A}$
satisfies condition 2 of Theorem 3.51 if and only if it is cellular. Together with Theorem 3.51 this implies Lemma 3.48.
Lemma 3.52. A structure
![]() $\mathfrak {A}$
is cellular if and only if it is a reduct of a finite covering of some
$\mathfrak {A}$
is cellular if and only if it is a reduct of a finite covering of some
![]() $\omega $
-categorical unary structure.
$\omega $
-categorical unary structure.
Proof First, let us assume that
![]() $\mathfrak {A}$
is cellular. Then we can assume without loss of generality that the automorphism group of
$\mathfrak {A}$
is cellular. Then we can assume without loss of generality that the automorphism group of
![]() $\mathfrak {A}$
can be written as
$\mathfrak {A}$
can be written as
![]() $\operatorname {Aut}(\mathfrak {A})=\mathcal {G}(H;N_0,\dots ,N_k)$
for some finite domain permutation groups
$\operatorname {Aut}(\mathfrak {A})=\mathcal {G}(H;N_0,\dots ,N_k)$
for some finite domain permutation groups
![]() $N_0,\dots ,N_k$
and
$N_0,\dots ,N_k$
and ![]() . Let
. Let
![]() $\mathfrak {A}'$
be a structure with
$\mathfrak {A}'$
be a structure with
![]() $\operatorname {Aut}(\mathfrak {A}')=\mathcal {N}(N_0,\dots ,N_k)$
. Then it is enough to show that
$\operatorname {Aut}(\mathfrak {A}')=\mathcal {N}(N_0,\dots ,N_k)$
. Then it is enough to show that
![]() $\mathfrak {A}'$
is a finite covering of some unary
$\mathfrak {A}'$
is a finite covering of some unary
![]() $\omega $
-categorical structure. Let
$\omega $
-categorical structure. Let
![]() $\pi $
be the map sending every element to its
$\pi $
be the map sending every element to its
![]() $\Delta $
class. We identify the image of
$\Delta $
class. We identify the image of
![]() $\pi $
with
$\pi $
with
![]() $\{(0,0)\}\cup \{1,\dots ,k\}\times \omega $
as in Section 3.1. Then the image of
$\{(0,0)\}\cup \{1,\dots ,k\}\times \omega $
as in Section 3.1. Then the image of
![]() $\operatorname {Aut}(\mathfrak {A}')$
under the homomorphism
$\operatorname {Aut}(\mathfrak {A}')$
under the homomorphism
![]() $\iota (\pi )\colon \operatorname {Aut}(\mathfrak {A}')\rightarrow \operatorname {Sym}(\{(0,0)\}\cup \{1,\dots ,k\}\times \omega )$
induced by
$\iota (\pi )\colon \operatorname {Aut}(\mathfrak {A}')\rightarrow \operatorname {Sym}(\{(0,0)\}\cup \{1,\dots ,k\}\times \omega )$
induced by
![]() $\pi $
is
$\pi $
is
![]() $\operatorname {id}(\{(0,0)\})\times \operatorname {Sym}(\omega )^{[k]}$
. This is exactly the automorphism group of the unary structure
$\operatorname {id}(\{(0,0)\})\times \operatorname {Sym}(\omega )^{[k]}$
. This is exactly the automorphism group of the unary structure
![]() $\mathfrak {B}$
with domain set
$\mathfrak {B}$
with domain set
![]() $A/\Delta $
and with relations for the subsets
$A/\Delta $
and with relations for the subsets
![]() $\{(0,0)\}$
and
$\{(0,0)\}$
and
![]() $\{i\}\times \omega $
for
$\{i\}\times \omega $
for
![]() $i=1,\dots ,k$
. Clearly
$i=1,\dots ,k$
. Clearly
![]() $\mathfrak {B}$
is
$\mathfrak {B}$
is
![]() $\omega $
-categorical which finishes the proof of the “only if” direction of the lemma.
$\omega $
-categorical which finishes the proof of the “only if” direction of the lemma.
Now let us assume that
![]() $\mathfrak {A}$
is a reduct of a finite covering
$\mathfrak {A}$
is a reduct of a finite covering
![]() $\mathfrak {A}'$
of some unary
$\mathfrak {A}'$
of some unary
![]() $\omega $
-categorical structure
$\omega $
-categorical structure
![]() $\mathfrak {B}$
. We claim that
$\mathfrak {B}$
. We claim that
![]() $\mathfrak {A}$
is cellular. We have seen that the class of cellular structure is closed under taking reducts; therefore, it is enough to show that
$\mathfrak {A}$
is cellular. We have seen that the class of cellular structure is closed under taking reducts; therefore, it is enough to show that
![]() $\mathfrak {A}'$
is cellular. We know that
$\mathfrak {A}'$
is cellular. We know that
![]() $\operatorname {Aut}(\mathfrak {B})$
can be written as
$\operatorname {Aut}(\mathfrak {B})$
can be written as
![]() $\prod _{i=1}^n\operatorname {Sym}(U_i)$
for some finite partition
$\prod _{i=1}^n\operatorname {Sym}(U_i)$
for some finite partition
![]() $U_1,\dots ,U_n$
of B (see for instance Lemma 3.1 in [Reference Bodirsky and Bodor11]). We can assume without loss of generality that
$U_1,\dots ,U_n$
of B (see for instance Lemma 3.1 in [Reference Bodirsky and Bodor11]). We can assume without loss of generality that
![]() $U_1,\dots ,U_k$
are infinite, and
$U_1,\dots ,U_k$
are infinite, and
![]() $U_{k+1},\dots ,U_n$
are finite. Let
$U_{k+1},\dots ,U_n$
are finite. Let
![]() $\pi \colon \mathfrak {A}'\rightarrow \mathfrak {B}$
be a finite covering map. We define:
$\pi \colon \mathfrak {A}'\rightarrow \mathfrak {B}$
be a finite covering map. We define:
-
•
 ,
, -
•
 , and
, and -
•
 .
.
Then it is straightforward to verify that ![]() is an
is an
![]() $\omega $
-partition of
$\omega $
-partition of
![]() $\operatorname {Aut}(\mathfrak {A}')$
all of whose components having finite domains. By definition this means exactly that
$\operatorname {Aut}(\mathfrak {A}')$
all of whose components having finite domains. By definition this means exactly that
![]() $\mathfrak {A}'$
is cellular.
$\mathfrak {A}'$
is cellular.
Finally, we mention that in [Reference Braunfeld and Laskowski23] the authors showed that a structure is cellular if and only if it is
![]() $\omega $
-categorical, and mutually algebraic. We skip the definition of mutual algebraicity here, and refer the reader to the aforementioned paper.
$\omega $
-categorical, and mutually algebraic. We skip the definition of mutual algebraicity here, and refer the reader to the aforementioned paper.
We summarize the results mentioned in this section in the following theorem.
Theorem 3.53. Let
![]() $\mathfrak {A}$
be a countable structure. Then the following are equivalent:
$\mathfrak {A}$
be a countable structure. Then the following are equivalent:
-
(1)
 $\mathfrak {A}$
is cellular.
$\mathfrak {A}$
is cellular. -
(2)
 $\mathfrak {A}$
is a finite covering of a reduct of a unary
$\mathfrak {A}$
is a finite covering of a reduct of a unary
 $\omega $
-categorical structure.
$\omega $
-categorical structure. -
(3)
 $\mathfrak {A}$
is a reduct of a finite covering of a unary
$\mathfrak {A}$
is a reduct of a finite covering of a unary
 $\omega $
-categorical structure.
$\omega $
-categorical structure. -
(4)
 $\operatorname {Aut}(\mathfrak {A})\in \mathcal {H}_1$
.
$\operatorname {Aut}(\mathfrak {A})\in \mathcal {H}_1$
. -
(5)
 $\operatorname {Aut}(\mathfrak {A})\simeq \mathcal {G}(H;N_0,\dots ,N_k)$
for some finite domain permutation groups
$\operatorname {Aut}(\mathfrak {A})\simeq \mathcal {G}(H;N_0,\dots ,N_k)$
for some finite domain permutation groups
 $N_i$
and
$N_i$
and
 $H\supset \prod _{i=0}^kN_i$
.
$H\supset \prod _{i=0}^kN_i$
. -
(6)
 $\mathfrak {A}$
is stable, and
$\mathfrak {A}$
is stable, and
 $o^s_n(\mathfrak {A})<cn^k$
for some
$o^s_n(\mathfrak {A})<cn^k$
for some
 $c>0$
and
$c>0$
and
 $k\in \omega $
.
$k\in \omega $
. -
(7)
 $\mathfrak {A}$
is stable, and
$\mathfrak {A}$
is stable, and
 $o^s_n(\mathfrak {A})\sim cn^k$
for some
$o^s_n(\mathfrak {A})\sim cn^k$
for some
 $c>0$
and
$c>0$
and
 $k\in \omega $
.
$k\in \omega $
. -
(8)
 $\mathfrak {A}$
is stable, and for all
$\mathfrak {A}$
is stable, and for all
 $c>0$
we have
$c>0$
we have
 $o^s_n(\mathfrak {A})<e^{c\sqrt {n}}$
if n is large enough.
$o^s_n(\mathfrak {A})<e^{c\sqrt {n}}$
if n is large enough. -
(9)
 $o^i_n(\mathfrak {A})<cn^{dn}$
for some constants
$o^i_n(\mathfrak {A})<cn^{dn}$
for some constants
 $c,d$
with
$c,d$
with
 $d<1$
.
$d<1$
. -
(10)
 $\mathfrak {A}$
is
$\mathfrak {A}$
is
 $\omega $
-categorical and mutually algebraic.
$\omega $
-categorical and mutually algebraic.
4. Homogeneity and finite boundedness
In [Reference Lachlan34] Lachlan showed that every
![]() $\omega $
-categorical monadically stable structure is finitely homogenizable. On the other hand by Theorem 10.1’ in [Reference Knight and Lachlan32] we know that every stable homogeneous structure is finitely bounded. Combining these two statements we obtain that
$\omega $
-categorical monadically stable structure is finitely homogenizable. On the other hand by Theorem 10.1’ in [Reference Knight and Lachlan32] we know that every stable homogeneous structure is finitely bounded. Combining these two statements we obtain that
![]() $\mathcal {M}\subseteq \mathcal {FBH}$
. In this section we reprove this containment using more elementary methods. Furthermore, our proof uses some more general arguments which are not specific to the class
$\mathcal {M}\subseteq \mathcal {FBH}$
. In this section we reprove this containment using more elementary methods. Furthermore, our proof uses some more general arguments which are not specific to the class
![]() $\mathcal {M}$
(or stable structures), and they might work for other classes of structures as well.
$\mathcal {M}$
(or stable structures), and they might work for other classes of structures as well.
Our key observation is that the class
![]() $\mathcal {FBH}$
is closed under taking finite-index reducts; this will be shown in the following subsection. By Corollary 2.34 we know that
$\mathcal {FBH}$
is closed under taking finite-index reducts; this will be shown in the following subsection. By Corollary 2.34 we know that
![]() $\mathcal {FBH}$
is also closed under taking finite disjoint unions and infinite copies. Then by Theorem 3.44 we can conclude that the class
$\mathcal {FBH}$
is also closed under taking finite disjoint unions and infinite copies. Then by Theorem 3.44 we can conclude that the class
![]() $\mathcal {M}$
is contained in
$\mathcal {M}$
is contained in
![]() $\mathcal {FBH}$
.
$\mathcal {FBH}$
.
4.1. Finite-index reducts of homogeneous structures
Lemma 4.1. Let
![]() $\mathfrak {A}$
be an
$\mathfrak {A}$
be an
![]() $\omega $
-categorical structure, and let
$\omega $
-categorical structure, and let
![]() $\mathfrak {B}$
be a reduct of
$\mathfrak {B}$
be a reduct of
![]() $\mathfrak {A}$
. For
$\mathfrak {A}$
. For
![]() $i\in I$
, let
$i\in I$
, let
![]() $\alpha _i$
be such that
$\alpha _i$
be such that ![]() . Then
. Then
![]() $\vec {u}\approx _{\mathfrak {B}}\vec {v}$
iff
$\vec {u}\approx _{\mathfrak {B}}\vec {v}$
iff
![]() $\vec {u}\approx _{\mathfrak {A}}\alpha _i(\vec {v})$
for some
$\vec {u}\approx _{\mathfrak {A}}\alpha _i(\vec {v})$
for some
![]() $i\in I$
.
$i\in I$
.
Proof Since
![]() $\mathfrak {A}$
and thus also
$\mathfrak {A}$
and thus also
![]() $\mathfrak {B}$
are
$\mathfrak {B}$
are
![]() $\omega $
-categorical we have
$\omega $
-categorical we have
 $$ \begin{align*} \vec{u}\approx_{\mathfrak{B}}\vec{v} &\Leftrightarrow \exists (\beta\in \operatorname{Aut}(\mathfrak{B}))(\vec{u}=\beta(\vec{v}))\\ &\Leftrightarrow (\exists i\in I)(\exists \alpha\in \operatorname{Aut}(\mathfrak{A}))(\vec{u}=\alpha\alpha_i(\vec{v})) \Leftrightarrow (\exists i\in I)(\vec{u}\approx_{\mathfrak{A}}\alpha_i(\vec{v})).\\[-34pt] \end{align*} $$
$$ \begin{align*} \vec{u}\approx_{\mathfrak{B}}\vec{v} &\Leftrightarrow \exists (\beta\in \operatorname{Aut}(\mathfrak{B}))(\vec{u}=\beta(\vec{v}))\\ &\Leftrightarrow (\exists i\in I)(\exists \alpha\in \operatorname{Aut}(\mathfrak{A}))(\vec{u}=\alpha\alpha_i(\vec{v})) \Leftrightarrow (\exists i\in I)(\vec{u}\approx_{\mathfrak{A}}\alpha_i(\vec{v})).\\[-34pt] \end{align*} $$
Lemma 4.2. Let
![]() $\mathfrak {A}$
be a homogeneous relational structure with
$\mathfrak {A}$
be a homogeneous relational structure with
![]() $m(\mathfrak {A})=m$
, and let
$m(\mathfrak {A})=m$
, and let
![]() $\mathfrak {B}$
be a reduct of
$\mathfrak {B}$
be a reduct of
![]() $\mathfrak {A}$
with
$\mathfrak {A}$
with
![]() $|\operatorname {Aut}(\mathfrak {B}):\operatorname {Aut}(\mathfrak {A})|=d<\infty $
. Then
$|\operatorname {Aut}(\mathfrak {B}):\operatorname {Aut}(\mathfrak {A})|=d<\infty $
. Then
![]() $\mathfrak {B}$
is interdefinable with a homogeneous structure
$\mathfrak {B}$
is interdefinable with a homogeneous structure
![]() $\mathfrak {B}'$
with
$\mathfrak {B}'$
with
![]() $m(\mathfrak {B}')=dm$
.
$m(\mathfrak {B}')=dm$
.
Proof We check condition (4) of Lemma 2.21 for the structure
![]() $\mathfrak {B}$
and
$\mathfrak {B}$
and
![]() $dm$
. Let
$dm$
. Let
![]() $\vec {u}, \vec {v}\in A^n$
such that
$\vec {u}, \vec {v}\in A^n$
such that
![]() $\vec {u}\not \approx _{\mathfrak {B}}\vec {v}$
. We have to show that
$\vec {u}\not \approx _{\mathfrak {B}}\vec {v}$
. We have to show that
![]() $\vec {u}_{\pi }\not \approx _{\mathfrak {B}} \vec {v}_{\pi }$
for some
$\vec {u}_{\pi }\not \approx _{\mathfrak {B}} \vec {v}_{\pi }$
for some
![]() $\pi \colon dm\rightarrow n$
. Since
$\pi \colon dm\rightarrow n$
. Since
![]() $|\operatorname {Aut}(\mathfrak {B}):\operatorname {Aut}(\mathfrak {A})|=d$
it follows that
$|\operatorname {Aut}(\mathfrak {B}):\operatorname {Aut}(\mathfrak {A})|=d$
it follows that
![]() $\operatorname {Aut}(\mathfrak {B})$
can be written as
$\operatorname {Aut}(\mathfrak {B})$
can be written as
![]() $\operatorname {Aut}(\mathfrak {B})=\bigsqcup _{i<d}(\operatorname {Aut}(\mathfrak {A})\alpha _i)$
for some suitable
$\operatorname {Aut}(\mathfrak {B})=\bigsqcup _{i<d}(\operatorname {Aut}(\mathfrak {A})\alpha _i)$
for some suitable
![]() $\alpha _i,\ i<d$
. Then by Lemma 4.1 we know that
$\alpha _i,\ i<d$
. Then by Lemma 4.1 we know that
![]() $\vec {u}\not \approx _{\mathfrak {A}}\alpha _i(\vec {v})$
for all
$\vec {u}\not \approx _{\mathfrak {A}}\alpha _i(\vec {v})$
for all
![]() $i<d$
. Then by using the implication (1)
$i<d$
. Then by using the implication (1)
![]() $\rightarrow $
(4) of Lemma 2.21 we obtain that for all
$\rightarrow $
(4) of Lemma 2.21 we obtain that for all
![]() $i<d$
there exists some
$i<d$
there exists some
![]() $\pi _i\colon m\rightarrow n$
such that
$\pi _i\colon m\rightarrow n$
such that
![]() $\vec {u}_{\pi _i}\not \approx _{\mathfrak {A}}\alpha _i(\vec {v}_{\pi _i})$
. Let
$\vec {u}_{\pi _i}\not \approx _{\mathfrak {A}}\alpha _i(\vec {v}_{\pi _i})$
. Let
Then
![]() $\vec {u}_{\pi }\not \approx _{\mathfrak {A}}\alpha _i(\vec {v}_{\pi })$
for all
$\vec {u}_{\pi }\not \approx _{\mathfrak {A}}\alpha _i(\vec {v}_{\pi })$
for all
![]() $i< d$
. By using Lemma 4.1 again this implies
$i< d$
. By using Lemma 4.1 again this implies
![]() $\vec {u}_{\pi }\not \approx _{\mathfrak {B}} \vec {v}_{\pi }$
, and this is what we wanted to show.
$\vec {u}_{\pi }\not \approx _{\mathfrak {B}} \vec {v}_{\pi }$
, and this is what we wanted to show.
Lemma 4.2 immediately implies the following.
Corollary 4.3. The class
![]() $\mathcal {FH}$
is closed under taking finite-index reducts.
$\mathcal {FH}$
is closed under taking finite-index reducts.
Proof Let
![]() $\mathfrak {A}\in \mathcal {FH}$
, and let
$\mathfrak {A}\in \mathcal {FH}$
, and let
![]() $\mathfrak {B}$
be a reduct of
$\mathfrak {B}$
be a reduct of
![]() $\mathfrak {A}$
with
$\mathfrak {A}$
with
![]() $|\operatorname {Aut}(\mathfrak {B}):\operatorname {Aut}(\mathfrak {A})|=d<\infty $
. We show that
$|\operatorname {Aut}(\mathfrak {B}):\operatorname {Aut}(\mathfrak {A})|=d<\infty $
. We show that
![]() $\mathfrak {B}\in \mathcal {FH}$
. We can assume without loss of generality that
$\mathfrak {B}\in \mathcal {FH}$
. We can assume without loss of generality that
![]() $\mathfrak {A}$
is homogeneous and has a finite relational signature. Then Lemma 4.2 immediately implies that
$\mathfrak {A}$
is homogeneous and has a finite relational signature. Then Lemma 4.2 immediately implies that
![]() $\mathfrak {B}$
is interdefinable with a homogeneous structure with a finite relational signature.
$\mathfrak {B}$
is interdefinable with a homogeneous structure with a finite relational signature.
Now we show that the class
![]() $\mathcal {FBH}$
is also closed under taking finite-index reducts.
$\mathcal {FBH}$
is also closed under taking finite-index reducts.
Lemma 4.4. Let
![]() $\mathfrak {A}$
be a homogeneous finitely bounded structure with signature
$\mathfrak {A}$
be a homogeneous finitely bounded structure with signature
![]() $\sigma $
, and let
$\sigma $
, and let ![]() . Let
. Let
![]() $\tau \subset \sigma $
, and let
$\tau \subset \sigma $
, and let
![]() $\mathfrak {B}$
be a
$\mathfrak {B}$
be a
![]() $\tau $
-reduct of
$\tau $
-reduct of
![]() $\mathfrak {A}$
which is also homogeneous. Let
$\mathfrak {A}$
which is also homogeneous. Let
![]() $\mathfrak {C}$
be a
$\mathfrak {C}$
be a
![]() $\tau $
-structure, and let
$\tau $
-structure, and let
![]() $a_0,\dots ,a_m$
be pairwise distinct elements in
$a_0,\dots ,a_m$
be pairwise distinct elements in
![]() $\mathfrak {C}$
. Then
$\mathfrak {C}$
. Then
![]() $\mathfrak {C}\in \operatorname {Age}(\mathfrak {B})$
if and only if for all
$\mathfrak {C}\in \operatorname {Age}(\mathfrak {B})$
if and only if for all
![]() $i\leq m$
there exists a
$i\leq m$
there exists a
![]() $\sigma $
-expansion
$\sigma $
-expansion
![]() $\mathfrak {D}_i$
of the structure
$\mathfrak {D}_i$
of the structure
![]() $\mathfrak {C}_i:=\mathfrak {C}|_{C\setminus \{a_i\}}$
such that for all
$\mathfrak {C}_i:=\mathfrak {C}|_{C\setminus \{a_i\}}$
such that for all
![]() $i,j\leq m$
we have:
$i,j\leq m$
we have:
-
(i)
 $\mathfrak {D}_i\in \operatorname {Age}(\mathfrak {A})$
, and
$\mathfrak {D}_i\in \operatorname {Age}(\mathfrak {A})$
, and -
(ii)
 $\mathfrak {D}_i|_{C\setminus \{a_i,a_j\}}=\mathfrak {D}_j|_{C\setminus \{a_i,a_j\}}$
.
$\mathfrak {D}_i|_{C\setminus \{a_i,a_j\}}=\mathfrak {D}_j|_{C\setminus \{a_i,a_j\}}$
.
Proof We use the notation ![]() , and
, and
![]() $C_{ij}=C\setminus \{a_i,a_j\}=C_i\cap C_j$
.
$C_{ij}=C\setminus \{a_i,a_j\}=C_i\cap C_j$
.
Let
![]() $\mathfrak {C}\in \operatorname {Age}(\mathfrak {B})$
. We can assume without loss of generality that
$\mathfrak {C}\in \operatorname {Age}(\mathfrak {B})$
. We can assume without loss of generality that
![]() $\mathfrak {C}$
is a finite substructure of
$\mathfrak {C}$
is a finite substructure of
![]() $\mathfrak {B}$
. Then let
$\mathfrak {B}$
. Then let ![]() , and
, and ![]() . Then obviously
. Then obviously
![]() $\mathfrak {D}_i\in \operatorname {Age}(\mathfrak {A})$
, and
$\mathfrak {D}_i\in \operatorname {Age}(\mathfrak {A})$
, and
![]() $\mathfrak {D}_i|_{C_{ij}}=\mathfrak {D}_j|_{C_{ij}}=\mathfrak {D}|_{C_{ij}}$
.
$\mathfrak {D}_i|_{C_{ij}}=\mathfrak {D}_j|_{C_{ij}}=\mathfrak {D}|_{C_{ij}}$
.
For the other direction we define a
![]() $\sigma $
-structure
$\sigma $
-structure
![]() $\mathfrak {D}$
as follows. The domain set of
$\mathfrak {D}$
as follows. The domain set of
![]() $\mathfrak {D}$
is C, and for all relational symbols
$\mathfrak {D}$
is C, and for all relational symbols
![]() $R\in \sigma $
, a tuple
$R\in \sigma $
, a tuple
![]() $\vec {u}\in C^{\operatorname {ar}(R)}$
is contained in
$\vec {u}\in C^{\operatorname {ar}(R)}$
is contained in
![]() $R^{\mathfrak {D}}$
if and only if there exists some i such that
$R^{\mathfrak {D}}$
if and only if there exists some i such that
![]() $\vec {u}\in R^{\mathfrak {D}_i}$
.
$\vec {u}\in R^{\mathfrak {D}_i}$
.
Claim 1.
![]() $\mathfrak {D}|_{C_i}=\mathfrak {D}_i$
. Let
$\mathfrak {D}|_{C_i}=\mathfrak {D}_i$
. Let
![]() $R\in \sigma $
. If
$R\in \sigma $
. If
![]() $\vec {u}\in R^{\mathfrak {D}_i}$
then it follows immediately from the definition that
$\vec {u}\in R^{\mathfrak {D}_i}$
then it follows immediately from the definition that
![]() $\vec {u}\in R^{\mathfrak {D}}$
. On the other hand if
$\vec {u}\in R^{\mathfrak {D}}$
. On the other hand if
![]() $\vec {u}\in R^{\mathfrak {D}}\cap C_i^{\operatorname {ar}(R)}$
then by definition
$\vec {u}\in R^{\mathfrak {D}}\cap C_i^{\operatorname {ar}(R)}$
then by definition
![]() $\vec {u}\in R^{\mathfrak {D}_j}\cap C_i^{\operatorname {ar}(R)}$
for some
$\vec {u}\in R^{\mathfrak {D}_j}\cap C_i^{\operatorname {ar}(R)}$
for some
![]() $j\leq m$
. Then
$j\leq m$
. Then
![]() $\vec {u}\in C_j^{\operatorname {ar}(R)}\cap C_i^{\operatorname {ar}(R)}=C_{ij}^{\operatorname {ar}(R)}$
, and thus item (ii) implies that
$\vec {u}\in C_j^{\operatorname {ar}(R)}\cap C_i^{\operatorname {ar}(R)}=C_{ij}^{\operatorname {ar}(R)}$
, and thus item (ii) implies that
![]() $\vec {u}$
is also contained in the relation
$\vec {u}$
is also contained in the relation
![]() $R^{\mathfrak {D}_i}$
.
$R^{\mathfrak {D}_i}$
.
Claim 2.
![]() $\mathfrak {D}\in \operatorname {Age}(\mathfrak {A})$
. Let us assume that this is not the case. Then let
$\mathfrak {D}\in \operatorname {Age}(\mathfrak {A})$
. Let us assume that this is not the case. Then let
![]() $\mathfrak {D}'$
be a minimal substructure of
$\mathfrak {D}'$
be a minimal substructure of
![]() $\mathfrak {D}$
which is not in age
$\mathfrak {D}$
which is not in age
![]() $\operatorname {Age}(\mathfrak {A})$
. Then
$\operatorname {Age}(\mathfrak {A})$
. Then
![]() $|\mathfrak {D}'|\leq b(\mathfrak {A})=m$
. Therefore there exists some
$|\mathfrak {D}'|\leq b(\mathfrak {A})=m$
. Therefore there exists some
![]() $a_i,\ 0\leq i\leq m$
which is not contained in
$a_i,\ 0\leq i\leq m$
which is not contained in
![]() $\mathfrak {D}'$
. Then the domain set of
$\mathfrak {D}'$
. Then the domain set of
![]() $\mathfrak {D}'$
is contained in
$\mathfrak {D}'$
is contained in
![]() $C_i$
for some i, and thus
$C_i$
for some i, and thus
![]() $\mathfrak {D}'$
is substructure of
$\mathfrak {D}'$
is substructure of
![]() $\mathfrak {D}|_{C_i}=\mathfrak {D}_i$
. In particular
$\mathfrak {D}|_{C_i}=\mathfrak {D}_i$
. In particular
![]() $\mathfrak {D}'\in \operatorname {Age}(\mathfrak {A})$
, a contradiction.
$\mathfrak {D}'\in \operatorname {Age}(\mathfrak {A})$
, a contradiction.
Finally, let
![]() $\mathfrak {C}$
be the
$\mathfrak {C}$
be the
![]() $\tau $
-reduct of
$\tau $
-reduct of
![]() $\mathfrak {D}$
. Then
$\mathfrak {D}$
. Then
![]() $\mathfrak {C}\in \operatorname {Age}(\mathfrak {B})$
.
$\mathfrak {C}\in \operatorname {Age}(\mathfrak {B})$
.
Lemma 4.5. Let
![]() $\mathfrak {A}$
be an
$\mathfrak {A}$
be an
![]() $\omega $
-categorical structure with signature
$\omega $
-categorical structure with signature
![]() $\sigma $
, let
$\sigma $
, let
![]() $\tau \subseteq \sigma $
, and let
$\tau \subseteq \sigma $
, and let
![]() $\mathfrak {B}$
be the
$\mathfrak {B}$
be the
![]() $\tau $
-reduct of
$\tau $
-reduct of
![]() $\mathfrak {A}$
. Let
$\mathfrak {A}$
. Let ![]() . Then for every
. Then for every
![]() $\tau $
-type p which is realizable in
$\tau $
-type p which is realizable in
![]() $\mathfrak {B}$
there exist at most d many
$\mathfrak {B}$
there exist at most d many
![]() $\sigma $
-types q which are realizable in
$\sigma $
-types q which are realizable in
![]() $\mathfrak {A}$
and such that
$\mathfrak {A}$
and such that
![]() $p\subset q$
.
$p\subset q$
.
Proof Let ![]() with
with
![]() $|I|=d$
, and let us choose
$|I|=d$
, and let us choose
![]() $\vec {u}\in A^k$
with
$\vec {u}\in A^k$
with
![]() $\operatorname {tp}_{\mathfrak {B}}(\vec {u})=p$
. Then if
$\operatorname {tp}_{\mathfrak {B}}(\vec {u})=p$
. Then if
![]() $q\supset p$
then there exists some
$q\supset p$
then there exists some
![]() $\vec {v}\in A^k$
such that
$\vec {v}\in A^k$
such that
![]() $\operatorname {tp}_{\mathfrak {A}}(\vec {v})=q$
and
$\operatorname {tp}_{\mathfrak {A}}(\vec {v})=q$
and
![]() $\operatorname {tp}_{\mathfrak {B}}(\vec {v})=p=\operatorname {tp}_{\mathfrak {B}}(\vec {u})$
. By Lemma 4.1 the second condition holds if and only if
$\operatorname {tp}_{\mathfrak {B}}(\vec {v})=p=\operatorname {tp}_{\mathfrak {B}}(\vec {u})$
. By Lemma 4.1 the second condition holds if and only if
![]() $\vec {v}\approx _{\mathfrak {A}}\alpha _i(\vec {u})$
for some
$\vec {v}\approx _{\mathfrak {A}}\alpha _i(\vec {u})$
for some
![]() $i\in I$
. This implies that if
$i\in I$
. This implies that if
![]() $\operatorname {tp}_{\mathfrak {B}}(\vec {v})=p$
then
$\operatorname {tp}_{\mathfrak {B}}(\vec {v})=p$
then
![]() $q=\operatorname {tp}_{\mathfrak {A}}(\vec {v})=\operatorname {tp}_{\mathfrak {A}}(\sigma _i(\vec {u}))$
for some
$q=\operatorname {tp}_{\mathfrak {A}}(\vec {v})=\operatorname {tp}_{\mathfrak {A}}(\sigma _i(\vec {u}))$
for some
![]() $i\in I$
. This shows the statement of the lemma.
$i\in I$
. This shows the statement of the lemma.
Lemma 4.6. Let
![]() $\mathfrak {A}$
be a homogeneous finitely bounded structure with signature
$\mathfrak {A}$
be a homogeneous finitely bounded structure with signature
![]() $\sigma $
, and let
$\sigma $
, and let ![]() . Let
. Let
![]() $\tau \subset \sigma $
, and let
$\tau \subset \sigma $
, and let
![]() $\mathfrak {B}$
be a
$\mathfrak {B}$
be a
![]() $\tau $
-reduct of
$\tau $
-reduct of
![]() $\mathfrak {A}$
which is also homogeneous, and let us assume that
$\mathfrak {A}$
which is also homogeneous, and let us assume that ![]() is finite. Then
is finite. Then
![]() $b(\mathfrak {B})\leq md^{m+1}$
.
$b(\mathfrak {B})\leq md^{m+1}$
.
Proof Let
![]() $\mathfrak {C}\in \operatorname {Min}({\operatorname {Age}(\mathfrak {B})}^{c})$
. We have to show that
$\mathfrak {C}\in \operatorname {Min}({\operatorname {Age}(\mathfrak {B})}^{c})$
. We have to show that
![]() $|\mathfrak {C}|\leq md^{m+1}$
. Let
$|\mathfrak {C}|\leq md^{m+1}$
. Let
![]() $a_0,\dots ,a_m\in C$
, and let
$a_0,\dots ,a_m\in C$
, and let ![]() . Then
. Then
![]() $\mathfrak {C}_i\in \operatorname {Age}(\mathfrak {B})$
. Therefore there exist
$\mathfrak {C}_i\in \operatorname {Age}(\mathfrak {B})$
. Therefore there exist
![]() $\sigma $
-expansions
$\sigma $
-expansions
![]() $\mathfrak {D}_i$
of
$\mathfrak {D}_i$
of
![]() $\mathfrak {C}_i$
which are contained in
$\mathfrak {C}_i$
which are contained in
![]() $\operatorname {Age}(\mathfrak {A})$
. Let
$\operatorname {Age}(\mathfrak {A})$
. Let
![]() $\vec {u}_i$
be a tuple which enumerates all elements of
$\vec {u}_i$
be a tuple which enumerates all elements of
![]() $C_i$
. Let
$C_i$
. Let
![]() $\mathfrak {D}_{i0},\dots ,\mathfrak {D}_{i(l(i)-1)}$
be all the possible
$\mathfrak {D}_{i0},\dots ,\mathfrak {D}_{i(l(i)-1)}$
be all the possible
![]() $\sigma $
-expansions of
$\sigma $
-expansions of
![]() $\mathfrak {C}_i$
which are contained in
$\mathfrak {C}_i$
which are contained in
![]() $\operatorname {Age}(\mathfrak {A})$
. Then
$\operatorname {Age}(\mathfrak {A})$
. Then
![]() $\operatorname {tp}_{\mathfrak {D}_{ij}}(\vec {u})$
with
$\operatorname {tp}_{\mathfrak {D}_{ij}}(\vec {u})$
with
![]() $j<l(i)$
are pairwise different
$j<l(i)$
are pairwise different
![]() $\sigma $
-types all of which contain
$\sigma $
-types all of which contain
![]() $\operatorname {tp}_{\mathfrak {C}}(\vec {u})$
. Since
$\operatorname {tp}_{\mathfrak {C}}(\vec {u})$
. Since
![]() $\mathfrak {D}_{ij}\in \operatorname {Age}(\mathfrak {A})$
it follows that all
$\mathfrak {D}_{ij}\in \operatorname {Age}(\mathfrak {A})$
it follows that all
![]() $\sigma $
-types
$\sigma $
-types
![]() $\operatorname {tp}_{\mathfrak {D}_{ij}}(\vec {u})$
are realizable in
$\operatorname {tp}_{\mathfrak {D}_{ij}}(\vec {u})$
are realizable in
![]() $\mathfrak {A}$
. Therefore by Lemma 4.5 it follows that
$\mathfrak {A}$
. Therefore by Lemma 4.5 it follows that
![]() $l(i)< d$
for all
$l(i)< d$
for all
![]() $i\leq m$
.
$i\leq m$
.
Since
![]() $\mathfrak {C}\not \in \operatorname {Age}(\mathfrak {B})$
, and all
$\mathfrak {C}\not \in \operatorname {Age}(\mathfrak {B})$
, and all
![]() $\mathfrak {D}_{ij}$
with
$\mathfrak {D}_{ij}$
with
![]() $i\leq m, j<l(i)$
are in
$i\leq m, j<l(i)$
are in
![]() $\operatorname {Age}(\mathfrak {A})$
it follows by Lemma 4.4 that for all functions
$\operatorname {Age}(\mathfrak {A})$
it follows by Lemma 4.4 that for all functions
![]() $f\colon m+1\rightarrow d$
for which
$f\colon m+1\rightarrow d$
for which
![]() $f(i)\leq l(i)\colon i=0,\dots ,m$
we have
$f(i)\leq l(i)\colon i=0,\dots ,m$
we have
![]() $\mathfrak {D}_{if(i)}|_{C\setminus \{a_i,a_j\}}\neq \mathfrak {D}_{jf(j)}|_{C\setminus \{a_i,a_j\}}$
for some
$\mathfrak {D}_{if(i)}|_{C\setminus \{a_i,a_j\}}\neq \mathfrak {D}_{jf(j)}|_{C\setminus \{a_i,a_j\}}$
for some
![]() $i,j\leq m$
. This implies that for every function f as above there exist a tuple
$i,j\leq m$
. This implies that for every function f as above there exist a tuple
![]() $\vec {u}_f$
from
$\vec {u}_f$
from ![]() and an
and an
![]() $R_f\in \sigma $
such that
$R_f\in \sigma $
such that
![]() $\vec {u}_f\in R_f^{\mathfrak {D}_{if(i)}}\not \Leftrightarrow \vec {u}_f\in R_f^{\mathfrak {D}_{jf(j)}}$
. Now let
$\vec {u}_f\in R_f^{\mathfrak {D}_{if(i)}}\not \Leftrightarrow \vec {u}_f\in R_f^{\mathfrak {D}_{jf(j)}}$
. Now let
![]() $C'$
be the union of element in all tuples
$C'$
be the union of element in all tuples
![]() $\vec {u}_f$
. Then the length of the tuples
$\vec {u}_f$
. Then the length of the tuples
![]() $\vec {u}_f$
is at most
$\vec {u}_f$
is at most
![]() $m(\mathfrak {A})\leq b(\mathfrak {A})\leq m$
. Therefore
$m(\mathfrak {A})\leq b(\mathfrak {A})\leq m$
. Therefore
![]() $|C'|\leq md^{m+1}$
. Let
$|C'|\leq md^{m+1}$
. Let
![]() $\mathfrak {C}':=\mathfrak {C}|_{C'}$
.
$\mathfrak {C}':=\mathfrak {C}|_{C'}$
.
Now we show that
![]() $\mathfrak {C}'\not \in \operatorname {Age}(\mathfrak {B})\ (*)$
. Let us assume for contradiction that
$\mathfrak {C}'\not \in \operatorname {Age}(\mathfrak {B})\ (*)$
. Let us assume for contradiction that
![]() $\mathfrak {C}'\in \operatorname {Age}(\mathfrak {B})$
. Let
$\mathfrak {C}'\in \operatorname {Age}(\mathfrak {B})$
. Let
![]() $C_i':=C_i\setminus \{a_i\}$
,
$C_i':=C_i\setminus \{a_i\}$
,
![]() $C_{ij}':=C_i'\cap C_j'$
, and
$C_{ij}':=C_i'\cap C_j'$
, and
![]() $\mathfrak {C}_i':=\mathfrak {C}|_{C' \setminus \{a_i\}}$
. Then by applying Lemma 4.4 again it follows that there exist
$\mathfrak {C}_i':=\mathfrak {C}|_{C' \setminus \{a_i\}}$
. Then by applying Lemma 4.4 again it follows that there exist
![]() $\sigma $
-expansions
$\sigma $
-expansions
![]() $\mathfrak {D}^{\prime }_i$
of
$\mathfrak {D}^{\prime }_i$
of
![]() $\mathfrak {C}_i'$
such that
$\mathfrak {C}_i'$
such that
![]() $\mathfrak {D}_i'\in \operatorname {Age}(\mathfrak {A})$
, and
$\mathfrak {D}_i'\in \operatorname {Age}(\mathfrak {A})$
, and
![]() $\mathfrak {D}_i'|_{C_{ij}'}=\mathfrak {D}_j'|_{C_{ij}'}$
. It follows from the homogeneity of
$\mathfrak {D}_i'|_{C_{ij}'}=\mathfrak {D}_j'|_{C_{ij}'}$
. It follows from the homogeneity of
![]() $\mathfrak {B}$
that for all i there exists a
$\mathfrak {B}$
that for all i there exists a
![]() $\sigma $
-expansion
$\sigma $
-expansion
![]() $\mathfrak {D}_i"\in \operatorname {Age}(\mathfrak {A})$
of
$\mathfrak {D}_i"\in \operatorname {Age}(\mathfrak {A})$
of
![]() $\mathfrak {C}_i$
such that
$\mathfrak {C}_i$
such that
![]() $\mathfrak {D}_i"|_{C_i'}=\mathfrak {D}_i'$
. Then
$\mathfrak {D}_i"|_{C_i'}=\mathfrak {D}_i'$
. Then
![]() $\mathfrak {D}_i"=\mathfrak {D}_{if(i)}$
for some
$\mathfrak {D}_i"=\mathfrak {D}_{if(i)}$
for some
![]() $f(i)< l(i)$
for all i. This also implies that for all
$f(i)< l(i)$
for all i. This also implies that for all
![]() $i,j< m$
we also have
$i,j< m$
we also have ![]() . On the other hand by definition we know that there exist indices
. On the other hand by definition we know that there exist indices
![]() $i,j\leq m$
, a tuple
$i,j\leq m$
, a tuple
![]() $\vec {u}_f$
from
$\vec {u}_f$
from
![]() $C_{ij}$
, and a relational symbol
$C_{ij}$
, and a relational symbol
![]() $R_f$
such that
$R_f$
such that
![]() $\vec {u}_f\in R_f^{\mathfrak {D}_{if(i)}}\not \Leftrightarrow \vec {u}_f\in R_f^{\mathfrak {D}_{jf(j)}}$
. By the construction of
$\vec {u}_f\in R_f^{\mathfrak {D}_{if(i)}}\not \Leftrightarrow \vec {u}_f\in R_f^{\mathfrak {D}_{jf(j)}}$
. By the construction of
![]() $C'$
it follows that every coordinate of
$C'$
it follows that every coordinate of
![]() $\vec {u}_f$
is from
$\vec {u}_f$
is from
![]() $C'$
and then also from
$C'$
and then also from
![]() $C'\cap C_{ij}=C'\setminus \{a_i,a_j\}=C_{ij}'$
. Combining this with the observation that
$C'\cap C_{ij}=C'\setminus \{a_i,a_j\}=C_{ij}'$
. Combining this with the observation that
![]() $\mathfrak {D}_{if(i)}|_{C_i'}=\mathfrak {D}_i'$
it follows that
$\mathfrak {D}_{if(i)}|_{C_i'}=\mathfrak {D}_i'$
it follows that
![]() $R^{\mathfrak {D}_i'}(\vec {u}_f)\not \Leftrightarrow R^{\mathfrak {D}_j'}(\vec {u}_f)$
. This contradicts the equality
$R^{\mathfrak {D}_i'}(\vec {u}_f)\not \Leftrightarrow R^{\mathfrak {D}_j'}(\vec {u}_f)$
. This contradicts the equality ![]() , and thus finishes the proof of
, and thus finishes the proof of
![]() $(*)$
.
$(*)$
.
Since
![]() $\mathfrak {C}$
was chosen to be a minimal
$\mathfrak {C}$
was chosen to be a minimal
![]() $\tau $
-structure in
$\tau $
-structure in
![]() ${\operatorname {Age}(\mathfrak {B})}^{c}$
, the statement
${\operatorname {Age}(\mathfrak {B})}^{c}$
, the statement
![]() $(*)$
implies that in fact
$(*)$
implies that in fact
![]() $\mathfrak {C}=\mathfrak {C}'$
. Hence
$\mathfrak {C}=\mathfrak {C}'$
. Hence
![]() $|\mathfrak {C}|=|\mathfrak {C}'|\leq md^{m+1}$
which finishes the proof of the lemma.
$|\mathfrak {C}|=|\mathfrak {C}'|\leq md^{m+1}$
which finishes the proof of the lemma.
Lemma 4.7. Let
![]() $\mathfrak {A}$
be a homogeneous finitely bounded structure with
$\mathfrak {A}$
be a homogeneous finitely bounded structure with ![]() , and let
, and let
![]() $\mathfrak {B}$
be a reduct of
$\mathfrak {B}$
be a reduct of
![]() $\mathfrak {A}$
with
$\mathfrak {A}$
with
![]() $|\operatorname {Aut}(\mathfrak {B}):\operatorname {Aut}(\mathfrak {A})|=d$
. Then
$|\operatorname {Aut}(\mathfrak {B}):\operatorname {Aut}(\mathfrak {A})|=d$
. Then
![]() $\mathfrak {B}$
is interdefinable with a homogeneous structure
$\mathfrak {B}$
is interdefinable with a homogeneous structure
![]() $\mathfrak {B}'$
with
$\mathfrak {B}'$
with
![]() $b(\mathfrak {B}')\leq md^{dm+2}$
.
$b(\mathfrak {B}')\leq md^{dm+2}$
.
Proof Let ![]() . Then
. Then
![]() $\mathfrak {B}'$
is homogeneous, and it is interdefinable with
$\mathfrak {B}'$
is homogeneous, and it is interdefinable with
![]() $\mathfrak {B}$
by Lemmas 4.2 and 2.21. Let
$\mathfrak {B}$
by Lemmas 4.2 and 2.21. Let
![]() $\mathfrak {A}'$
be the structure
$\mathfrak {A}'$
be the structure
![]() $\mathfrak {A}$
expanded by all relations of
$\mathfrak {A}$
expanded by all relations of
![]() $\mathfrak {B}'$
. Then
$\mathfrak {B}'$
. Then
![]() $\mathfrak {A}$
and
$\mathfrak {A}$
and
![]() $\mathfrak {A}'$
are interdefinable, and thus
$\mathfrak {A}'$
are interdefinable, and thus
![]() $\operatorname {Aut}(\mathfrak {A})=\operatorname {Aut}(\mathfrak {A}')$
, and
$\operatorname {Aut}(\mathfrak {A})=\operatorname {Aut}(\mathfrak {A}')$
, and
![]() $\mathfrak {A}'$
is also homogeneous. Then by applying Lemma 4.6 to the structures
$\mathfrak {A}'$
is also homogeneous. Then by applying Lemma 4.6 to the structures
![]() $\mathfrak {A}'$
and
$\mathfrak {A}'$
and
![]() $\mathfrak {B}'$
we obtain
$\mathfrak {B}'$
we obtain
![]() $b(\mathfrak {B}')\leq (dm)d^{dm+1}=md^{dm+2}$
.
$b(\mathfrak {B}')\leq (dm)d^{dm+1}=md^{dm+2}$
.
Lemma 4.7 immediately implies the following.
Corollary 4.8. The class
![]() $\mathcal {FBH}$
is closed under taking finite-index reducts.
$\mathcal {FBH}$
is closed under taking finite-index reducts.
Theorem 4.9.
![]() $\mathcal {M}\subset \mathcal {FBH}$
.
$\mathcal {M}\subset \mathcal {FBH}$
.
5. Thomas’ conjecture for hereditarily cellular structures
In this section we show that Thomas’ conjecture holds for the class
![]() $\mathcal {M}$
, i.e., every structure in
$\mathcal {M}$
, i.e., every structure in
![]() $\mathcal {M}$
has finitely many reducts up to interdefinability.
$\mathcal {M}$
has finitely many reducts up to interdefinability.
Notation 5.1. For a permutation group H we denote by
![]() $\operatorname {acl}_H(\emptyset )$
the union of the finite orbits of H.
$\operatorname {acl}_H(\emptyset )$
the union of the finite orbits of H.
Remark 5.2. The notation
![]() $\operatorname {acl}$
stands for algebraic closure. For our discussion we only need to define it for the empty set.
$\operatorname {acl}$
stands for algebraic closure. For our discussion we only need to define it for the empty set.
Let
![]() $G\leq \operatorname {Sym}(X)$
be a permutation group. Then we define
$G\leq \operatorname {Sym}(X)$
be a permutation group. Then we define
![]() $w(G)$
to be the supremum of the set
$w(G)$
to be the supremum of the set
Lemma 5.3. If G is oligomorphic then
![]() $w(G)$
is finite.
$w(G)$
is finite.
Proof If x and y are in the same orbit of G then
 $$ \begin{align*} &\sup\{|\operatorname{acl}_{G_x/E}(\emptyset)|\colon E \text{ is a congruence of } G_x\}=\\&\sup\{|\operatorname{acl}_{G_y/E}(\emptyset)|\colon E \text{ is a congruence of } G_y\}. \end{align*} $$
$$ \begin{align*} &\sup\{|\operatorname{acl}_{G_x/E}(\emptyset)|\colon E \text{ is a congruence of } G_x\}=\\&\sup\{|\operatorname{acl}_{G_y/E}(\emptyset)|\colon E \text{ is a congruence of } G_y\}. \end{align*} $$
Therefore, since G has finitely many orbits, it is enough to show that
![]() $\sup \{|\operatorname {acl}_{G_x/E}(\emptyset )|\colon E \text { is a congruence of } G_x\}$
is finite for a fixed x. Since G is oligomorphic, so is
$\sup \{|\operatorname {acl}_{G_x/E}(\emptyset )|\colon E \text { is a congruence of } G_x\}$
is finite for a fixed x. Since G is oligomorphic, so is
![]() $G_x$
, in particular
$G_x$
, in particular
![]() $G_x$
has finitely many 2-orbits. Since all congruences of
$G_x$
has finitely many 2-orbits. Since all congruences of
![]() $G_x$
are unions of 2-orbits of
$G_x$
are unions of 2-orbits of
![]() $G_x$
, it also follows that
$G_x$
, it also follows that
![]() $G_x$
has finitely many congruences. Therefore it is enough to show that
$G_x$
has finitely many congruences. Therefore it is enough to show that
![]() $\operatorname {acl}_{G_x/E}(\emptyset )$
is finite for a fixed congruence E of
$\operatorname {acl}_{G_x/E}(\emptyset )$
is finite for a fixed congruence E of
![]() $G_x$
. Since
$G_x$
. Since
![]() $G_x$
is oligomorphic, so is
$G_x$
is oligomorphic, so is
![]() $G_x/E$
. In particular
$G_x/E$
. In particular
![]() $G_x/E$
has finitely many finite orbits, and therefore
$G_x/E$
has finitely many finite orbits, and therefore
![]() $\operatorname {acl}_{G_x/E}(\emptyset )$
is finite.
$\operatorname {acl}_{G_x/E}(\emptyset )$
is finite.
Lemma 5.4. If
![]() $G\leq H$
then
$G\leq H$
then
![]() $w(G)\geq w(H)$
.
$w(G)\geq w(H)$
.
Proof If E is a congruence of
![]() $H_x$
for some
$H_x$
for some
![]() $x\in X$
then it is also a congruence of
$x\in X$
then it is also a congruence of
![]() $G_x$
, and
$G_x$
, and
![]() $G_x/E\leq H_x/E$
. Therefore in this case
$G_x/E\leq H_x/E$
. Therefore in this case
![]() $\operatorname {acl}_{H_x/E}(\emptyset )\leq \operatorname {acl}_{G_x/E}(\emptyset )$
. Taking the supremum over x and the congruences E of
$\operatorname {acl}_{H_x/E}(\emptyset )\leq \operatorname {acl}_{G_x/E}(\emptyset )$
. Taking the supremum over x and the congruences E of
![]() $H_x$
the claim of the lemma follows.
$H_x$
the claim of the lemma follows.
Lemma 5.5. Let
![]() $G_1,\dots ,G_k$
be permutation groups with pairwise disjoint domains, and let
$G_1,\dots ,G_k$
be permutation groups with pairwise disjoint domains, and let ![]() . Then
. Then
![]() $w(G)\leq \sum _{i=1}^kw(G_i)$
.
$w(G)\leq \sum _{i=1}^kw(G_i)$
.
Proof Let ![]() and
and ![]() . Let
. Let
![]() $x\in X_i$
, and let E be a congruence of
$x\in X_i$
, and let E be a congruence of
![]() $G_x$
. Let
$G_x$
. Let
![]() $\{[y_1]_E,\dots ,[y_m]_E\}$
be a finite orbit of
$\{[y_1]_E,\dots ,[y_m]_E\}$
be a finite orbit of
![]() $G_x/E$
for some
$G_x/E$
for some
![]() $y_1,\dots ,y_m$
with
$y_1,\dots ,y_m$
with
![]() $y_1\in X_i$
. Then since
$y_1\in X_i$
. Then since
![]() $G_x$
fixes the sets
$G_x$
fixes the sets
![]() $X_1,\dots ,X_k$
it follows that we can find
$X_1,\dots ,X_k$
it follows that we can find
![]() $y_1',\dots ,y_m'\in X_i$
such that
$y_1',\dots ,y_m'\in X_i$
such that
![]() $[y_l']_E=[y_l]_E$
for all
$[y_l']_E=[y_l]_E$
for all
![]() $l=1,\dots ,m$
. Then
$l=1,\dots ,m$
. Then
![]() $\{[y_1']_{E_i},\dots ,[y_m']_{E_i}\}$
is a finite orbit of
$\{[y_1']_{E_i},\dots ,[y_m']_{E_i}\}$
is a finite orbit of
![]() $(G_x|_{X_i})/E_i$
for
$(G_x|_{X_i})/E_i$
for ![]() . This implies that
. This implies that
![]() $\operatorname {acl}_{G_x/E}(\emptyset )$
can be written as a union of
$\operatorname {acl}_{G_x/E}(\emptyset )$
can be written as a union of
![]() $\operatorname {acl}_{(G_x)|_{X_j}/E_j}(\emptyset )\colon j=1\dots ,k$
. Since
$\operatorname {acl}_{(G_x)|_{X_j}/E_j}(\emptyset )\colon j=1\dots ,k$
. Since ![]() it follows that
it follows that
![]() $G_x|_{X_j}=G_j$
if
$G_x|_{X_j}=G_j$
if
![]() $j\neq i$
, and
$j\neq i$
, and
![]() $G_x|_{X_j}=G_i|_x$
if
$G_x|_{X_j}=G_i|_x$
if
![]() $j=1$
. Let
$j=1$
. Let
![]() $x_j\in X_j$
be arbitrary with
$x_j\in X_j$
be arbitrary with
![]() $x_i=x$
. Then since
$x_i=x$
. Then since
![]() $(G_j)_{x_j}\leq (G_x)|_{X_j}$
for all j, it follows that
$(G_j)_{x_j}\leq (G_x)|_{X_j}$
for all j, it follows that
![]() $\operatorname {acl}_{(G_x)|_{X_j}/E_j}(\emptyset )\subset \operatorname {acl}_{(G_j)_{x_j}/E_j}(\emptyset )$
, and thus
$\operatorname {acl}_{(G_x)|_{X_j}/E_j}(\emptyset )\subset \operatorname {acl}_{(G_j)_{x_j}/E_j}(\emptyset )$
, and thus
![]() $|\operatorname {acl}_{(G_x)|_{X_j}/E_j}(\emptyset )|\leq w(G_j)$
. Therefore
$|\operatorname {acl}_{(G_x)|_{X_j}/E_j}(\emptyset )|\leq w(G_j)$
. Therefore
![]() $|\operatorname {acl}_{G_x/E}(\emptyset )|\leq \sum _{i=1}^kw(G_i)$
. Since this holds for every
$|\operatorname {acl}_{G_x/E}(\emptyset )|\leq \sum _{i=1}^kw(G_i)$
. Since this holds for every
![]() $x\in X$
, and a congruence E of
$x\in X$
, and a congruence E of
![]() $G_x$
we obtain
$G_x$
we obtain
![]() $w(G)\leq \sum _{i=1}^kw(G_i)$
.
$w(G)\leq \sum _{i=1}^kw(G_i)$
.
Lemma 5.6. Let
![]() $Y_0,\dots ,Y_k,Y,N_0,\dots ,N_k,N,H$
be as in Section 3.1. Let
$Y_0,\dots ,Y_k,Y,N_0,\dots ,N_k,N,H$
be as in Section 3.1. Let ![]() . Then
. Then
![]() $w(H_i)\leq w(\mathcal {G}(H;N_0,\dots ,N_k))$
for all
$w(H_i)\leq w(\mathcal {G}(H;N_0,\dots ,N_k))$
for all
![]() $i=0,1,\dots ,k$
.
$i=0,1,\dots ,k$
.
Proof In this proof we use the notations from Section 3.1.
Let ![]() . We have to show that for all
. We have to show that for all
![]() $x\in Y$
and a congruence E of
$x\in Y$
and a congruence E of
![]() $(H_i)_x$
we have
$(H_i)_x$
we have
![]() $|\operatorname {acl}_{(H_i)_x/E}(\emptyset )|\leq w(G)$
.
$|\operatorname {acl}_{(H_i)_x/E}(\emptyset )|\leq w(G)$
.
Let us assume that
![]() $x\in Y_0$
. Then
$x\in Y_0$
. Then
![]() $\operatorname {acl}_G(\emptyset )=Y_0$
, and thus
$\operatorname {acl}_G(\emptyset )=Y_0$
, and thus
![]() $w(G)\geq |Y_0|$
. On the other hand
$w(G)\geq |Y_0|$
. On the other hand
![]() $w((H_0)_x)\leq |\operatorname {Dom}(H_0)|=|Y_0|$
. Therefore the statement of the lemma if true for
$w((H_0)_x)\leq |\operatorname {Dom}(H_0)|=|Y_0|$
. Therefore the statement of the lemma if true for
![]() $i=0$
.
$i=0$
.
Let
![]() $x\in Y_i$
for
$x\in Y_i$
for
![]() $i>0$
, and let E be a congruence of
$i>0$
, and let E be a congruence of
![]() $(H_i)_x$
. Let
$(H_i)_x$
. Let
![]() $E^*$
the equivalence relation on X whose equivalence classes are:
$E^*$
the equivalence relation on X whose equivalence classes are:
-
(a)
 $Y_0\times \{0\}$
,
$Y_0\times \{0\}$
, -
(b) all
 $\nabla $
-classes except
$\nabla $
-classes except
 $Y_i\times \omega $
,
$Y_i\times \omega $
, -
(c) all
 $\Delta $
-classes in
$\Delta $
-classes in
 $Y_i$
except
$Y_i$
except
 $Y_i\times \{0\}$
,
$Y_i\times \{0\}$
, -
(d) the set of the form
 $C\times \{0\}$
where
$C\times \{0\}$
where
 $C\in Y_i/E$
.
$C\in Y_i/E$
.
We claim that
![]() $E^*$
is a congruence of
$E^*$
is a congruence of
![]() $G_{(x,0)}$
. Since
$G_{(x,0)}$
. Since
![]() $G_{(x,0)}$
preserves the relations
$G_{(x,0)}$
preserves the relations
![]() $\nabla $
and
$\nabla $
and
![]() $\Delta $
it follows that G maps every
$\Delta $
it follows that G maps every
![]() $E^*$
class corresponding to cases (a)–(d) to another class corresponding to the same item. Let
$E^*$
class corresponding to cases (a)–(d) to another class corresponding to the same item. Let
![]() $C\in Y_i/E_x$
, and let
$C\in Y_i/E_x$
, and let
![]() $\sigma \in G_{(x,0)}$
. We have to show that
$\sigma \in G_{(x,0)}$
. We have to show that
![]() $\sigma $
maps
$\sigma $
maps
![]() $C\times \{0\}$
to
$C\times \{0\}$
to
![]() $C'\times \{0\}$
for some
$C'\times \{0\}$
for some
![]() $C'\in Y_i/E_x$
. Let
$C'\in Y_i/E_x$
. Let
![]() $\vec {0}:=(0,\dots ,0)$
. Then by definition
$\vec {0}:=(0,\dots ,0)$
. Then by definition
![]() $\rho _{\vec {0}}(\sigma )\in H$
. Since
$\rho _{\vec {0}}(\sigma )\in H$
. Since
![]() $G_{(x,0)}$
preserves
$G_{(x,0)}$
preserves
![]() $(x,0)$
and the relation
$(x,0)$
and the relation
![]() $\Delta $
it follows that
$\Delta $
it follows that
![]() $\sigma $
preserves
$\sigma $
preserves
![]() $[(x,0)]_{\Delta }=Y_i\times \{0\}$
. Therefore
$[(x,0)]_{\Delta }=Y_i\times \{0\}$
. Therefore ![]() for all
for all
![]() $a\in Y_i$
. This also implies that
$a\in Y_i$
. This also implies that
![]() $\rho _{\vec {0}}(\sigma )\in Y_i$
, and thus
$\rho _{\vec {0}}(\sigma )\in Y_i$
, and thus
![]() $\sigma ':=\rho _{\vec {0}}(\sigma )|_{Y_i}\in H_{(Y_i)}=H_i$
. Since
$\sigma ':=\rho _{\vec {0}}(\sigma )|_{Y_i}\in H_{(Y_i)}=H_i$
. Since
![]() $\sigma ((x,0))=(x,0)$
we have
$\sigma ((x,0))=(x,0)$
we have
![]() $\sigma '(x)=x$
. Then
$\sigma '(x)=x$
. Then ![]() since E is a congruence of
since E is a congruence of
![]() $(H_i)_x$
, and thus
$(H_i)_x$
, and thus
This shows that
![]() $E^*$
is a congruence of
$E^*$
is a congruence of
![]() $G_{(x,0)}$
.
$G_{(x,0)}$
.
The definition of
![]() $E^*$
implies that
$E^*$
implies that
![]() $\operatorname {acl}_{(H_i)_x/E}(\emptyset )\times \{0\}\subset \operatorname {acl}_{G_{(x,0)}/E^*}(\emptyset )$
, and thus
$\operatorname {acl}_{(H_i)_x/E}(\emptyset )\times \{0\}\subset \operatorname {acl}_{G_{(x,0)}/E^*}(\emptyset )$
, and thus
![]() $|\operatorname {acl}_{(H_i)_x/E}(\emptyset )|\leq |\operatorname {acl}_{G_{(x,0)}/E^*}(\emptyset )|\leq w(G)$
which finishes the proof of the lemma.
$|\operatorname {acl}_{(H_i)_x/E}(\emptyset )|\leq |\operatorname {acl}_{G_{(x,0)}/E^*}(\emptyset )|\leq w(G)$
which finishes the proof of the lemma.
Lemma 5.7. Let
![]() $N_0,\dots ,N_k,N,H\in \mathcal {H}$
be as in Definition 3.21, and let
$N_0,\dots ,N_k,N,H\in \mathcal {H}$
be as in Definition 3.21, and let
![]() $H_i:=H_{(Y_i)}$
. Then the group
$H_i:=H_{(Y_i)}$
. Then the group
![]() $H^*:=\langle H, \prod _{i=0}^kH_i\rangle $
is closed, and N is a finite index normal subgroup of
$H^*:=\langle H, \prod _{i=0}^kH_i\rangle $
is closed, and N is a finite index normal subgroup of
![]() $H^*$
.
$H^*$
.
Proof By our assumption N is a normal subgroup of H; therefore, it is enough to show that N is normalized by
![]() $\prod _{i=0}^kH_i$
. Since
$\prod _{i=0}^kH_i$
. Since
![]() $N\triangleleft H$
it follows that
$N\triangleleft H$
it follows that
![]() $\operatorname {id}(Y_0)\times \dots \times \operatorname {id}(Y_{i-1})\times N_i \times \operatorname {id}(Y_{i+1})\dots \times \operatorname {id}(Y_k)$
is normalized by
$\operatorname {id}(Y_0)\times \dots \times \operatorname {id}(Y_{i-1})\times N_i \times \operatorname {id}(Y_{i+1})\dots \times \operatorname {id}(Y_k)$
is normalized by
![]() $H|_{\{Y_i\}}$
. Therefore
$H|_{\{Y_i\}}$
. Therefore
![]() $N_i$
is normalized by
$N_i$
is normalized by
![]() $H_i$
, and thus
$H_i$
, and thus
![]() $N=\prod _{i=1}^kN_i$
is normalized by
$N=\prod _{i=1}^kN_i$
is normalized by
![]() $\prod _{i=0}^kH_i$
. This also means that
$\prod _{i=0}^kH_i$
. This also means that
![]() $N\triangleleft \overline {H^*}$
. By Corollary 3.36 this implies that
$N\triangleleft \overline {H^*}$
. By Corollary 3.36 this implies that
![]() $|H^*:N|\leq |\overline {H^*}:N|<\infty $
, and thus
$|H^*:N|\leq |\overline {H^*}:N|<\infty $
, and thus
![]() $H^*$
is closed.
$H^*$
is closed.
Lemma 5.8. Let
![]() $n,m\in \omega $
. Then there exist finitely many closed groups
$n,m\in \omega $
. Then there exist finitely many closed groups
![]() $G\in \mathcal {H}_n$
with
$G\in \mathcal {H}_n$
with
![]() $w(G)\leq m$
up to isomorphism.
$w(G)\leq m$
up to isomorphism.
Proof We prove the lemma by induction on n. For
![]() $n=-1$
there is nothing to show.
$n=-1$
there is nothing to show.
For the induction step let us consider a group
![]() $G\in \mathcal {H}_n$
with
$G\in \mathcal {H}_n$
with
![]() $w(G)\leq m$
for some
$w(G)\leq m$
for some
![]() $m\in \omega $
. By Theorem 3.41 we know that G is isomorphic to some group
$m\in \omega $
. By Theorem 3.41 we know that G is isomorphic to some group
![]() $\mathcal {G}(H;N_0,\dots ,N_k)$
where
$\mathcal {G}(H;N_0,\dots ,N_k)$
where
![]() $N_0,N_1,\dots ,N_k,H\in \mathcal {H}_{n-1}$
. Let
$N_0,N_1,\dots ,N_k,H\in \mathcal {H}_{n-1}$
. Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Then
. Then
![]() $\Delta ^*$
is a congruence of G, and
$\Delta ^*$
is a congruence of G, and
![]() $\operatorname {Dom}(G/\Delta ^*)\geq k+1$
. Therefore
$\operatorname {Dom}(G/\Delta ^*)\geq k+1$
. Therefore
![]() $k+1\leq w(G)=m$
. By Lemma 5.7 we know that
$k+1\leq w(G)=m$
. By Lemma 5.7 we know that
![]() $N\triangleleft H^*$
and
$N\triangleleft H^*$
and
![]() $H^*$
is closed. Hence
$H^*$
is closed. Hence
![]() $H^*\in \mathcal {H}_{n-1}$
. By Lemma 5.6 it follows that
$H^*\in \mathcal {H}_{n-1}$
. By Lemma 5.6 it follows that
![]() $w(H_i)\leq m$
, and then Lemma 5.5 implies
$w(H_i)\leq m$
, and then Lemma 5.5 implies
![]() $w(\prod _{i=0}^kH_i)\leq m(k+1)$
. By Lemma 5.4 we have
$w(\prod _{i=0}^kH_i)\leq m(k+1)$
. By Lemma 5.4 we have
![]() $w(H^*)\leq w(\prod _{i=0}^kH_i)$
; therefore,
$w(H^*)\leq w(\prod _{i=0}^kH_i)$
; therefore,
![]() $w(H^*)\leq m(k+1)\leq m^2$
. By the induction hypothesis this implies that we have finitely many choices for the group
$w(H^*)\leq m(k+1)\leq m^2$
. By the induction hypothesis this implies that we have finitely many choices for the group
![]() $H^*$
up to isomorphism. This means that it is enough to show that for a fixed group
$H^*$
up to isomorphism. This means that it is enough to show that for a fixed group
![]() $H^*\in \mathcal {H}_{n-1}$
we have finitely many choices for groups N and H in
$H^*\in \mathcal {H}_{n-1}$
we have finitely many choices for groups N and H in
![]() $\mathcal {H}_{n-1}$
such that
$\mathcal {H}_{n-1}$
such that
![]() $N\triangleleft H^*$
and
$N\triangleleft H^*$
and
![]() $H\leq H^*$
. By Corollary 3.36 we know that we have finitely many possible choices for the group N, and in all cases
$H\leq H^*$
. By Corollary 3.36 we know that we have finitely many possible choices for the group N, and in all cases
![]() $|H^*:N|$
is finite. Therefore if both
$|H^*:N|$
is finite. Therefore if both
![]() $H^*$
and N are fixed then we have finitely many choices for
$H^*$
and N are fixed then we have finitely many choices for
![]() $N\leq H\leq H^*$
. This finishes the proof of the lemma.
$N\leq H\leq H^*$
. This finishes the proof of the lemma.
Corollary 5.9.
![]() $\mathcal {H}$
contains countable many groups up to isomorphism.
$\mathcal {H}$
contains countable many groups up to isomorphism.
Proof Direct consequence of Lemma 5.8.
Remark 5.10. By Theorem 2.1 in [Reference Hrushovski30] we know that every
![]() $\omega $
-stable
$\omega $
-stable
![]() $\omega $
-categorical structure is interdefinable with a structure which has a finite signature and which is quasi-finitely axiomatizable. This also implies Corollary 5.9.
$\omega $
-categorical structure is interdefinable with a structure which has a finite signature and which is quasi-finitely axiomatizable. This also implies Corollary 5.9.
Now we can show that Thomas’ conjecture holds for the class
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Theorem 5.11. Every hereditarily cellular structure has finitely many reducts up to interdefinability.
Proof Let
![]() $\mathfrak {A}\in \mathcal {M}$
. We will check condition (5) of Proposition 2.17 for
$\mathfrak {A}\in \mathcal {M}$
. We will check condition (5) of Proposition 2.17 for
![]() $\mathfrak {A}$
. Let
$\mathfrak {A}$
. Let ![]() . Then
. Then
![]() $G\in \mathcal {H}$
by Theorem 3.6, and thus
$G\in \mathcal {H}$
by Theorem 3.6, and thus
![]() $G\in \mathcal {H}_n$
for some
$G\in \mathcal {H}_n$
for some
![]() $n\in \omega $
. Let
$n\in \omega $
. Let ![]() . Then for every closed supergroup H we have
. Then for every closed supergroup H we have
![]() $H\in \mathcal {H}_n$
and
$H\in \mathcal {H}_n$
and
![]() $w(H)\leq m$
by Lemma 5.4. Therefore by Lemma 5.8 we have finitely many choices for H up to isomorphism.
$w(H)\leq m$
by Lemma 5.4. Therefore by Lemma 5.8 we have finitely many choices for H up to isomorphism.
Remark 5.12. We know by Theorem 4.9 (or by the results of [Reference Lachlan34]) that all structures in
![]() $\mathcal {M}$
are finitely homogenizable. This implies that Theorem 5.11 is indeed a special case of Thomas’ conjecture.
$\mathcal {M}$
are finitely homogenizable. This implies that Theorem 5.11 is indeed a special case of Thomas’ conjecture.
Acknowledgments
I would like to thank Andrés Aranda for a careful reading and useful feedback on earlier versions of this article, and Manuel Bodirsky for discussion and helpful comments.
Funding
The author has received funding from the European Research Council (Grant Agreement No. 681988, CSP-Infinity). The research of the author was supported by the grants TKP2021-NVA-09 of the Ministry for Innovation and Technology, Hungary, and NKFIH-K138892.