Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-17T01:36:57.930Z Has data issue: false hasContentIssue false
  • English
  • Français

A characterization of the δ20 hyperhyperimmune sets

Published online by Cambridge University Press:  12 March 2014

Roland Sh. Omanadze  and
Andrea Sorbi
Roland Sh. Omanadze
Affiliation:
Javakhishvili Tbilisi State University, Tbilisi 0186., Georgia, E-mail: [email protected]
Andrea Sorbi
Affiliation:
Dipartimento di Scienze Matematiche ed Informatiche “R. Magari”, Università di Siena. 53100 Siena, Italy, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let A be an infinite 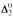set and let K be creative: we show that K ≤QA if and only if K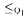A. (Here ≤Q denotes Q-reducibility, and 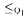is the subreducibility of ≤Q obtained by requesting that Q-reducibility be provided by a computable function f such that Wf(x) ∩ Wf(y) = ∅. if x ≠ y.) Using this result we prove that A is hyperhyperimmune if and only if no 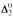subset B of A is s-complete, i.e., there is no 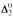subset B of A such that 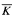≤sB, where ≤s denotes s-reducibility, and 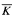denotes the complement of K.

Keywords

Q-reducibilitys-reducibilityhyperhyperimmune set
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 4 , December 2008 , pp. 1407 - 1415
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cooper, S. B., Enumeration reducibility, nondeterministic computations and relative computability of partial functions, Recursion theory week, Oberwolfach 1989 (Ambos-Spies, K., Müller, G., and Sacks, G. E., editors), Lecture Notes in Mathematics, vol. 1432, Springer–Verlag, Heidelberg, 1990, pp. 57–110.Google Scholar
[2]Friedberg, R. M. and Rogers, H. Jr., Reducibility and completeness for sets of integers, Zeitschrift für Mathematische Logik and Grundlagen der Mathematik, vol. 5 (1959), pp. 117–125.CrossRefGoogle Scholar
[3]Gill, J. T. III and Morris, P. H., On subcreative sets and S-reducibility, this Journal, vol. 39 (1974), no. 4, pp. 669–677.Google Scholar
[4]Jockusch, C. G. Jr., The degrees of hyperhyperimmune sets, this Journal, vol. 34 (1969), no. 3, pp. 489–493.Google Scholar
[5]McEvoy, K., The structure of the enumeration degrees, Ph.D. thesis, School of Mathematics, University of Leeds, 1984.Google Scholar
[6]Morley, M. and Soare, R. I., Splitting theorems and δ20 sets, Fundamenta Mathematicae, vol. 90 (1975), pp. 45–52.CrossRefGoogle Scholar
[7]Omanauze, R. Sh. and Sorbi, A., Strong enumeration reducibilities, Archive for Mathematical Logic, vol. 45 (2006), no. 7. pp. 869–912.CrossRefGoogle Scholar
[8]Rogers, H. Jr., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[9]Rozinas, M. G., Partial degrees of immune and hyperimmune sets, Siberian Mathematical Journal, vol. 19 (1978), pp. 613–616.CrossRefGoogle Scholar
[10]Soare, R. I., Recursively enumerable sets and degrees, Perspectives in Mathematical Logic, Omega Series, Springer–Verlag, Heidelberg, 1987.CrossRefGoogle Scholar
[11]Solov'ev, V. D., Q-reducibility and hyperhypersimple sets, Veroyatn. Metod. i Kibern., vol. 10-11 (1974), p. 1974, Russian.Google Scholar