Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-15T19:23:29.309Z Has data issue: false hasContentIssue false
  • English
  • Français

A characterization of the 0-basis homogeneous bounding degrees

Published online by Cambridge University Press:  12 March 2014

Karen Lange
Karen Lange*
Affiliation:
Mathematics Department, University of Notre Dame, 255 Hurley Hall, Notre Dame, In 46556-4618, USA. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We say a countable model 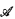has a 0-basis if the types realized in 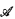are uniformly computable. We say 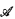has a (d-)decidable copy if there exists a model 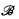≅ 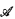such that the elementary diagram of 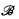is (d-)computable. Goncharov, Millar, and Peretyat'kin independently showed there exists a homogeneous model 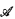with a 0-basis but no decidable copy. We extend this result here. Let d ≤ 0′ be any low2 degree. We show that there exists a homogeneous model 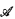with a 0-basis but no d-decidable copy. A degree d is 0-basis homogeneous bounding if any homogenous 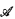with a 0-basis has a d-decidable copy. In previous work, we showed that the non low2 Δ20 degrees are 0-basis homogeneous bounding. The result of this paper shows that this is an exact characterization of the 0-basis homogeneous bounding Δ20 degrees.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 75 , Issue 3 , September 2010 , pp. 971 - 995
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ash, C.J. and Knight, J.F., Computable structures and the hyperarithmetical hierarchy, 1st ed., Studies in Logic and the Foundations of Mathematics, vol. 144, Amsterdam, 2000.Google Scholar
[2]Chang, C.C. and Keisler, H.J., Model theory, 3rd ed., Studies in Logic and the Foundations of Mathematics, vol. 73, North-Holland, Amsterdam, 1990, 1st edn. 1973, 2nd edn. 1977.Google Scholar
[3]Csima, B.F., Degree spectra of prime models, this Journal, vol. 69 (2004), pp. 430–442.Google Scholar
[4]Csima, B.F., Harizanov, V.S., Hirschfeldt, D.R., and Soare, R.I., Bounding homogeneous models, this Journal, vol. 72 (2007), pp. 305–323.Google Scholar
[5]Csima, B.F., Hirschfeldt, D.R., Knight, J.F., and Soare, R.I., Bounding prime models, this Journal, vol. 69 (2004), pp. 1117–1142.Google Scholar
[6]Epstein, R., Prime models of computably enumerable degree, this Journal, vol. 73 (2008), pp. 1373–1388.Google Scholar
[7]Goncharov, S.S., Strong constructivizability of homogeneous models (Russian), Algebra i Logika, vol. 17 (1978), pp. 363–388, 490, translated in: Algebra and Logic, vol. 17 (1978) pp. 247–263.Google Scholar
[8]Harizanov, V. S., Pure computable model theory, Handbook of recursive mathematics (Ershov, Yu.L., Goncharov, S.S., Nerode, A., and Remmel, J.B., editors), Studies in Logic and the Foundations of Mathematics, vol. 138-139, Elsevier Science, Amsterdam, 1998, pp. 3–114.Google Scholar
[9]Hirschfeldt, D.R., Lange, K.M., and Shore, R.A., The homogeneous model theorem, in preparation.Google Scholar
[10]Hirschfeldt, D.R., Shore, R.A., and Slaman, T. A., The atomic model theorem and type omitting, Transactions of American Mathematical Society, vol. 361 (2009), pp. 5805–5837.CrossRefGoogle Scholar
[11]Hirshfeldt, D.R., Computable trees, prime models, and relative decidability, Proceedings of the American Mathematical Society, vol. 134 (2006), pp. 1495–1498.CrossRefGoogle Scholar
[12]Jockusch, C. G. Jr., Degrees in which the recursive sets are uniformly recursive, Canadian Journal of Mathematics, vol. 24 (1972), pp. 1092–1099.CrossRefGoogle Scholar
[13]Knight, J. F., Degrees coded in jumps of orderings, this Journal, vol. 51 (1986), pp. 1034–1042.Google Scholar
[14]Lange, K. M., The degree spectra of homogeneous models, this Journal, vol. 73 (2008), pp. 1009–1028.Google Scholar
[15]Lange, K.M. and Soare, R.I., Computability of homogeneous models, Notre Dame Journal of Formal Logic, vol. 48 (2007), no. 1, pp. 143–170.CrossRefGoogle Scholar
[16]Marker, D., Model theory: An introduction, Graduate Texts in Mathematics, vol. 217, Springer-Verlag, 2002.Google Scholar
[17]Millar, T.S., Foundations of recursive model theory, Annals of Mathematical Logic, vol. 13 (1978), pp. 45–72.CrossRefGoogle Scholar
[18]Millar, T.S., Homogeneous models and decidability, Pacific Journal of Mathematics, vol. 91 (1980), pp. 407–418.CrossRefGoogle Scholar
[19]Peretyat'kin, M.G., A criterion for strong constructivizability of a homogeneous model (Russian), Algebra i Logika, vol. 17 (1978), pp. 436–454, 491, translated in: Algebra and Logic, vol. 19 (1980) pp. 202–229.Google Scholar
[20]Soare, R. I., Recursively enumerable sets and degrees; A study of computable functions and computably generated sets, Springer-Verlag, Heidelberg, 1987.Google Scholar
[21]Soare, R. I., Computability theory and applications, Springer-Verlag, Heidelberg, in preparation.Google Scholar