Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T12:29:46.464Z Has data issue: false hasContentIssue false
  • English
  • Français

The characteristic sequence of a first-order formula

Published online by Cambridge University Press:  12 March 2014

M. E. Malliaris
M. E. Malliaris*
Affiliation:
Group in Logic, University of California at Berkeley, 910 Evans Hall, Berkeley, CA 94720, USA. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a first-order formula φ(x; y) we introduce and study the characteristic sequence (Pn: n < ω) of hypergraphs defined by 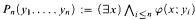. We show that combinatorial and classification theoretic properties of the characteristic sequence reflect classification theoretic properties of φ and vice versa. The main results are a characterization of NIP and of simplicity in terms of persistence of configurations in the characteristic sequence. Specifically, we show that some tree properties are detected by the presence of certain combinatorial configurations in the characteristic sequence while other properties such as instability and the independence property manifest themselves in the persistence of complicated configurations under localization.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 75 , Issue 4 , December 2010 , pp. 1415 - 1440
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Buechler, , Lascar strong types in some simple theories, this Journal, vol. 64 (1999), no. 2, pp. 817–824.Google Scholar
[2]Džamonja, and Shelah, , On ⊲*-maximality, Annals of Pure and Applied Logic, vol. 125 (2004), pp. 119–158.CrossRefGoogle Scholar
[3]Hrushovski, , Peterzil, , and Pillay, , Groups, measures, and the NIP, Journal of the American Mathematical Society, vol. 21 (2008), no. 2, pp. 563–596.CrossRefGoogle Scholar
[4]Keisler, , Ultraproducts which are not saturated, this Journal, vol. 32 (1967), pp. 23–46.Google Scholar
[5]Kim, and Pillay, , From stability to simplicity. The Bulletin of Symbolic Logic, vol. 4 (1998), no. 1, pp. 17–36.CrossRefGoogle Scholar
[6]Malliaris, , Persistence and regularity in unstable model theory, Ph.D. thesis, University of California, Berkeley, 2009.Google Scholar
[7]Malliaris, , Realization of φ-types and Keisler's order, Annals of Pure and Applied Logic, vol. 157 (2009), pp. 220–224.CrossRefGoogle Scholar
[8]Shelah, , Classification theory and the number of non-isomorphic models, revised ed., North-Holland, 1990.Google Scholar
[9]Shelah, , Toward classifying unstable theories, Annals of Pure and Applied Logic, vol. 80 (1996), pp. 229–255.CrossRefGoogle Scholar
[10]Shelah, , Classification theory for elementary classes with the dependence property—a modest beginning, Scientiae Mathematicae Japonicae, vol. 59 (2004), pp. 265–316, special issue on set theory and algebraic model theory.Google Scholar
[11]Shelah, , Dependent theories and the generic pair conjecture, arXiv:math.L0/0702292, 2008.Google Scholar
[12]Shelah, and Usvyatsov, , More on SOP1and SOP2, Annals of Pure and Applied Logic, vol. 155 (2008), no. 1, pp. 16–31.CrossRefGoogle Scholar
[13]Usvyatsov, , On generically stable types in dependent theories, this Journal, vol. 74 (2009), pp. 216–250.Google Scholar
[14]Wagner, , Simple theories, Mathematics and Its Applications 503, Kluwer Academic Publishers, 2000.CrossRefGoogle Scholar