CHAITIN’S Ω AS A CONTINUOUS FUNCTION

Abstract

We prove that the continuous function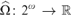${\rm{\hat \Omega }}:2^\omega \to $ that is defined via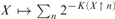$X \mapsto \mathop \sum \limits_n 2^{ - K\left( {Xn} \right)} $ for all 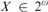$X \in {2^\omega }$ is differentiable exactly at the Martin-Löf random reals with the derivative having value 0; that it is nowhere monotonic; and that 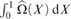$\mathop \smallint \nolimits _0^1{\rm{\hat{\Omega }}}\left( X \right)\,{\rm{d}}X$ is a left-c.e. 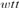$wtt$-complete real having effective Hausdorff dimension 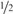${1 / 2}$.

We further investigate the algorithmic properties of 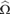${\rm{\hat{\Omega }}}$. For example, we show that the maximal value of 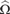${\rm{\hat{\Omega }}}$ must be random, the minimal value must be Turing complete, and that 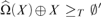${\rm{\hat{\Omega }}}\left( X \right) \oplus X{ \ge _T}\emptyset \prime$ for every X. We also obtain some machine-dependent results, including that for every 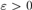$\varepsilon > 0$, there is a universal machine V such that 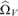${{\rm{\hat{\Omega }}}_V}$ maps every real X having effective Hausdorff dimension greater than ε to a real of effective Hausdorff dimension 0 with the property that 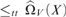$X{ \le _{tt}}{{\rm{\hat{\Omega }}}_V}\left( X \right)$; and that there is a real X and a universal machine V such that ${{\rm{\Omega }}_V}\left( X \right)$ is rational.