Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T21:47:40.736Z Has data issue: false hasContentIssue false
  • English
  • Français

Cauchy completeness in elementary logic

Published online by Cambridge University Press:  12 March 2014

J. C. Cifuentes ,
A. M. Sette  and
D. Mundici
J. C. Cifuentes
Affiliation:
Department of Mathematics, University of Campinas, Caixa Postal 6065, 13081-970 Campinas, SP, Brazil
A. M. Sette
Affiliation:
Department of Mathematics, University of Campinas, Caixa Postal 6065, 13081-970 Campinas, SP, Brazil
D. Mundici
Affiliation:
Department of Computer Science, University of Milan, Via Comelico 39-41, 20135 Milan, Italy, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The inverse of the distance between two structures 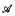≢ 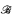of finite type τ is naturally measured by the smallest integer q such that a sentence of quantifier rank q − 1 is satisfied by 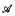but not by 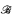. In this way the space Strτ of structures of type τ is equipped with a pseudometric. The induced topology coincides with the elementary topology of Strτ. Using the rudiments of the theory of uniform spaces, in this elementary note we prove the convergence of every Cauchy net of structures, for any type τ.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 61 , Issue 4 , December 1996 , pp. 1153 - 1157
Copyright
Copyright © Association for Symbolic Logic 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bell, J. L. and Slomson, A. B., Models and ultraproducts: An introduction, North-Holland, 1969.Google Scholar
[2]Caicedo, X., Compactness and normality in abstract logics, Annals of Pure and Applied Logic, vol. 59 (1993), pp. 33–43.CrossRefGoogle Scholar
[3]Chang, C. C. and Keisler, H. J., Continuous model theory, Princeton University Press, Princeton, 1966.CrossRefGoogle Scholar
[4]Fraïssé, R., Course de logique mathématique, tome 1, Gauthier-Villars, Paris, 1967.Google Scholar
[5]Frayne, T., Morel, A. C., and Scott, D. S., Reduced direct products, Fundamenta Mathematicae, vol. 51 (1962), pp. 195–228.CrossRefGoogle Scholar
[6]Karp, C., Finite-quantifier equivalence, The theory of models (Addison, , Henkin, , and Tarski, , editors), North-Holland, Amsterdam, 1965.Google Scholar
[7]Kelley, J. L., General topology, D. Van Nostrand, Princeton, 1955.Google Scholar
[8]Kochen, S., Ultraproducts in the theory of models, Annals of Mathematics, vol. 74 (1961), pp. 221–261.CrossRefGoogle Scholar
[9]Mundici, D., Inverse topological systems and compactness in abstract model theory, this Journal, vol. 51 (1986), pp. 785–794.Google Scholar
[10]Tarski, A., Some notions and methods on the borderline of algebra and metamathematics, Proceedings of the International Congress of Mathematics 1950, American Mathematical Society, 1952, pp. 705–720.Google Scholar