Hostname: page-component-cc8bf7c57-n7pht Total loading time: 0 Render date: 2024-12-11T22:55:45.874Z Has data issue: false hasContentIssue false
  • English
  • Français

Cardinalities in the projective hierarchy

Published online by Cambridge University Press:  12 March 2014

Greg Hjorth
Greg Hjorth*
Affiliation:
Department of Mathematics, University of California, Los Angeles, CA 90095-1555, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

We show that the “effective cardinality” of the collection of 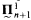sets is strictly bigger than the effective cardinality of the 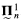. The phrase effective cardinality is vague but can be made exact in the usual ways. For instance:

Theorem 1.1. Assume ADL(ℝ)Then in L(ℝ) there is no injection

.

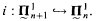A few years ago Tony Martin showed a similar result, establishing the non-existence of an injection from 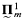to 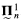for m sufficiently larger than n. His method did not seem to work for m = n + 1.

This present paper gives level by level calculations for the projective hierarchy, but it too falls short of a complete analysis, in as much as it leaves the position of the effective cardinals in the Wadge degrees largely obscure. At the low levels it takes some time for any new cardinals to appear. Whenever Γ1, Γ2 are non-trivial Wadge degrees strictly included in 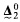one has

.

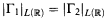Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 4 , December 2002 , pp. 1351 - 1372
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Andretta, A., Notes on descriptive set theory, unpublished manuscript, University of Turino, 2000.Google Scholar
[2]Hjorth, G., A dichotomy for the definable universe, this Journal, vol. 60 (1995), pp. 1199–1207.Google Scholar
[3]Hjorth, G., An absoluteness principle for Borel sets, this Journal, vol. 63 (1998), pp. 663–693.Google Scholar
[4]Hjorth, G., Classification and orbit equivalence relations, American Mathematical Society Mathematical Surveys and Monographs Series, Rhode Island, 2000.Google Scholar
[5]Martin, D. A., Moschovakis, Y. N., and Steel, J. R., The extent of definable scales, Bulletin of the American Mathematical Society, vol. 6 (1982), pp. 435–440.CrossRefGoogle Scholar
[6]Martin, D. A. and Steel, J. R., The extent of scales in L(ℝ), Cabal Seminar 79–81 (Kechris, A. S., Martin, D. A., and Steel, J. R., editors), vol. 1019, pp. 86–96.CrossRefGoogle Scholar
[7]Moschovakis, Y. N., Descriptive Set Theory, North-Holland, Amsterdam, 1980.Google Scholar