No CrossRef data available.
Article contents
CANTORIAN MODELS OF PREDICATIVE 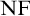 $\mathrm {NF}$
$\mathrm {NF}$
Published online by Cambridge University Press: 13 October 2022
Abstract
Tangled Type Theory was introduced by Randall Holmes in [3] as a new way of approaching the consistency problem for 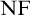 $\mathrm {NF}$. Although the task of finding models for this theory is far from trivial (considering it is equiconsistent with
$\mathrm {NF}$. Although the task of finding models for this theory is far from trivial (considering it is equiconsistent with 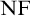 $\mathrm {NF}$), ways of constructing models for certain fragments of it have been discovered. In this article, we present a simpler way of constructing models of predicative Tangled Type Theory and consequently of predicative
$\mathrm {NF}$), ways of constructing models for certain fragments of it have been discovered. In this article, we present a simpler way of constructing models of predicative Tangled Type Theory and consequently of predicative 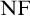 $\mathrm {NF}$. In these new models of predicative
$\mathrm {NF}$. In these new models of predicative 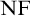 $\mathrm {NF}$, the universe is well-orderable and equinumerous to the set of singletons.
$\mathrm {NF}$, the universe is well-orderable and equinumerous to the set of singletons.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic



