Article contents
Bounds for the closure ordinals of essentially monotonic increasing functions
Published online by Cambridge University Press: 12 March 2014
Abstract
Let Ω ≔ ℵ1. For any α< εΩ + 1 ≔ min {ξ > Ω: ξ = ωξ} let EΩ(α) be the finite set of ε-numbers below Ω which are needed for the unique representation of α in Cantor-normal form using 0, Ω, +, and ω. Let α* ≔ max(EΩ(α) ∪ {0}). A function f: εΩ + 1 → Ω is called essentially increasing, if for any α < εΩ + 1; f(α) ≥ α*: f is called essentially monotonic, if for any α, β<εΩ + 1;
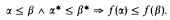
Let 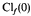 be the least set of ordinals which contains 0 as an element and which satisfies the following two conditions:
be the least set of ordinals which contains 0 as an element and which satisfies the following two conditions:
(a)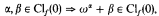
(b)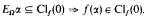
Let 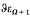 be the Howard-Bachmann ordinal, which is, for example, defined in [3]. The following theorem is shown: If f: εΩ + 1 → Ω is essentially monotonic and essentially increasing, then the order type of
be the Howard-Bachmann ordinal, which is, for example, defined in [3]. The following theorem is shown: If f: εΩ + 1 → Ω is essentially monotonic and essentially increasing, then the order type of 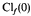 is less than or equal to
is less than or equal to 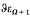 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1993
References
REFERENCES
- 3
- Cited by


