Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T20:20:56.986Z Has data issue: false hasContentIssue false
  • English
  • Français

THE BOREL COMPLEXITY OF ISOMORPHISM FOR O-MINIMAL THEORIES

Published online by Cambridge University Press:  19 June 2017

RICHARD RAST  and
DAVENDER SINGH SAHOTA
RICHARD RAST
Affiliation:
UNIVERSITY OF MARYLAND COLLEGE PARK, MD, USAE-mail: [email protected]
DAVENDER SINGH SAHOTA
Affiliation:
UNIVERSITY OF ILLINOIS AT CHICAGO CHICAGO, IL, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a countable o-minimal theory T, we characterize the Borel complexity of isomorphism for countable models of T up to two model-theoretic invariants. If T admits a nonsimple type, then it is shown to be Borel complete by embedding the isomorphism problem for linear orders into the isomorphism problem for models of T. This is done by constructing models with specific linear orders in the tail of the Archimedean ladder of a suitable nonsimple type.

If the theory admits no nonsimple types, then we use Mayer’s characterization of isomorphism for such theories to compute invariants for countable models. If the theory is small, then the invariant is real-valued, and therefore its isomorphism relation is smooth. If not, the invariant corresponds to a countable set of reals, and therefore the isomorphism relation is Borel equivalent to F2.

Combining these two results, we conclude that 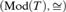$\left( {{\rm{Mod}}\left( T \right), \cong } \right)$ is either maximally complicated or maximally uncomplicated (subject to completely general model-theoretic lower bounds based on the number of types and the number of countable models).

Keywords

03C64Borel complexity of isomorphismO-minimalBorel complete
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 2 , June 2017 , pp. 453 - 473
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Friedman, H. and Stanley, L., A Borel reducibility theory for classes of countable structures, this Journal, vol. 54 (1989), pp. 894–914.Google Scholar
Kechris, A., Classical Descriptive Set Theory, first ed., Graduate Texts in Mathematics, Springer , New York, 1995.CrossRefGoogle Scholar
Knight, J., Pillay, A., and Steinhorn, C., Definable sets in ordered structures. II . Transactions of the American Mathematical Society, vol. 295 (1986), pp. 593–605.CrossRefGoogle Scholar
Marker, D., Omitting types in o-minimal theories , this Journal, vol. 51 (1986), pp. 63–74.Google Scholar
Marker, D., Model Theory: An Introduction, Graduate Texts in Mathematics, vol. 217, Springer, New York, 2002.Google Scholar
Marker, D., The Borel complexity of isomorphism for theories with many types . Notre Dame Journal of Formal Logic, vol. 48 (2007),no. 1, pp. 93–97.CrossRefGoogle Scholar
Mayer, L. L., Vaught’s conjecture for o-minimal theories , this Journal, vol. 53 (1988), pp. 146–159.Google Scholar
Pillay, A. and Steinhorn, C., Definable sets in ordered structures . I. Transactions of the American Mathematical Society, vol. 295 (1986), pp. 565–592.CrossRefGoogle Scholar
Pillay, A. and Steinhorn, C., Discrete o-minimal structures .Annals of Pure and Applied Logic, vol. 34 (1987), pp. 275–289.CrossRefGoogle Scholar
Singh Sahota, D., Borel complexity of the isomorphism relation for O-minimal theories. Ph.D. thesis, University of Illinois at Chicago, 2013.Google Scholar