No CrossRef data available.
Article contents
Boolean combinations of r.e. open sets
Published online by Cambridge University Press: 12 March 2014
Extract
In [2], [3], J. Grassin characterized those classes of sets which are expressible as a Boolean combination of open sets in the Baire topology on the power set of the natural numbers. From this characterization he deduced that if 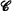 is a Boolean combination of recursive open sets, then the minimum length for any Boolean combination representing
is a Boolean combination of recursive open sets, then the minimum length for any Boolean combination representing 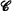 can be realized using recursive open sets.
can be realized using recursive open sets.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1976
References
REFERENCES
[1]
Ershov, Y. L., A hierarchy of sets. I, Algebra and Logic, vol. 7 (1968), pp. 25–43.CrossRefGoogle Scholar
[2]
Grassin, J., Ensembles d'indices des combinaisons booléennes d'ouverts dont une clé est recursivement énumérable, Thesis, Université d'Orléans, 1972.Google Scholar
[3]
Grassin, J., Index sets in Ershov's hierarchy, this Journal, vol. 39 (1974), pp. 97–104.Google Scholar
[5]
Rogers, H. Jr., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar


