Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T13:53:57.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Bisimulations and predicate logic

Published online by Cambridge University Press:  12 March 2014

Tim Fernando
Tim Fernando*
Affiliation:
Institut für Maschinelle Sprachverarbeitung, University of Stuttgart, D 70174 Stuttgart, Germany, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Elementary (first-order) and nonelementary (set-theoretic) aspects of the largest bisimulation are considered with a view toward analyzing operational semantics from the perspective of predicate logic. The notion of a bisimulation is employed in two distinct ways: (i) as an extensional notion of equivalence on programs (or processes) generalizing input/output equivalence (at a cost exceeding 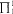over certain transition predicates computable in log space), and (ii) as a tool for analyzing the dependence of transitions on data (which can be shown to be elementary or nonelementary, depending on the formulation of the transitions).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 3 , September 1994 , pp. 924 - 944
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abramsky, Samson, A domain equation for bisimulation, Information and Computation, vol. 92 (1991), pp. 161–218.CrossRefGoogle Scholar
[2]Aceto, L., Bloom, B., and Vaandrager, F., Turning SOS rules into equations, Proceedings, seventh annual symposium on logic in computer science, IEEE Computer Society Press, Washington, D.C., 1992.Google Scholar
[3]Aczel, Peter, An introduction to inductive definitions, Handbook of Mathematical Logic (Barwise, J., editor), North-Holland, Amsterdam, 1977.Google Scholar
[4]Aczel, Peter, Non-well-founded sets, Center for the Study of Language and Information, Lecture Notes, no. 14, Stanford, California, 1988.Google Scholar
[5]Baeten, J. C. M. and Weijland, W.P., Process algebra, Cambridge Tracts in Theoretical Computer Science, vol. 18, Cambridge University Press, London and New York, 1990.CrossRefGoogle Scholar
[6]Barwise, J., Gandy, R. O., and Moschovakis, Y. N., The next admissible set, this Journal, vol. 36 (1971), pp. 108–120.Google Scholar
[7]Barwise, Jon, Admissible sets and structures, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1975.CrossRefGoogle Scholar
[8]van Benthem, J. and Bergstra, J., Logic of transition systems, Technical report, Institute for Logic, Language and Information, Amsterdam, 03 1993.Google Scholar
[9]van Benthem, Johan, Modal logic and classical logic, Bibliopolis, Napoli, 1985.Google Scholar
[10]van Benthem, Johan, Language in action: Categories, lambdas and dynamic logic, North-Holland, Amsterdam, 1991.Google Scholar
[11]van Benthem, Johan, Which program constructions are safe for bisimulation?, Technical report, Institute for Logic, Language and Information, Amsterdam, 02 1993.Google Scholar
[12]Bloom, B., Istrail, S., and Meyer, A. R., Bisimulation can’t be traced, Journal of the Association for Computing Machinery (1988).Google Scholar
[13]Christensen, S., Hirshfield, Y., and Moller, F., Decomposability, decidability, and axiomatisability for bisimulation equivalence on basic parallel processes, Proceedings, eighth annual symposium on logic in computer science, IEEE Computer Society Press, Washington, DC., 1993.Google Scholar
[14]Darondeau, Ph. and Yoccoz, S., Proof systems for infinite behaviours, Information and computation,, vol. 99 (1992).Google Scholar
[15]Darondeau, Philippe, Concurrency and computability, Semantics of systems of concurrentprocesses (Guessarian, I., editor), Lecture Notes in Computer Science, vol. 469, Springer-Verlag, Berlin, 1990.Google Scholar
[16]Feferman, Solomon and Spector, Clifford, Incompleteness along paths in progressions of theories, this Journal, vol. 27 (1962).Google Scholar
[17]Fernando, Tim, Transition systems and dynamic semantics, Logics in AI (Pearce, D. and Wagner, G., editors), Lecture Notes in Computer Science, vol. 633 (subseries Lecture Notes in Artifical Intelligence), Springer-Verlag, Berlin, 1992: a slightly corrected version has appeared as CWI ReportCS-R9217, June 1992.CrossRefGoogle Scholar
[18]Fernando, Tim, Comparative transition system semantics, Computer science logic: Selected papers from CSL ’92, (Börger, E.et al., editors), Lecture Notes in Computer Science, vol. 702, Springer-Verlag, Berlin, 1993.CrossRefGoogle Scholar
[19]Fernando, Tim, A path from generalized recursion back to mechanical computation, manuscript for a talk given at a meeting on ‘Proofs and Computation’, Oslo, 09 1993.Google Scholar
[20]Friedman, Harvey, Recursiveness in paths through &, Proceedings of the American Mathematical Society, vol. 54 (1976), pp. 311–315.Google Scholar
[21]Gandy, Robin O., Proof of Mostowski's conjecture, Bulletin of the Polish Academy of Science, vol. 8 (1960).Google Scholar
[22]Grigorieff, Serge, Every recursive linear ordering has a copy in DTIME-SPACE(n. log(n)), this Journal, vol. 55 (1990), pp. 571–575.Google Scholar
[23]Harel, David, Dynamic logic, Handbook of philosophical logic (Gabbay, D. and Guenther, F., editors), vol. 2, D. Reidel, Dordrecht, 1984.Google Scholar
[24]Hennessy, M. and Milner, R., Algebraic laws for nondeterminism and concurrency, Journal of the Association for Computing Machinery, vol. 32 (1985).CrossRefGoogle Scholar
[25]Keisler, H. Jerome, Forcing and the omitting types theorem, Studies in model theory (Morley, M., editor), The Mathematical Association of America, Washington, DC., 1973.Google Scholar
[26]Keisler, H. Jerome, Fundamentals of model theory, Handbook of mathematical logic (Barwise, J., editor), North-Holland, Amsterdam, 1977.Google Scholar
[27]Klop, Jan Willem, Lectures on bisimulation semantics: the material on ‘ordinal processes’ (cited above) appeared in course notes for lectures given at the REX workshop, Noordwijkerhout, May 1988, but regretably not in the proceedings of the workshop (Lecture Notes in Computer Sciences, vol. 354).Google Scholar
[28]Milner, Robin, Communication and concurrency, Prentice Hall, Englewood Cliffs, New Jersey, 1989.Google Scholar
[29]Park, David, Concurrency and automata on infinite sequences, Proceedings of the 5th GI Conference (Deussen, P., editor), Lecture Notes in Computer Science, vol. 104, Springer-Verlag, Berlin, 1981, pp. 167–183.Google Scholar
[30]Plotkin, Gordon D.. A structural approach to operational semantics, Technical Report DAIMIFN-19, Computer Science Department, Aarhus University, 1981.Google Scholar
[31]Stirling, Colin, Modal and temporal logics, Handbook of logic in computer science (Gabbay, D. M., Abramsky, S., and Maibaum, T. S. E., editors), vol. 2, Clarendon Press, Oxford, 1992.Google Scholar
[32]Vaandrager, Frits W., Expressiveness results for process algebras, Proceedings of the REX Workshop (de Bakker, J. W.et al., editors), Lecture Notes in Computer Science, vol. 666, Springer-Verlag, Berlin, 1993: also appears as CWI Technical Report CS-R9301, Amsterdam, 01 1993.Google Scholar