Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-25T17:03:06.002Z Has data issue: false hasContentIssue false
  • English
  • Français

BI-INTERPRETATION IN WEAK SET THEORIES

Published online by Cambridge University Press:  30 October 2020

ALFREDO ROQUE FREIRE  and
JOEL DAVID HAMKINS
ALFREDO ROQUE FREIRE
Affiliation:
PHILOSOPHY DEPARTMENT UNIVERSITY OF BRASÍLIA BRASÍLIA, BRAZILE-mail:[email protected]: http://alfredoroquefreire.com
JOEL DAVID HAMKINS
Affiliation:
SIR PETER STRAWSON FELLOW IN PHILOSOPHY UNIVERSITY COLLEGE, OXFORD PROFESSOR OF LOGIC, FACULTY OF PHILOSOPHY UNIVERSITY OF OXFORD AFFILIATE MEMBER DEPARTMENT OF MATHEMATICS, UNIVERSITY OF OXFORDOXFORD, UKE-mail:[email protected]: http://jdh.hamkins.org
Get access Rights & Permissions [Opens in a new window]

Abstract

In contrast to the robust mutual interpretability phenomenon in set theory, Ali Enayat proved that bi-interpretation is absent: distinct theories extending ZF are never bi-interpretable and models of ZF are bi-interpretable only when they are isomorphic. Nevertheless, for natural weaker set theories, we prove, including Zermelo–Fraenkel set theory $\mathrm {ZFC}^{-}$ without power set and Zermelo set theory Z, there are nontrivial instances of bi-interpretation. 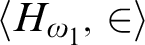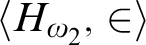Specifically, there are well-founded models of $\mathrm {ZFC}^{-}$ that are bi-interpretable, but not isomorphic—even $\langle H_{\omega _1},\in \rangle $ and $ \langle H_{\omega _2},\in \rangle $ can be bi-interpretable—and there are distinct bi-interpretable theories extending $\mathrm {ZFC}^{-}$ . Similarly, using a construction of Mathias, we prove that every model of ZF is bi-interpretable with a model of Zermelo set theory in which the replacement axiom fails.

Keywords

model theory of set theorybi-interpretationmutual interpretationtightness
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 2 , June 2021 , pp. 609 - 634
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Commentary can be made about this article on the second author’s blog at http://jdh.hamkins.org/bi-interpretation-in-weak-set-theories.

References

Apter, A. W., Gitman, V., and Hamkins, J. D., Innermodels with large cardinal features usually obtained by forcing. Archive for Mathematical Logic, vol. 51 (2012), no. 3, pp. 257–283.CrossRefGoogle Scholar
de Bouvère, K. L., Logical synonymy. Indagationes Mathematicae, vol. 27 (1965), pp. 622–629.CrossRefGoogle Scholar
Enayat, A., Variations on a Visserian theme, Liber Amicorum Alberti: A Tribute to Albert Visser (van Eijck, J., Iemhoff, R., and Joosten, J. J., editors), College Publications, London, 2016, pp. 99–110.Google Scholar
Freire, A. R., On what counts as a translation, The Logica Yearbook 2007 (Peliš, M., editor), Filosofia, Prague, Czech Republic, 2008.Google Scholar
Freire, A. R., Estudo comparado do comprometimento ontológico das teorias de classes e conjuntos, Ph.D. thesis, University of Campinas, 2019.Google Scholar
Freire, A. R. and de Alvarenga Freire, R., The ontological import of adding proper classes. Manuscrito, vol. 42 (2019), no. 2, pp. 85–112.CrossRefGoogle Scholar
Friedman, H. M. and Visser, A., When bi-interpretability implies synonymy. Logic Group Preprint Series, vol. 320 (2014), pp. 1–19.Google Scholar
Fuchs, G., Hamkins, J. D., and Reitz, J., Set-theoretic geology. Annals of Pure and Applied Logic, vol. 166 (2015), no. 4, pp. 464–501.CrossRefGoogle Scholar
Gitman, V. and Hamkins, J. D., A natural model of the multiverse axioms. Notre Dame Journal of Formal Logic, vol. 51 (2010), no. 4, pp. 475–484.CrossRefGoogle Scholar
Gitman, V., Hamkins, J. D., and Johnstone, T. A., What is the theory ZFC without powerset? Mathematical Logic Quarterly, vol. 62 (2016), no. 4–5, pp. 391–406.CrossRefGoogle Scholar
Goldberg, G., Can ${H}_{\omega_1}$ and ${H}_{\omega_2}$ be in bi-interpretation synonymy? MathOverflow answer, 2020. Available at https://mathoverflow.net/q/350585 (accessed 16 January, 2020).Google Scholar
Hamkins, J. D., The set-theoretic multiverse. Review of Symbolic Logic, vol. 5 (2012), no. 3, pp. 416–449.CrossRefGoogle Scholar
Hamkins, J. D., Different set theories are never bi-interpretable. Mathematics and Philosophy of the Infinite, 2018. Available at http://jdh.hamkins.org/different-set-theories-are-never-bi-interpretable/ (accessed 27 March, 2018).Google Scholar
Hamkins, J. D., Can ${H}_{\omega_1}$ and ${H}_{\omega_2}$ be in bi-interpretation synonymy? MathOverflow question, 2020. Available at https://mathoverow.net/q/350542 (accessed 16 January, 2020).Google Scholar
Hamkins, J. D., The real numbers are not interpretable in the complex field. Mathematics and Philosophy of the Infinite, 2020. Available at http://jdh.hamkins.org/the-real-numbers-are-not-interpretable-in-thecomplex-field/ (accessed 24 February, 2020).Google Scholar
Harrington, L., Long projective wellorderings. Annals of Mathematical Logic, vol. 12 (1977), no. 1, pp. 1–24.CrossRefGoogle Scholar
Hodges, W., Model Theory , Encyclopedia of Mathematics and Its Applications , vol. 42, Cambridge University Press, Cambridge, 1993.Google Scholar
Hamkins, J. D. and Seabold, D., Well-founded Boolean ultrapowers as large cardinal embeddings, Mathematics and Philosophy of the Infinite, 2006, pp. 1–40. arXiv:1206.6075[math.LO]. Available at http://jdh.hamkins.org/boolean-ultrapowers/ Google Scholar
Laver, R., Certain very large cardinals are not created in small forcing extensions. Annals of Pure and Applied Logic. Vol. 149 (2007), no. 1, pp. 1–6.CrossRefGoogle Scholar
Mathias, A. R. D., Slim models of Zermelo set theory, this Journal, vol. 66 (2001), no. 2, pp. 487–496.Google Scholar
Schlipf, J. S., Toward model theory through recursive saturation, this Journal, vol. 43 (1978), no. 2, pp. 183–206.Google Scholar
Visser, A., Categories of theories and interpretations, Logic in Tehran, Lecture Notes in Logic, vol. 26, Association for Symbolic Logic, La Jolla, CA, 2006, pp. 284–341.CrossRefGoogle Scholar
Väänänen, J., An extension of a theorem of Zermelo. The Bulletin of Symbolic Logic, vol. 25 (2019), no. 2, 208–212.CrossRefGoogle Scholar