Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T22:22:36.138Z Has data issue: false hasContentIssue false
  • English
  • Français

The Bass-Milnor-Serre theorem for nonstandard models in Peano arithmetic

Published online by Cambridge University Press:  12 March 2014

Anatole Khelif
Anatole Khelif*
Affiliation:
Equipe de Logique Mathématique, Université Paris-VII, 75251 Paris, France, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The aim of this paper is to extend the Bass-Milnor-Serre theorem to the nonstandard rings associated with nonstandard models of Peano arithmetic, in brief to Peano rings.

First, we recall the classical setting. Let k be an algebraïc number field, and let θ be its ring of integers. Let n be an integer ≥ 3, and let G be the group Sln(θ) of (n, n) matrices of determinant 1 with coefficients in θ.

The profinite topology in G is the topology having as fundamental system of open subgroups the subgroups of finite index.

Congruence subgroups of finite index of G are the kernels of the maps Sln(θ) → Sln(θ/I) for which all ideals I of θ are of finite index. By taking these subgroups as a fundamental system of open subgroups, one obtains the congruence topology on G. Every open set for this topology is open in the profinite topology.

We denote by Ḡ (resp., Ĝ) the completion of G for the congruence (resp., profinite) topology.

The Bass-Milnor-Serre theorem [1] consists of the two following statements:

(A) If k admits a real embedding, then we have an exact sequence

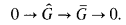
That is, Ĝ and Ḡ are isomorphic.

(B) If k is totally imaginary, then one has an exact sequence

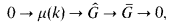
where μ(k)is the group of the roots of unity of k.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 4 , December 1993 , pp. 1451 - 1458
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bass, H., Milnor, J., and Serre, J. P., Solution of the congruence subgroup problem for SLn (n ≥ 3) and Sp2n (n ≥ 2), Institut des Hautes Études Scientifiques Publícations Mathématiques, vol. 33 (1967), pp. 59–137.CrossRefGoogle Scholar
[2]Selberg, Atle, An elementary proof of Dirichlet's theorem about primes, Annals of Mathematics, vol. 50(1949), pp. 297–304.CrossRefGoogle Scholar
[3]Lang, S., Algebraic number theory, Addison-Wesley Publishing Company, Menlo Park, California, 1970.Google Scholar
[4]Carter, D. and Keller, Gordon, Elementary generation of SLn(θ), American Journal of Mathematics, vol. 105 (1983), pp. 673–686.CrossRefGoogle Scholar
[5]Macintyre, Angus, Residue fields of models of P, Logic, methodology and philosophy of science VI (Hannover 1979), North-Holland Publishing Company and PWN-Polish Scientific Publishers, 1982, pp. 193–206.Google Scholar
[6]Ax, J., The elementary theory of finite fields, Annals of Mathematics, vol. 2 (1968), pp. 239–271.CrossRefGoogle Scholar
[7]Khelif, Anatole, Dirichlet's theorem about primes in nonstandard models of Peano, in preparation.Google Scholar