Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-14T14:08:15.378Z Has data issue: false hasContentIssue false
  • English
  • Français

BASES AND BOREL SELECTORS FOR TALL FAMILIES

Published online by Cambridge University Press:  30 January 2019

JAN GREBÍK  and
CARLOS UZCÁTEGUI
JAN GREBÍK
Affiliation:
INSTITUTE OF MATHEMATICS ACADEMY OF SCIENCES OF THE CZECH REPUBLIC ŽITNÁ 609/25, 110 00PRAHA 1-NOVÉ MĚSTO CZECH REPUBLIC E-mail: [email protected]
CARLOS UZCÁTEGUI
Affiliation:
ESCUELA DE MATEMÁTICAS UNIVERSIDAD INDUSTRIAL DE SANTANDER CRA. 27 CALLE 9 UIS EDIFICIO 45 BUCARAMANGA, COLOMBIAE-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a family ${\cal C}$ of infinite subsets of ${\Bbb N}$, we study when there is a Borel function 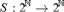$S:2^{\Bbb N} \to 2^{\Bbb N} $ such that for every infinite 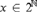$x \in 2^{\Bbb N} $, 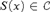$S\left( x \right) \in {\Cal C}$ and 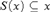$S\left( x \right) \subseteq x$. We show that the family of homogeneous sets (with respect to a partition of a front) as given by the Nash-Williams’ theorem admits such a Borel selector. However, we also show that the analogous result for Galvin’s lemma is not true by proving that there is an 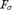$F_\sigma $ tall ideal on ${\Bbb N}$ without a Borel selector. The proof is not constructive since it is based on complexity considerations. We construct a 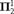${\bf{\Pi }}_2^1 $ tall ideal on ${\Bbb N}$ without a tall closed subset.

Keywords

Primary 03E1503E05Borel idealstall familiesBorel selectorGalvin’s Lemma
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 1 , March 2019 , pp. 359 - 375
Copyright
Copyright © The Association for Symbolic Logic 2019 

References

REFERENCES

Avigad, J., An effective proof that open sets are Ramsey. Archive for Mathematical Logic, vol. 37 (1998), no. 4, pp. 235–240.10.1007/s001530050095CrossRefGoogle Scholar
Becker, H., Kahane, S., and Louveau, A., Some complete ${\text{\Sigma }}_2^1 $ sets in harmonic analysis. Transactions of the American Mathematical Society, vol. 339 (1993), no. 1, pp. 323–336.Google Scholar
Galvin, F. and Prikry, K., Borel sets and Ramsey’s theorem, this Journal, vol. 38 (1973), pp. 193–198.Google Scholar
Gao, S., Invariant Descriptive Set Theory, Pure and Applied Mathematics, vol. 293, CRC Press, Boca Raton, FL, 2009.Google Scholar
Grebík, J. and Hrušák, M., No minimal tall Borel ideal in the Katětov order, 2017, arxiv.org/pdf/1708.05322.pdf.Google Scholar
Hrušák, M., Katětov order on Borel ideals. Archive for Mathematical Logic, vol. 56 (2017), no. 7–8, pp. 831–847.10.1007/s00153-017-0543-xCrossRefGoogle Scholar
Hrus̆ák, M., Meza-Alcántara, D., Thümmel, E., and Uzcátegui, C., Ramsey type properties of ideals. Annals of Pure and Applied Logic, vol. 168 (2017), no. 11, pp. 2022–2049.10.1016/j.apal.2017.06.001CrossRefGoogle Scholar
Kechris, A. S., Classical Descriptive Set Theory, Springer-Verlag, New York, 1994.Google Scholar
Mathias, A. R. D., Happy families. Archive for Mathematical Logic, vol. 12 (1977), pp. 11–59.Google Scholar
Mazur, K., $F_\sigma $ -ideals and $\omega _1 \omega _1^{\text{*}} $ -gaps in the Boolean algebras$P\left( \omega \right)/I$ . Fundamenta Mathematicae, vol. 138 (1991), no. 2, pp. 103–111.10.4064/fm-138-2-103-111CrossRefGoogle Scholar
St, C.. Nash-Williams, J. A., On better-quasi-ordering transfinite sequences. Mathematical Proceedings of the Cambridge Philosophical Society, vol. 64 (1968), no. 2, pp. 273–290.Google Scholar
Silver, J., Every analytic set is Ramsey, this Journal, vol. 35 (1970), pp. 60–64.Google Scholar
Solecki, S., Filters and sequences. Fundamenta Mathematicae, vol. 163 (2000), no. 3, pp. 215–228.Google Scholar
Solovay, R., Hyperarithmetically encodable sets. Transactions of the American Mathematical Society, vol. 239 (1978), pp. 99–122.10.1090/S0002-9947-1978-0491103-7CrossRefGoogle Scholar
Todorčević, S., Higher dimensional Ramsey theory, Ramsey Methods in Analysis (Argyros, S. and Todorčević, S., editors), Advanced Courses in Mathematics, CRM Barcelona, Birkhäuser, Basel, 2005.Google Scholar
Todorčević, S., Introduction to Ramsey Spaces. Annals of Mathematical Studies, vol. 174. Princeton University Press, Princeton, NJ, 2010.Google Scholar