Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T19:21:09.149Z Has data issue: false hasContentIssue false
  • English
  • Français

AXIOM I0 AND HIGHER DEGREE THEORY

Published online by Cambridge University Press:  22 July 2015

XIANGHUI SHI
XIANGHUI SHI*
Affiliation:
SCHOOL OF MATHEMATICAL SCIENCES BEIJING NORMAL UNIVERSITY KEY LABORATORY OF MATHEMATICS AND COMPLEX SYSTEMS MINISTRY OF EDUCATION BEIJING 100875 P.R. CHINAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we analyze structures of Zermelo degrees via a list of four degree theoretic questions (see §2) in various fine structure extender models, or under large cardinal assumptions. In particular we give a detailed analysis of the structures of Zermelo degrees in the Mitchell model for ω many measurable cardinals. It turns out that there is a profound correlation between the complexity of the degree structures at countable cofinality singular cardinals and the large cardinal strength of the relevant cardinals. The analysis applies to general degree notions, Zermelo degree is merely the author’s choice for illustrating the idea.

I0(λ) is the assertion that there is an elementary embedding j : L(Vλ+1) → L(Vλ+1) with critical point < λ. We show that under I0(λ), the structure of Zermelo degrees at λ is very complicated: it has incomparable degrees, is not dense, satisfies Posner–Robinson theorem etc. In addition, we show that I0 together with a mild condition on the critical point of the embedding implies that the degree determinacy for Zermelo degrees at λ is false in L(Vλ+1). The key tool in this paper is a generic absoluteness theorem in the theory of I0, from which we obtain an analogue of Perfect Set Theorem for “projective” subsets of Vλ+1, and the Posner–Robinson follows as a corollary. Perfect Set Theorem and Posner–Robinson provide evidences supporting the analogy between 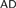$$AD$$ over L(ℝ) and I0 over L(Vλ+1), while the failure of degree determinacy is one for disanalogy. Furthermore, we conjecture that the failure of degree determinacy for Zermelo degrees at any uncountable cardinal is a theorem of 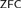$$ZFC$$.

Keywords

Axiom I0Prikry type forcinggeneric absolutenessλ-Perfect Set TheoremPosner–Robinson Theoremdegree determinacyindestructibly supercompacthigher degree theoryCovering Lemma
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 3 , September 2015 , pp. 970 - 1021
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abraham, Uri, Proper forcing, Handbook of set theory. Springer, Dordrecht, 2010, pp. 333–394.CrossRefGoogle Scholar
Becker, Howard, Inner model operators and the continuum hypothesis. Proceedings of the American Mathematical Society, vol. 96 (1986), no. 1, pp. 126–129.CrossRefGoogle Scholar
Cramer, Scott Stefan, Inverse limit reflection and the structure of L(V λ+1), Ph.D. thesis, University of California, Berkeley, 2012.Google Scholar
Devlin, Keith J., Constructibility, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1984.CrossRefGoogle Scholar
Dimonte, Vincenzo and Friedman, Sy-David, Rank-into-rank hypotheses and the failure of GCH, Archive for Mathematical Logic, vol. 53 (2014), no. 3-4, pp. 351–366.Google Scholar
Dodd, A. J. and Jensen, R. B., The covering lemma for L[U]. Annals of Mathematical Logic, vol. 22 (1982), no. 2, pp. 127–135.Google Scholar
Dodd, Tony and Jensen, Ronald, The covering lemma for K. Annals of Mathematical Logic, vol. 22 (1982), no. 1, pp. 1–30.Google Scholar
Friedman, Sy D., Negative solutions to Post’s problem. I, Generalized recursion theory, II (Proceedings of Second Symposium, University of Oslo, Oslo, 1977), Studies in Logic and the Foundations of Mathematics, vol. 94, North-Holland, Amsterdam, 1978, pp. 127–133.CrossRefGoogle Scholar
Friedman, Sy D., Negative solutions to Post’s problem. II. Annals of Mathematical Logic, vol. 113 (1981), no. 1, pp. 25–43.Google Scholar
Gaifman, Haim, Elementary embeddings of models of set-theory and certain subtheories, Axiomatic set theory (Proceedings of Symposia in Pure Mathematics, Vol. XIII, Part II, Univesity of California, Los Angeles, California, 1967), American Mathematical Society, Providence R.I., 1974, pp. 33–101.Google Scholar
Gitik, Moti, The negation of the singular cardinal hypothesis from o(κ) = κ ++. Annals of Pure and Applied Logic, vol. 43 (1989), no. 3, pp. 209–234.CrossRefGoogle Scholar
Gitik, Moti, Prikry-type forcings, Handbook of set theory. Springer, Dordrecht, 2010, pp. 1351–1447.CrossRefGoogle Scholar
Hamkins, Joel David, Small forcing makes any cardinal superdestructible, this Journal, vol. 63 (1998), no. 1, pp. 51–58.Google Scholar
Harrison, Joseph, Recursive pseudo-well-orderings. Transactions of the American Mathematical Society, vol. 131 (1968), pp. 526–543.CrossRefGoogle Scholar
Jech, Thomas, Set theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Jensen, Ronald B., Forcing with classes of conditions, Chapter 6 of Admissible Sets, URL: http://www.mathematik.hu-berlin.de/∼raesch/org/jensen/pdf/AS\_6.pdf.Google Scholar
Kanamori, Akihiro, The higher infinite, Second edition, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Kechris, Alexander S., Kleinberg, Eugene M., Moschovakis, Yiannis N., and Woodin, W. Hugh, The axiom of determinacy, strong partition properties and nonsingular measures, Cabal Seminar 77–79 (Proc. Caltech-UCLA Logic Sem., 1977–79), Lecture Notes in Mathematics, vol. 839, Springer, Berlin, 1981, pp. 75–99.Google Scholar
Kleinberg, Eugene M., Infinitary combinatorics and the axiom of determinateness, Lecture Notes in Mathematics, Vol. 612, Springer-Verlag, Berlin, 1977.CrossRefGoogle Scholar
Kunen, Kenneth, Elementary embeddings and infinitary combinatorics, this Journal, vol. 36 (1971), pp. 407–413.Google Scholar
Laver, Richard, Making the supercompactness of κ indestructible under κ-directed closed forcing. Israel Journal of Mathematics, vol. 29 (1978), no. 4, pp. 385–388.CrossRefGoogle Scholar
Laver, Richard, The left distributive law and the freeness of an algebra of elementary embeddings. Advances in Mathematics, vol. 91 (1992), no. 2, pp. 209–231.CrossRefGoogle Scholar
Laver, Richard, A division algorithm for the free left distributive algebra, Logic Colloquium ’90 (Helsinki, 1990), Lecture Notes Logic, vol. 2, Springer, Berlin, 1993, pp. 155–162.Google Scholar
Laver, Richard, On the algebra of elementary embeddings of a rank into itself. Advances in Mathematics, vol. 110 (1995), no. 2, pp. 334–346.CrossRefGoogle Scholar
Laver, Richard, Braid group actions on left distributive structures, and well orderings in the braid groups. Journal of Pure and Applied Algebra, vol. 108 (1996), no. 1, pp. 81–98.CrossRefGoogle Scholar
Laver, Richard, Implications between strong large cardinal axioms. Annals of Pure and Applied Logic, vol. 90 (1997), no. 1–3, pp. 79–90.CrossRefGoogle Scholar
Laver, Richard, Reflection of elementary embedding axioms on the L[V λ+1] hierarchy. Annals of Pure and Applied Logic, vol. 107 (2001), no. 1–3, pp. 227–238.CrossRefGoogle Scholar
Laver, Richard, On very large cardinals, Paul Erdős and his mathematics, II (Budapest, 1999), Bolyai Society Mathematical Studies, vol. 11, János Bolyai Mathematical Society, Budapest, 2002, pp. 453–469.Google Scholar
Mitchell, W. J., On the singular cardinal hypothesis. Transactions of the American Mathematical Society, vol. 329 (1992), no. 2, pp. 507–530.Google Scholar
Mitchell, William J., The covering lemma, Handbook of set theory. Springer, Dordrecht, 2010, pp. 1497–1594.CrossRefGoogle Scholar
Neeman, Itay, Inner models in the region of a Woodin limit of Woodin cardinals. Annals of Pure and Applied Logic, vol. 116 (2002), no. 1–3, pp. 67–155.CrossRefGoogle Scholar
Posner, David B. and Robinson, Robert W., Degrees joining to , this Journal, vol. 46 (1981), no. 4, pp. 714–722.Google Scholar
Sacks, Gerald E., Higher recursion theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1990.CrossRefGoogle Scholar
Sacks, Gerald E. and Slaman, Theodore A., Generalized hyperarithmetic theory. Proceedings of the London Mathematical Society, vol. 60 (1990), no. 3, pp. 417–443.CrossRefGoogle Scholar
Sami, Ramez L., Turing determinacy and the continuum hypothesis. Archive for Mathematical Logic, vol. 28 (1989), no. 3, pp. 149–154.Google Scholar
Sargsyan, Grigor, Descriptive inner model theory. Bulletin of Symbolic Logic, vol. 19 (2013), no. 1, pp. 1–55.Google Scholar
Schimmerling, Ernest, The ABC’s of mice. Bulletin of Symbolic Logic, vol. 7 (2001), no. 4, pp. 485–503.Google Scholar
Shelah, Saharon, PCF without choice, ArXiv e-prints, (2010), [Sh:835]. arXiv:math/0510229.Google Scholar
Shi, Xianghui and Trang, Nam Duc, I 0and combinatorics at λ+, preprint, 20 pages, 2014.Google Scholar
Shore, Richard A. and Slaman, Theodore A., Defining the Turing jump. Mathematical Research Letter, vol. 6 (1999), no. 5–6, pp. 711–722.CrossRefGoogle Scholar
Slaman, Theodore A. and Steel, John R., Definable functions on degrees, Cabal Seminar 81–85, Lecture Notes in Mathematics, vol. 1333, Springer, Berlin, 1988, pp. 37–55.CrossRefGoogle Scholar
Slaman, Theodore A., Complementation in the Turing degrees, this Journal, vol. 54 (1989), no. 1, pp. 160–176.Google Scholar
Solovay, Robert, Woodin’s proof on sharps, handwritten notes, 1981.Google Scholar
Solovay, Robert M., Reinhardt, William N., and Kanamori, Akihiro, Strong axioms of infinity and elementary embeddings. Annals of Mathematical Logic, vol. 13 (1978), no. 1, pp. 73–116.Google Scholar
Steel, John R., HODL(R)is a core model below Θ. Bulletin of Symbolic Logic, vol. 1 (1995), no. 1, pp. 75–84.Google Scholar
Woodin, W. Hugh, Some consistency results in ZFC using AD, Cabal seminar 79–81, Lecture Notes in Mathematics, vol. 1019, Springer, Berlin, 1983, pp. 172–198.CrossRefGoogle Scholar
Woodin, W. Hugh, Notes on an AD-like axiom, July 6 1990. Seminar notes taken by George Kafkoulis.Google Scholar
Woodin, W. Hugh, Suitable extender models I. Journal of Mathematical Logic, vol. 10 (2010), no. 1–2, pp. 101–339.CrossRefGoogle Scholar
Woodin, W. Hugh, Suitable extender models II: beyond ω-huge. Journal of Mathematical Logic, vol. 11 (2011), no. 2, pp. 115–436.Google Scholar
Woodin, W. Hugh, The fine structure of suitable extender models I, 2014.Google Scholar
Yang, Sen, Prikry-type forcing and minimal α-degree. ArXiv e-prints, (2013). arXiv:1310.0891.Google Scholar