Article contents
Automorphism groups of arithmetically saturated models
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper we study the automorphism groups of countable arithmetically saturated models of Peano Arithmetic. The automorphism groups of such structures form a rich class of permutation groups. When studying the automorphism group of a model, one is interested to what extent a model is recoverable from its automorphism group. Kossak-Schmerl [12] show that if M is a countable, arithmetically saturated model of Peano Arithmetic, then Aut(M) codes SSy(M). Using that result they prove:
Let M1. M2 be countable arithmetically saturated models of Peano Arithmetic such that Aut(M1) ≅ Aut(M2). Then SSy(M1) = SSy(M2).
We show that if M is a countable arithmetically saturated of Peano Arithmetic, then Aut(M) can recognize if some maximal open subgroup is a stabilizer of a nonstandard element, which is smaller than any nonstandard definable element. That fact is used to show the main theorem:
Let M1, M2be countable arithmetically saturated models of Peano Arithmetic such that Aut(M1) ≅ Aut(M2). Then for every n < ω
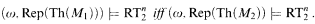
Here RT2n is Infinite Ramsey's Theorem stating that every 2-coloring of [ω]n has an infinite homogeneous set. Theorem 0.2 shows that for models of a false arithmetic the converse of Kossak-Schmerl Theorem 0.1 is not true. Using the results of Reverse Mathematics we obtain the following corollary:
There exist four countable arithmetically saturated models of Peano Arithmetic such that they have the same standard system but their automorphism groups are pairwise non-isomorphic.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2006
References
REFERENCES
- 7
- Cited by


