Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-29T00:42:48.811Z Has data issue: false hasContentIssue false
  • English
  • Français

AUTOMATIC AND POLYNOMIAL-TIME ALGEBRAIC STRUCTURES

Published online by Cambridge University Press:  29 April 2019

NIKOLAY BAZHENOV ,
MATTHEW HARRISON-TRAINOR ,
ISKANDER KALIMULLIN ,
ALEXANDER MELNIKOV  and
KENG MENG NG
NIKOLAY BAZHENOV
Affiliation:
SOBOLEV INSTITUTE OF MATHEMATICS NOVOSIBIRSK, RUSSIA and NOVOSIBIRSK STATE UNIVERSITY NOVOSIBIRSK, RUSSIA E-mail: [email protected]: http://bazhenov.droppages.com
MATTHEW HARRISON-TRAINOR
Affiliation:
DEPARTMENT OF PURE MATHEMATICS UNIVERSITY OF WATERLOO ON N2L 3G1, CANADA E-mail: [email protected]: http://www.math.uwaterloo.ca/∼maharris/
ISKANDER KALIMULLIN
Affiliation:
DEPARTMENT OF MATHEMATICS KAZAN FEDERAL UNIVERSITY KAZAN, RUSSIAE-mail: [email protected]
ALEXANDER MELNIKOV
Affiliation:
SCHOOL OF NATURAL AND COMPUTATIONAL SCIENCES MASSEY UNIVERSITY AUCKLAND, NEW ZEALAND E-mail: [email protected]
KENG MENG NG
Affiliation:
DIVISION OF MATHEMATICAL SCIENCES SCHOOL OF PHYSICAL AND MATHEMATICAL SCIENCES NANYANG TECHNOLOGICAL UNIVERSITY 21 NANYANG LINK, SINGAPORE637371E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A structure is automatic if its domain, functions, and relations are all regular languages. Using the fact that every automatic structure is decidable, in the literature many decision problems have been solved by giving an automatic presentation of a particular structure. Khoussainov and Nerode asked whether there is some way to tell whether a structure has, or does not have, an automatic presentation. 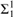We answer this question by showing that the set of Turing machines that represent automata-presentable structures is ${\rm{\Sigma }}_1^1 $-complete. We also use similar methods to show that there is no reasonable characterisation of the structures with a polynomial-time presentation in the sense of Nerode and Remmel.

Keywords

Primary 03C5703D05Secondary 03D2003D4503D8068Q45automatic structuresclassificationindex sets
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 4 , December 2019 , pp. 1630 - 1669
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abu Zaid, F., Grädel, E., and Reinhardt, F., Advice automatic structures and uniformly automatic classes, 26th EACSL Annual Conference on Computer Science Logic (CSL 2017) (Goranko, V. and Dam, M., editors), Leibniz International Proceedings in Informatics (LIPIcs), vol. 82, Schloss Dagstuhl–Leibniz-Zentrum für Informatik, Dagstuhl, Germany, 2017, pp. 35:1–35:20.Google Scholar
Alaev, P. E., Existence and uniqueness of structures computable in polynomial-time. Algebra and Logic, vol. 55 (2016), no. 1, pp. 72–76.CrossRefGoogle Scholar
Ash, C. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy, Studies in Logic and the Foundations of Mathematics, vol. 144, North-Holland, Amsterdam, 2000.Google Scholar
Bennett, C. H., Logical reversibility of computation. IBM Journal of Research and Development, vol. 17 (1973), pp. 525–532.CrossRefGoogle Scholar
Blumensath, A. and Grädel, E., Automatic structures, 15th Annual IEEE Symposium on Logic in Computer Science (Santa Barbara, CA, 2000) (Williams, A. D., editor), IEEE Computer Society Press, Los Alamitos, CA, 2000, pp. 51–62.Google Scholar
Braun, G. and Strüngmann, L., Breaking up finite automata presentable torsion-free abelian groups. International Journal of Algebra and Computation, vol. 21 (2011), no. 8, pp. 1463–1472.CrossRefGoogle Scholar
Brumleve, D., Hamkins, J. D., and Schlicht, P., The mate-in-n problem of infinite chess is decidable, How the World Computes (Cooper, S. B., Dawar, A., and Löwe, B., editors), Lecture Notes in Computer Science, vol. 7318, Springer, Heidelberg, 2012, pp. 78–88.CrossRefGoogle Scholar
Calvert, W., Fokina, E., Goncharov, S. S., Knight, J. F., Kudinov, O., Morozov, A. S., and Puzarenko, V., Index sets for classes of high rank structures, this Journal, vol. 72 (2007), no. 4, pp. 1418–1432.Google Scholar
Carson, J., Harizanov, V., Knight, J., Lange, K., McCoy, C., Morozov, A., Quinn, S., Safranski, C., and Wallbaum, J., Describing free groups. Transactions of the American Mathematical Society, vol. 364 (2012), no. 11, pp. 5715–5728.CrossRefGoogle Scholar
Cenzer, D., Downey, R. G., Remmel, J. B., and Uddin, Z., Space complexity of abelian groups. Archive for Mathematical Logic, vol. 48 (2009), no. 1, pp. 115–140.CrossRefGoogle Scholar
Cenzer, D. and Remmel, J., Polynomial-time versus recursive models. Annals of Pure and Applied Logic, vol. 54 (1991), no. 1, pp. 17–58.CrossRefGoogle Scholar
Cenzer, D. and Remmel, J., Feasibly categorical abelian groups, Feasible mathematics, II (Ithaca, NY, 1992) (Clote, P. and Remmel, J. B., editors), Progress in Computer Science and Applied Logic, vol. 13, Birkhäuser Boston, Boston, MA, 1995, pp. 91–153.CrossRefGoogle Scholar
Cenzer, D. and Remmel, J. B., Polynomial time versus computable boolean algebras, Recursion Theory and Complexity, Proceedings 1997 Kazan Workshop (Arslanov, M. and Lempp, S., editors), de Gruyter, Berlin, 1999, pp. 15–53.Google Scholar
Cenzer, D. A. and Remmel, J. B., Polynomial-time abelian groups. Annals of Pure and Applied Logic, vol. 56 (1992), no. 1–3, pp. 313–363.CrossRefGoogle Scholar
Delhommé, C., Automaticité des ordinaux et des graphes homogènes. Comptes rendus de l’Académie des Sciences Paris, vol. 339 (2004), no. 1, pp. 5–10.Google Scholar
Downey, R. and Melnikov, A. G., Computable completely decomposable groups. Transactions of the American Mathematical Society, vol. 366 (2014), no. 8, pp. 4243–4266.CrossRefGoogle Scholar
Downey, R. G., Kach, A. M., Lempp, S., Lewis-Pye, A. E. M., Montalbán, A., and Turetsky, D. D., The complexity of computable categoricity. Advances in Mathematics, vol. 268 (2015), pp. 423–466.CrossRefGoogle Scholar
Downey, R. G. and Montalbán, A., The isomorphism problem for torsion-free abelian groups is analytic complete. Journal of Algebra, vol. 320 (2008), no. 6, pp. 2291–2300.CrossRefGoogle Scholar
Epstein, D. B. A., Cannon, J. W., Holt, D. F., Levy, S. V. F., Paterson, M. S., and Thurston, W. P., Word Processing in Groups, Jones and Bartlett Publishers, Boston, MA, 1992.CrossRefGoogle Scholar
Ershov, Y. and Goncharov, S., Constructive Models, Siberian School of Algebra and Logic, Consultants Bureau, New York, 2000.CrossRefGoogle Scholar
Fokina, E. B., Index sets of decidable models. Sibirskii Matematicheskii Zhurnal, vol. 48 (2007), no. 5, pp. 1167–1179.Google Scholar
Fokina, E. B., Goncharov, S. S., Kharizanova, V., Kudinov, O. V., and Turetski, D., Index sets of n-decidable structures that are categorical with respect to m-decidable representations. Algebra Logika, vol. 54 (2015), no. 4, pp. 520–528, 544–545, 547–548.CrossRefGoogle Scholar
Fröhlich, A. and Shepherdson, J. C., Effective procedures in field theory. Philosophical Transactions of the Royal Society of London. Series A, vol. 248 (1956), pp. 407–432.CrossRefGoogle Scholar
Fuchs, L., Infinite Abelian Groups. vol. I, Pure and Applied Mathematics, vol. 36, Academic Press, New York, 1970.Google Scholar
Fuchs, L., Infinite Abelian Groups. vol. II, Pure and Applied Mathematics. vol. 36-II, Academic Press, New York, 1973.Google Scholar
Gončarov, S. S., The number of nonautoequivalent constructivizations. Algebra i Logika, vol. 16 (1977), no. 3, pp. 257–282, 377.Google Scholar
Goncharov, S. S., Bazhenov, N. A., and Marchuk, M. I., The index set of Boolean algebras that are autostable relative to strong constructivizations. Sibirskii Matematicheskii Zhurnal, vol. 56 (2015), no. 3, pp. 498–512.Google Scholar
Goncharov, S. S., Bazhenov, N. A., and Marchuk, M. I., Index sets of constructive models of natural classes that are autostable with respect to strong constructivizations. Doklady Akademii Nauk, vol. 464 (2015), no. 1, pp. 12–14.Google Scholar
Goncharov, S. S. and Naĭt, D., Computable structure and antistructure theorems. Algebra Logika, vol. 41 (2002), no. 6, pp. 639–681, 757.Google Scholar
Grigorieff, S., Every recursive linear ordering has a copy in dtime-space(n, log(n)), this Journal, vol. 55 (1990), no. 1, pp. 260–276.Google Scholar
Harrison, J., Recursive pseudo-well-orderings. Transactions of the American Mathematical Society, vol. 131 (1968), pp. 526–543.CrossRefGoogle Scholar
Harrison-Trainor, M., There is no classification of the decidably presentable structures. Journal of Mathematical Logic, vol. 18 (2018), no. 2, 1850010.CrossRefGoogle Scholar
Hjorth, G., The isomorphism relation on countable torsion free abelian groups. Fundamenta Mathematicae, vol. 175 (2002), no. 3, pp. 241–257.CrossRefGoogle Scholar
Hodgson, B. R., On direct products of automaton decidable theories. Theoretical Computer Science, vol. 19 (1982), no. 3, pp. 331–335.CrossRefGoogle Scholar
Jain, S., Khoussainov, B., and Stephan, F., Finitely generated semiautomatic groups. Computability, vol. 7 (2018), no. 2–3, pp. 273–287.CrossRefGoogle Scholar
Jain, S., Khoussainov, B., Stephan, F., Teng, D., and Zou, S., Semiautomatic structures. Theory of Computing Systems, vol. 61 (2017), no. 4, pp. 1254–1287.CrossRefGoogle Scholar
Kalimullin, I., Melnikov, A., and Ng, K. M., Algebraic structures computable without delay. Theoretical Computer Science, vol. 674 (2017), pp. 73–98.CrossRefGoogle Scholar
Kalimullin, I. S., Melnikov, A. G., and Ng, K. M., The diversity of categoricity without delay. Algebra and Logic, vol. 56 (2017), no. 2, pp. 171–177.CrossRefGoogle Scholar
Kharlampovich, O., Khoussainov, B., and Myasnikov, A., From automatic structures to automatic groups. Groups, Geometry, and Dynamics, vol. 8 (2014), no. 1, pp. 157–198.CrossRefGoogle Scholar
Khoussainov, B., Liu, J., and Minnes, M., Unary automatic graphs: An algorithmic perspective. Mathematical Structures in Computer Science, vol. 19 (2009), no. 1, pp. 133–152.CrossRefGoogle Scholar
Khoussainov, B. and Minnes, M., Model-theoretic complexity of automatic structures. Annals of Pure and Applied Logic, vol. 161 (2009), no. 3, pp. 416–426.CrossRefGoogle Scholar
Khoussainov, B. and Minnes, M., Three lectures on automatic structures, Logic Colloquium 2007 (Delon, F., Kohlenbach, U., Maddy, P., and Stephan, F., editors), Lecture Notes in Logic, vol. 35, Association for Symbolic Logic, La Jolla, CA, 2010, pp. 132–176.Google Scholar
Khoussainov, B. and Nerode, A., Automatic presentations of structures, Logic and Computational Complexity (Indianapolis, IN, 1994) (Leivant, D., editor), Lecture Notes in Computer Science, vol. 960, Springer, Berlin, 1995, pp. 367–392.CrossRefGoogle Scholar
Khoussainov, B. and Nerode, A., Open questions in the theory of automatic structures. Bulletin of the European Association for Theoretical Computer Science (EATCS), (2008), no. 94, pp. 181–204.Google Scholar
Khoussainov, B., Nies, A., Rubin, S., and Stephan, F., Automatic structures: Richness and limitations. Logical Methods in Computer Science, vol. 3 (2007), no. 2, pp. 2:2, 18.CrossRefGoogle Scholar
Khoussainov, B. and Rubin, S., Automatic structures: Overview and future directions. Journal of Automata, Languages and Combinatorics, vol. 8 (2003), no. 2, pp. 287–301.Google Scholar
Lachlan, A. H., On some games which are relevant to the theory of recursively enumerable sets. Annals of Mathematics (2), vol. 91 (1970), pp. 291–310.CrossRefGoogle Scholar
Lempp, S. and Slaman, T. A., The complexity of the index sets of $\aleph _0 $-categorical theories and of Ehrenfeucht theories, Advances in Logic (Gao, S., Jackson, S., and Zhang, Y., editors), Contemporary Mathematics, vol. 425, American Mathematical Society, Providence, RI, 2007, pp. 43–47.CrossRefGoogle Scholar
Lyndon, R. C. and Schupp, P. E., Combinatorial Group Theory, Classics in Mathematics, Springer-Verlag, Berlin, 2001, Reprinted of the 1977 edition.CrossRefGoogle Scholar
Mal’cev, A., Constructive algebras. I. Uspekhi Matematicheskikh Nauk, vol. 16 (1961), no. 3 (99), pp. 3–60.Google Scholar
McCoy, C. and Wallbaum, J., Describing free groups, Part II:${\rm{\Pi }}_4^0 $ hardness and no ${\rm{\Sigma }}_2^0 $ basis . Transactions of the American Mathematical Society , vol. 364 (2012), no. 11, pp. 5729–5734.CrossRefGoogle Scholar
Melnikov, A. G., Eliminating unbounded search in computable algebra, Unveiling Dynamics and Complexity (Kari, J., Manea, F., and Petre, I., editors), Lecture Notes in Computer Science, vol. 10307, Springer, Cham, 2017, pp. 77–87.CrossRefGoogle Scholar
Nerode, A. and Remmel, J. B., Polynomial time equivalence types, Logic and Computation (Pittsburgh, PA, 1987) (Sieg, W., editor), Contemporary Mathematics, vol. 106, American Mathematical Society, Providence, RI, 1990, pp. 221–249.CrossRefGoogle Scholar
Nies, A. and Semukhin, P., Finite automata presentable abelian groups. Annals of Pure and Applied Logic, vol. 161 (2009), no. 3, pp. 458–467.CrossRefGoogle Scholar
Nurtazin, A. T., Strong and weak constructivization and computable families. Algebra and Logic, vol. 13 (1974), no. 3, pp. 177–184.CrossRefGoogle Scholar
Oliver, G. P. and Thomas, R. M., Automatic presentations for finitely generated groups, STACS 2005 (Diekert, V. and Durand, B., editors), Lecture Notes in Computer Science, vol. 3404, Springer, Berlin, 2005, pp. 693–704.CrossRefGoogle Scholar
Rabin, M., Computable algebra, general theory and theory of computable fields. Transactions of the American Mathematical Society, vol. 95 (1960), pp. 341–360.Google Scholar
Riggs, K., The decomposability problem for torsion-free abelian groups is analytic complete. Proceedings of the American Mathematical Society, vol. 143 (2015), no. 8, pp. 3631–3640.CrossRefGoogle Scholar
Rogers, H., Theory of Recursive Functions and Effective Computability, second ed., MIT Press, Cambridge, MA, 1987.Google Scholar
Selivanov, V. L., Enumerations of families of general recursive functions. Algebra and Logic, vol. 15 (1976), no. 2, pp. 128–141.CrossRefGoogle Scholar
Soare, R., Recursively Enumerable Sets and Degrees, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1987, A study of computable functions and computably generated sets.CrossRefGoogle Scholar
Spector, C., Recursive well-orderings, this Journal, vol. 20 (1955), pp. 151–163.Google Scholar
Thomas, S., The classification problem for torsion-free abelian groups of finite rank. Journal of the American Mathematical Society, vol. 16 (2003), no. 1, pp. 233–258.CrossRefGoogle Scholar
Tsankov, T., The additive group of the rationals does not have an automatic presentation, this Journal, vol. 76 (2011), no. 4, pp. 1341–1351.Google Scholar
van der Waerden, B., Eine Bemerkung über die Unzerlegbarkeit von Polynomen. Mathematische Annalen, vol. 102 (1930), no. 1, pp. 738–739.CrossRefGoogle Scholar