No CrossRef data available.
Article contents
ASPERÓ–MOTA ITERATION AND THE SIZE OF THE CONTINUUM
Published online by Cambridge University Press: 02 May 2022
Abstract
In this paper we build an Asperó–Mota iteration of length 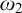 $\omega _2$ that adds a family of
$\omega _2$ that adds a family of 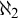 $\aleph _2$ many club subsets of
$\aleph _2$ many club subsets of 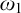 $\omega _1$ which cannot be diagonalized while preserving
$\omega _1$ which cannot be diagonalized while preserving 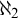 $\aleph _2$. This result discloses a technical limitation of some types of Asperó–Mota iterations.
$\aleph _2$. This result discloses a technical limitation of some types of Asperó–Mota iterations.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
Footnotes
The author is supported by Grant-in-Aid for Scientific Research (C) 18K03393, Japan Society for the Promotion of Science.



