Article contents
An elementary definability theorem for first order logic
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper, we will present a definability theorem for first order logic. This theorem is very easy to state, and its proof only uses elementary tools. To explain the theorem, let us first observe that if M is a model of a theory T in a language 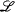 , then, clearly, any definable subset S ⊂ M (i.e., a subset S = {a ∣ M ⊨ φ(a)} defined by some formula φ) is invariant under all automorphisms of M. The same is of course true for subsets of Mn defined by formulas with n free variables.
, then, clearly, any definable subset S ⊂ M (i.e., a subset S = {a ∣ M ⊨ φ(a)} defined by some formula φ) is invariant under all automorphisms of M. The same is of course true for subsets of Mn defined by formulas with n free variables.
Our theorem states that, if one allows Boolean valued models, the converse holds. More precisely, for any theory T we will construct a Boolean valued model M, in which precisely the T -provable formulas hold, and in which every (Boolean valued) subset which is invariant under all automorphisms of M is definable by a formula 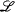 .
.
Our presentation is entirely selfcontained, and only requires familiarity with the most elementary properties of model theory. In particular, we have added a first section in which we review the basic definitions concerning Boolean valued models.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1999
References
REFERENCES
- 4
- Cited by


