Article contents
An effective selection theorem
Published online by Cambridge University Press: 12 March 2014
Extract
A recent result of J.P. Burgess [1] states:
Theorem 0. Let F be a multifunction from an analytic subset T of a Polish space to a Polish space X. If F is Borel measurable, Graph(F) is coanalytic in T × X and F(t) is nonmeager in its closure 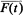 for each t Є T, then F admits a Borel measurable selector.
for each t Є T, then F admits a Borel measurable selector.
The above result unifies and significantly extends earlier results of H. Sarbadhikari [8], S.M. Srivastava [9] and G. Debs (unpublished). The reader is referred to [1] for details.
The aim of this article is to give an effective version of Theorem 0. We do this by proving a basis theorem for Π11 sets which are nonmeager in their closure and satisfy a local version of the measurability condition in Theorem 0. Our basis theorem generalizes a well-known result of P.G. Hinman [4] and S.K. Thomason [10] (see also [5] and [7, 4F.20]). Our methods are similar to those used by A. Louveau to prove that a 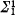 , σ-compact set is contained in a
, σ-compact set is contained in a  , σ-compact set (see [7, 4F.18]).
, σ-compact set (see [7, 4F.18]).
The paper is organized as follows. §2 is devoted to preliminaries. In §3, we prove the basis theorem and deduce as a consequence an effective version of Theorem 0. We show in §4 how our methods can be used to give alternative proofs of some known results.
Discussions with R. Barua, B.V. Rao and V.V. Srivatsa are gratefully acknowledged. I am indebted to J.P. Burgess for drawing my attention to an error in an earlier draft of this paper.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1982
References
REFERENCES
- 2
- Cited by


