Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brendle, Jörg
1995.
Combinatorial properties of classical forcing notions.
Annals of Pure and Applied Logic,
Vol. 73,
Issue. 2,
p.
143.
Ikegami, Daisuke
2009.
Projective absoluteness for Sacks forcing.
Archive for Mathematical Logic,
Vol. 48,
Issue. 7,
p.
679.
Ikegami, Daisuke
2010.
Forcing absoluteness and regularity properties.
Annals of Pure and Applied Logic,
Vol. 161,
Issue. 7,
p.
879.
Müller, Sandra
and
Schlicht, Philipp
2023.
Uniformization and internal absoluteness.
Proceedings of the American Mathematical Society,
Vol. 151,
Issue. 7,
p.
3089.


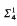 -Amoeba-absoluteness implies that
-Amoeba-absoluteness implies that 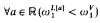 and, hence,
and, hence, 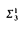 measurability. This answers a question of Haim Judah (private communication).
measurability. This answers a question of Haim Judah (private communication).