Article contents
Alternative proof of a theorem of Kleene
Published online by Cambridge University Press: 12 March 2014
Extract
We offer a simple alternative proof of Theorem II, Kleene [1]:
Theorem. For certain primitive recursive -predicates R and S,
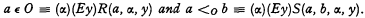
We separate the definitions of < o and O:
Definition 1. (1) 1 <o2; (2) for all y, if 1 <oy, then y <o 2v; (3) for all e, if (n)(Ey)T(e, no, y) and (n)(e(no) <oe((n+1)o)), then (n)(e(no) <o 3·5e); (4) for all x, y, z, if x <oy, y <oz, then x <oz; (5) a <ob only as required by (1)–(4).
Definition 2. a ϵ O if and only if 1 <o 2α.
If we write α(2a·3b) = O for a <ob in Conditions (1) to (4) of Definition 1 and take their conjunction, we get an arithmetic predicate P(α). By the Frege-Dedekind device for handling inductive definitions,

Hence, by Theorem 1 (Part 2) of [2], we have a primitive recursive S such that a <o b ≡ (α)(Ey)S(a, b, α, y). By Definition 2,
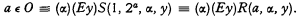
The classical use of the function quantifier (α) in the above proof is conspicuous. It is not clear that the constructive or intuitionistic content of Kleene's proof (cf. [1] Footnote 40) can be obtained by this method.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1958
References
REFERENCES
- 4
- Cited by


