Hostname: page-component-cc8bf7c57-hbs24 Total loading time: 0 Render date: 2024-12-11T23:06:47.518Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic semantics for quasi-classical modal logics

Published online by Cambridge University Press:  12 March 2014

W.J. Blok  and
P. Köhler
W.J. Blok*
Affiliation:
Simon Fraser University, Burnaby, B.C. Canada V5A 1S6
P. Köhler
Affiliation:
Justus-Liebig-Univerität, 6300 Giessen, Federal Republic of Germany
*
University of Illinois at Chicago, Box 4348, Chicago, Illinois 60680
Get access Rights & Permissions [Opens in a new window]

Extract

A well-known result, going back to the twenties, states that, under some reasonable assumptions, any logic can be characterized as the set of formulas satisfied by a matrix 〈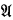, F〉, where 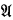is an algebra of the appropriate type, and F a subset of the domain of 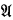, called the set of designated elements. In particular, every quasi-classical modal logic—a set of modal formulas, containing the smallest classical modal logic E, which is closed under the inference rules of substitution and modus ponens—is characterized by such a matrix, where 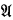now is a modal algebra, and F is a filter of 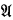. If the modal logic is in fact normal, then we can do away with the filter; we can study normal modal logics in the setting of varieties of modal algebras. This point of view was adopted already quite explicitly in McKinsey and Tarski [8]. The observation that the lattice of normal modal logics is dually isomorphic to the lattice of subvarieties of a variety of modal algebras paved the road for an algebraic study of normal modal logics. The algebraic approach made available some general results from Universal Algebra, notably those obtained by Jónsson [6], and thereby was able to contribute new insights in the realm of normal modal logics [2], [3], [4], [10].

The requirement that a modal logic be normal is rather a severe one, however, and many of the systems which have been considered in the literature do not meet it. For instance, of the five celebrated modal systems, S1–S5, introduced by Lewis, S4 and S5 are the only normal ones, while only SI fails to be quasi-classical. The purpose of this paper is to generalize the algebraic approach so as to be applicable not just to normal modal logics, but to quasi-classical modal logics in general.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 4 , December 1983 , pp. 941 - 964
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Balbes, R. and Dwinoer, P., Distributive lattices, University of Missouri, Columbia, 1974.Google Scholar
[2]Blok, W.J., The lattice of modal logics; an algebraic investigation, this Journal, vol. 45 (1980), pp. 221–236.Google Scholar
[3]Blok, W.J., On the degree of incompleteness of modal logics and the covering relation in the lattice of modal logics, Report 78–07, Univ. of Amsterdam, 1978.Google Scholar
[4]Blok, W.J., Pretabular varieties of modal algebras, Trends in Modal Logic, Studia Logica, vol. 39, no. 2/3, (1980), pp. 101–124.CrossRefGoogle Scholar
[5]Grätzer, G., Universal algebra, 2nd ed., Springer-Verlag, Berlin-Heidelberg-New York, 1979.CrossRefGoogle Scholar
[6]Jónsson, B., Algebras whose congruence lattices are distributive, Mathematica Scandinavica, vol. 21 (1967), pp. 110–121.CrossRefGoogle Scholar
[7]Makinson, D. and Segerberg, K., Post completeness and ultrafilters, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 20 (1974), pp. 385–388.CrossRefGoogle Scholar
[8]McKinsey, J.C.C. and Tarski, A., Some theorems about the sentential calculi of Lewis and Heyting, this Journal, vol. 13 (1948), pp. 1–15.Google Scholar
[9]Rautenberg, W., Klassische und nichtklassische Aussagenlogik, Vieweg, Braunschweig-Wiesbaden, 1979.CrossRefGoogle Scholar
[10]Rautenberg, W., Der Verband der normalen und verzweigten Modallogiken, Mathematische Zeitschrift, vol. 156 (1977), pp. 123–140.CrossRefGoogle Scholar
[11]Sambin, G. and Valentini, S., Post completeness and free algebras, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 26 (1980), pp. 343–347.CrossRefGoogle Scholar
[12]Segerberg, K., An essay in classical modal logic, Philosophical Studies, Uppsala, 1971.Google Scholar
[13]Segerberg, K., Post completeness in modal logic, this Journal, vol. 37 (1972), pp. 711–715.Google Scholar
[14]Segerberg, K., The truth about some Post numbers, this Journal, vol. 41 (1976), pp. 239–244.Google Scholar