Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dordal, Peter Lars
1989.
Towers in [ω]ω and ωω.
Annals of Pure and Applied Logic,
Vol. 45,
Issue. 3,
p.
247.
Nyikos, Peter J.
1990.
On first countable, countably compact spaces II: remainders in a van Douwen construction and P-ideals.
Topology and its Applications,
Vol. 35,
Issue. 2-3,
p.
185.
Nyikos, Peter J.
1992.
Subsets of ωω and the Fréchet-Urysohn and αi-properties.
Topology and its Applications,
Vol. 48,
Issue. 2,
p.
91.
Brendle, Jörg
Judah, Haim
and
Shelah, Saharon
1992.
Combinatorial properties of Hechler forcing.
Annals of Pure and Applied Logic,
Vol. 58,
Issue. 3,
p.
185.
Spinas, O.
1992.
Iterated forcing in quadratic form theory.
Israel Journal of Mathematics,
Vol. 79,
Issue. 2-3,
p.
297.
Kamburelis, A.
and
W’glorz, B.
1996.
Splittings.
Archive for Mathematical Logic,
Vol. 35,
Issue. 4,
p.
263.
Spinas, Otmar
1997.
Partition numbers.
Annals of Pure and Applied Logic,
Vol. 90,
Issue. 1-3,
p.
243.
Miller, Arnold W.
2005.
The γ-borel conjecture.
Archive for Mathematical Logic,
Vol. 44,
Issue. 4,
p.
425.
Brendle, Jörg
and
Yatabe, Shunsuke
2005.
Forcing indestructibility of MAD families.
Annals of Pure and Applied Logic,
Vol. 132,
Issue. 2-3,
p.
271.
Brendle, Jörg
2006.
Van Douwen’s diagram for dense sets of rationals.
Annals of Pure and Applied Logic,
Vol. 143,
Issue. 1-3,
p.
54.
Brendle, Jörg
2007.
Distinguishing groupwise density numbers.
Monatshefte für Mathematik,
Vol. 152,
Issue. 3,
p.
207.
Hernández-Hernández, Fernando
and
Hrušák, Michael
2007.
Cardinal Invariants of AnalyticP-Ideals.
Canadian Journal of Mathematics,
Vol. 59,
Issue. 3,
p.
575.
Minami, Hiroaki
2010.
Around splitting and reaping for partitions of ω.
Archive for Mathematical Logic,
Vol. 49,
Issue. 4,
p.
501.
Blass, Andreas
2010.
Handbook of Set Theory.
p.
395.
BRENDLE, Jörg
and
LÖWE, Benedikt
2011.
Eventually different functions and inaccessible cardinals.
Journal of the Mathematical Society of Japan,
Vol. 63,
Issue. 1,
Dow, Alan
and
Pichardo-Mendoza, Roberto
2013.
Efimovʼs problem and Boolean algebras.
Topology and its Applications,
Vol. 160,
Issue. 17,
p.
2207.
Fischer, Vera
Friedman, Sy David
and
Khomskii, Yurii
2013.
Co-analytic mad families and definable wellorders.
Archive for Mathematical Logic,
Vol. 52,
Issue. 7-8,
p.
809.
Hrušák, Michael
and
Minami, Hiroaki
2014.
Mathias–Prikry and Laver–Prikry type forcing.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 3,
p.
880.
Brendle, Jörg
and
Raghavan, Dilip
2014.
Bounding, splitting, and almost disjointness.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 2,
p.
631.
Hrušák, M.
and
Ramos-García, U.A.
2014.
Malykhin's problem.
Advances in Mathematics,
Vol. 262,
Issue. ,
p.
193.


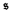 (and hence the distributivity number
(and hence the distributivity number 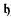 ) remains at
) remains at 