Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T02:33:11.021Z Has data issue: false hasContentIssue false
  • English
  • Français

ZF ⊦ Σ40 determinateness

Published online by Cambridge University Press:  12 March 2014

J. B. Paris
J. B. Paris*
Affiliation:
Manchester University, Manchester, England
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we show that in Zermelo-Fraenkel set theory (ZF) 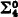sets of reals are determinate.

Before proceeding to the proof it will be helpful to consider some previous work in this area. The first major result was obtained by Gale and Stewart [3] who showed that in ZF open games are determinate. This was then successively improved by Wolfe [4] to 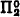(and so of course 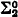) and then by Morton Davis [1] to 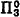. The results of Morton Davis further showed that countable unions of sufficiently ‘simple’ determinate sets are also determinate. At this time, however, 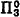sets did not appear sufficiently simple for this method to be applied in order to get 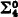determinacy.

The next major advance was made by D. A. Martin who showed, using indiscernibles, that with large cardinal assumptions 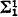games are equivalent to certain open games (i.e., player I (II) has a winning strategy for the 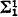game iff I (II) has a winning strategy for the open game). Thus, by the Gale–Stewart result, 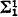games are determinate. Martin's result also showed that under these large cardinal assumptions 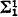sets are sufficiently simple for the Morton Davis method to be applied to them.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 37 , Issue 4 , December 1972 , pp. 661 - 667
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Davis, M., Infinite games with perfect Information, Advances in game theory, Annals of Mathematical Studies, No. 52, Princeton University Press, Princeton, N.J., 1964, pp. 85–101.Google Scholar
[2]Friedman, H., Higher set theory and mathematical practice, Annals of Mathematical Logic, vol. 2 (1971).CrossRefGoogle Scholar
[3]Gale, D. and Stewart, F. M., Infinite games with information, Contributions to the theory of games, Annals of Mathematical Studies, No. 28, Princeton University Press, Princeton, N.J., 1953, pp. 245–266.Google Scholar
[4]Wolfe, P., The strict determinateness of certain infinite games, Pacific Journal of Mathematics, vol. 5 (1955), pp. 841–847.CrossRefGoogle Scholar