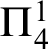 ${\Pi }^{1}_{4}$-STATEMENTS: A PILOT STUDY
${\Pi }^{1}_{4}$-STATEMENTS: A PILOT STUDYPublished online by Cambridge University Press: 16 February 2021
In previous work, the author has shown that 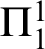 $\Pi ^1_1$
-induction along
$\Pi ^1_1$
-induction along 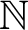 $\mathbb N$
is equivalent to a suitable formalization of the statement that every normal function on the ordinals has a fixed point. More precisely, this was proved for a representation of normal functions in terms of Girard’s dilators, which are particularly uniform transformations of well orders. The present paper works on the next type level and considers uniform transformations of dilators, which are called 2-ptykes. We show that
$\mathbb N$
is equivalent to a suitable formalization of the statement that every normal function on the ordinals has a fixed point. More precisely, this was proved for a representation of normal functions in terms of Girard’s dilators, which are particularly uniform transformations of well orders. The present paper works on the next type level and considers uniform transformations of dilators, which are called 2-ptykes. We show that 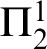 $\Pi ^1_2$
-induction along
$\Pi ^1_2$
-induction along 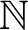 $\mathbb N$
is equivalent to the existence of fixed points for all 2-ptykes that satisfy a certain normality condition. Beyond this specific result, the paper paves the way for the analysis of further
$\mathbb N$
is equivalent to the existence of fixed points for all 2-ptykes that satisfy a certain normality condition. Beyond this specific result, the paper paves the way for the analysis of further 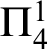 $\Pi ^1_4$
-statements in terms of well ordering principles.
$\Pi ^1_4$
-statements in terms of well ordering principles.
 ${\boldsymbol{\varPi}}_{\mathbf{1}}^{\mathbf{1}}$
-comprehension
, Ph.D. thesis, University of Leeds, 2018, available at http://etheses.whiterose.ac.uk/20929/.Google Scholar
${\boldsymbol{\varPi}}_{\mathbf{1}}^{\mathbf{1}}$
-comprehension
, Ph.D. thesis, University of Leeds, 2018, available at http://etheses.whiterose.ac.uk/20929/.Google Scholar ${\boldsymbol{\varPi}}_{\mathbf{1}}^{\mathbf{1}}$
-comprehension
${\boldsymbol{\varPi}}_{\mathbf{1}}^{\mathbf{1}}$
-comprehension