Article contents
Weak compactness and square bracket partition relations
Published online by Cambridge University Press: 12 March 2014
Extract
Although there are many characterizations of weakly compact cardinals (e.g. in terms of indescnbability and tree properties as well as compactness) the most interesting set-theoretic (combinatorial) one is in terms of partition relations. To be more precise we define for κ and α cardinals and n an integer the partition relation 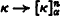 of Erdös, Hajnal and Rado [2] as follows:
of Erdös, Hajnal and Rado [2] as follows:
For every function F: [κ]n→ α (called a partition of [κ]n, the n-element subsets of κ, into α pieces), there exists a set C⊆ κ (called homogeneous for F) such that card C = κ and F″[C]n≠ α, i.e. some element of the range is omitted when F is restricted to the n-element subsets of C. It is the simplest (nontrivial) of these relations, i.e.  , that is the well-known equivalent of weak compactness.1
, that is the well-known equivalent of weak compactness.1
Two directions of inquiry immediately suggest themselves when weak compactness is described in terms of these partition relations: (a) Trying to strengthen the relation by increasing the superscript—e.g., 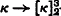 —and (b) trying to weaken the relation by increasing the subscript—e.g.,
—and (b) trying to weaken the relation by increasing the subscript—e.g., 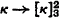 . As it turns out, the strengthening to
. As it turns out, the strengthening to 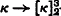 is only illusory for using the equivalence of
is only illusory for using the equivalence of  to the tree property one quickly sees that
to the tree property one quickly sees that  implies (and so is equivalent to)
implies (and so is equivalent to) 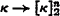 for every n. Thus
for every n. Thus  is the strongest of these partition relations. The second question seems much more difficult.
is the strongest of these partition relations. The second question seems much more difficult.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
References
BIBLIOGRAPHY
- 3
- Cited by


