Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T02:09:22.002Z Has data issue: false hasContentIssue false
  • English
  • Français

WEAK CANONICAL BASES IN NSOP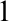$_1$ THEORIES

Part of: Model theory

Published online by Cambridge University Press:  11 June 2021

BYUNGHAN KIM
BYUNGHAN KIM*
Affiliation:
DEPARTMENT OF MATHEMATICS YONSEI UNIVERSITYSEOUL, SOUTH KOREAE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the notion of weak canonical bases in an NSOP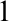 $_{1}$ theory T with existence. Given 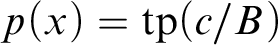$p(x)=\operatorname {tp}(c/B)$ where 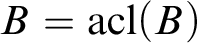$B=\operatorname {acl}(B)$ in 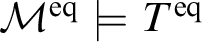${\mathcal M}^{\operatorname {eq}}\models T^{\operatorname {eq}}$ , the weak canonical base of p is the smallest algebraically closed subset of B over which p does not Kim-fork. With this aim we firstly show that the transitive closure $\approx $ of collinearity of an indiscernible sequence is type-definable. 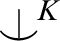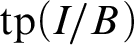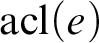Secondly, we prove that given a total $\mathop {\smile \hskip -0.9em ^| \ }^K$ -Morley sequence I in p, the weak canonical base of $\operatorname {tp}(I/B)$ is $\operatorname {acl}(e)$ , if the hyperimaginary 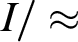$I/\approx $ is eliminable to e, a sequence of imaginaries. We also supply a couple of criteria for when the weak canonical base of p exists. In particular the weak canonical base of p is (if exists) the intersection of the weak canonical bases of all total 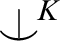$\mathop {\smile \hskip -0.9em ^| \ }^K$ -Morley sequences in p over B. 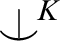However, while we investigate some examples, we point out that given two weak canonical bases of total $\mathop {\smile \hskip -0.9em ^| \ }^K$ -Morley sequences in p need not be interalgebraic, contrary to the case of simple theories. Lastly we suggest an independence relation relying on weak canonical bases, when T has those. The relation, satisfying transitivity and base monotonicity, might be useful in further studies on NSOP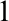 $_1$ theories .

Keywords

weak canonical basesNSOP1 theoriescollinearity

MSC classification

Primary: 03C45: Classification theory, stability and related concepts
Secondary: 03C50: Models with special properties (saturated, rigid, etc.)
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 3 , September 2021 , pp. 1259 - 1281
Check for updates
Copyright
© Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adler, H., A geometric introduction to forking and thorn-forking . Journal of Mathematical Logic , vol. 9 (2009), pp. 1–20.CrossRefGoogle Scholar
Adler, H., Explanations of independence, Ph.D. thesis, University of Freiburg, 2005.Google Scholar
Buechler, S., Canonical bases in some supersimple theories, unpublished, 1997.Google Scholar
Chatzidakis, Z., Properties of forking in $\omega$ -free pseudo-algebraically closed fields, this Journal, vol. 67 (2002), pp. 957–996.Google Scholar
Chernikov, A., Kim, B., and Ramsey, N., Transitivity, lowness, and ranks in NSOP ${}_1$ theories, preprint, 2020, arXiv:2006.10486.Google Scholar
Dobrowolski, J., Kim, B., and Ramsey, N, Independence over arbitrary sets in NSOP ${}_1$ theories, preprint, 2019, arXiv:1909.08368.Google Scholar
Granger, N., Stability, simplicity and the model theory of bilinear forms, Ph.D. thesis, University of Manchester, 1999.Google Scholar
Hart, B., Kim, B., and Pillay, A., Coordinatization and canonical bases in simple theories, this Journal, vol. 65 (2000), pp. 293–309.Google Scholar
Hodge, W., Model Theory, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
Kaplan, I. and Ramsey, N., On Kim-independence. Journal of European Mathematical Society, vol. 22 (2020), pp. 1423–1474.Google Scholar
Kaplan, I. and Ramsey, N., Transitivity of Kim-independence . Advances in Mathematics , vol. 397 (2021), p. 107573.CrossRefGoogle Scholar
Kim, B., Simplicity Theory , Oxford University Press, Oxford, 2014.Google Scholar
Kim, B., Kim, H., and Scow, L., Tree indiscernibilities, revisited. Archive for Mathematical Logic, vol. 53 (2014), pp. 211–232.CrossRefGoogle Scholar
Kruckman, A. and Ramey, N., Generic expansion and Skolemization in NSOP ${}_1$ theories. Annals of Pure and Applied Logic, vol. 169 (2018), pp. 755–774.CrossRefGoogle Scholar
Shelah, S., Simple unstable theories. Annals of Mathematical Logic, vol. 19 (1980), pp. 177–203.CrossRefGoogle Scholar
Shelah, S., Toward classifying unstable theories . Annals of Pure and Applied Logic, vol. 80 (1996), pp. 229–255.CrossRefGoogle Scholar