Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T09:27:45.677Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIVERSAL COUNTABLE BOREL QUASI-ORDERS

Published online by Cambridge University Press:  18 August 2014

JAY WILLIAMS
JAY WILLIAMS*
Affiliation:
DEPARTMENT OF MATHEMATICS CALIFORNIA INSTITUTE OF TECHNOLOGY PASADENA, CA 91125, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In recent years, much work in descriptive set theory has been focused on the Borel complexity of naturally occurring classification problems, in particular, the study of countable Borel equivalence relations and their structure under the quasi-order of Borel reducibility. Following the approach of Louveau and Rosendal for the study of analytic equivalence relations, we study countable Borel quasi-orders.

In this paper we are concerned with universal countable Borel quasi-orders, i.e., countable Borel quasi-orders above all other countable Borel quasi-orders with regard to Borel reducibility. We first establish that there is a universal countable Borel quasi-order, and then establish that several countable Borel quasi-orders are universal. An important example is an embeddability relation on descriptive set theoretic trees.

Our main result states that embeddability of finitely generated groups is a universal countable Borel quasi-order, answering a question of Louveau and Rosendal. This immediately implies that biembeddability of finitely generated groups is a universal countable Borel equivalence relation. The same techniques are also used to show that embeddability of countable groups is a universal analytic quasi-order.

Finally, we show that, up to Borel bireducibility, there are 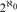${2^{{\aleph _0}}}$ distinct countable Borel quasi-orders, which symmetrize to a universal countable Borel equivalence relation.

Keywords

Borel equivalence relationsquasi-ordersmonoidsgroup theorysmall cancellation
Type
Articles
Information
The Journal of Symbolic Logic , Volume 79 , Issue 3 , September 2014 , pp. 928 - 954
Copyright
Copyright © The Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adams, Scot and Kechris, Alexander S., Linear algebraic groups and countable Borel equivalence relations. Journal of American Mathematical Society, vol. 13 (2000), no. 4, pp. 909–943.Google Scholar
Champetier, Christophe, L’espace des groupes de type fini. Topology, vol. 39 (2000), no. 4, pp. 657–680.CrossRefGoogle Scholar
Dougherty, R., Jackson, S., and Kechris, A. S., The structure of hyperfinite Borel equivalence relations. Transactions of the American Mathematical Society, vol. 341 (1994), no. 1, pp. 193–225.Google Scholar
Dougherty, Randall and Kechris, Alexander S., How many Turing degrees are there? Computability theory and its applications (Boulder, CO, 1999), Contemporary Mathematics, vol. 257, American Mathematical Society, Providence, RI, 2000, pp. 83–94.Google Scholar
Feldman, Jacob and Moore, Calvin C., Ergodic equivalence relations, cohomology, and von Neumann algebras. I. Transactions of the American Mathematical Society, vol. 234 (1977), no. 2, pp. 289–324Google Scholar
Friedman, Sy-David and Ros, Luca Motto, Analytic equivalence relations and bi-embeddability. this Journal, vol. 76 (2011), no. 1, pp. 243–266.Google Scholar
Gao, Su, Coding subset shift by subgroup conjugacy. Bulletin of the London Mathematical Society, vol. 32 (2000), no. 6, pp. 653–657.Google Scholar
Kechris, Alexander S., Classical descriptive set theorzy. Graduate Texts in Mathematics, vol. 156, Springer-Verlag, New York, 1995.Google Scholar
Louveau, Alain and Rosendal, Christian, Complete analytic equivalence relations. Transactions of the American Mathematical Society, vol. 357 (2005), no. 12, pp. 4839–4866.CrossRefGoogle Scholar
Lyndon, Roger C. and Schupp, Paul E., Combinatorial group theory. Classics in Mathematics, Springer-Verlag, Berlin, 2001. Reprint of the 1977 edition.Google Scholar
Mekler, Alan H., Stability of nilpotent groups of class 2 and prime exponent. this Journal, vol. 46 (1981), no. 4, pp. 781–788.Google Scholar
Thomas, Simon and Velickovic, Boban, On the complexity of the isomorphism relation for finitely generated groups. Journal of Algebra, vol. 217 (1999), no. 1, pp. 352–373.Google Scholar