Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-20T04:41:39.307Z Has data issue: false hasContentIssue false
  • English
  • Français

THE UNITY AND IDENTITY OF DECIDABLE OBJECTS AND DOUBLE-NEGATION SHEAVES

Published online by Cambridge University Press:  21 December 2018

MATÍAS MENNI
MATÍAS MENNI*
Affiliation:
CONICET AND UNIVERSIDAD NACIONAL DE LA PLATA LA PLATA1900ARGENTINAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

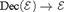Let ${\cal E}$ be a topos, ${\rm{Dec}}\left( {\cal E} \right) \to {\cal E}$ be the full subcategory of decidable objects, and 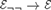${{\cal E}_{\neg \,\,\neg }} \to {\cal E}$ be the full subcategory of double-negation sheaves. We give sufficient conditions for the existence of a Unity and Identity 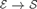${\cal E} \to {\cal S}$ for the two subcategories of ${\cal E}$ above, making them Adjointly Opposite. Typical examples of such ${\cal E}$ include many ‘gros’ toposes in Algebraic Geometry, simplicial sets and other toposes of ‘combinatorial’ spaces in Algebraic Topology, and certain models of Synthetic Differential Geometry.

Keywords

18B2518F9903E99axiomatic cohesiontopos theoryset theory
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 4 , December 2018 , pp. 1667 - 1679
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Carboni, A. and Janelidze, G., Decidable (= separable) objects and morphisms in lextensive categories.Journal of Pure and Applied Algebra, vol. 110 (1996), no. 3, pp. 219–240.CrossRefGoogle Scholar
Johnstone, P. T., Sketches of an Elephant: A Topos Theory Compendium, Oxford Logic Guides, vol. 43–44, The Clarendon Press Oxford University Press, New York, 2002.Google Scholar
Johnstone, P. T., Remarks on punctual local connectedness. Theory and Applications of Categories, vol. 25 (2011), pp. 51–63.Google Scholar
Kock, A., Synthetic Differential Geometry, second ed., Cambridge University Press, Cambridge, 2006.CrossRefGoogle Scholar
Lawvere, F. W., Cohesive toposes and Cantor’s “lauter Einsen”. Philosophy of Mathematics, vol. 2 (1994), no. 1, pp. 5–15.CrossRefGoogle Scholar
Lawvere, F. W., Unity and identity of opposites in calculus and physics. Applied Categorical Structures, vol. 4 (1996), pp. 167–174.CrossRefGoogle Scholar
Lawvere, F. W., Foundations and applications: Axiomatization and education. Bulletin of Symbolic Logic, vol. 9 (2003), no. 2, pp. 213–224.CrossRefGoogle Scholar
Lawvere, F. W., Axiomatic cohesion. Theory and Applications of Categories, vol. 19 (2007), pp. 41–49.Google Scholar
Lawvere, F. W., Core varieties, extensivity, and rig geometry. Theory and Applications of Categories, vol. 20 (2008), no. 14, pp. 497–503.Google Scholar
Lawvere, F. W. and Menni, M., Internal choice holds in the discrete part of any cohesive topos satisfying stable connected codiscreteness. Theory and Applications of Categories, vol. 30 (2015), pp. 909–932.Google Scholar
Lawvere, F. W. and Rosebrugh, R., Sets for Mathematics, Cambridge University Press, Cambridge, 2003.CrossRefGoogle Scholar
Marmolejo, F. and Menni, M., On the relation between continuous and combinatorial. Journal of Homotopy and Related Structures, vol. 12 (2017), no. 2, pp. 379–412.CrossRefGoogle Scholar
McLarty, C., Elementary axioms for canonical points of toposes, this Journal, vol. 52 (1987), no. 1, pp. 202–204.Google Scholar
McLarty, C., Defining sets as sets of points of spaces. Journal of Philosophical Logic, vol. 17 (1988), no. 1, pp. 75–90.CrossRefGoogle Scholar
Menni, M., Continuous cohesion over sets. Theory and Applications of Categories, vol. 29 (2014), pp. 542–568.Google Scholar
Menni, M., Sufficient cohesion over atomic toposes. Cahiers de Topologie et Geometrie Differentielle Categoriques, vol. 55 (2014), no. 2, pp. 113–149.Google Scholar
Menni, M., The construction of π0 in Axiomatic Cohesion.Tbilisi Mathematical Journal , vol. 10 (2017), no. 3, pp. 183–207.CrossRefGoogle Scholar