Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T16:23:16.486Z Has data issue: false hasContentIssue false
  • English
  • Français

Unique decomposition in classifiable theories

Published online by Cambridge University Press:  12 March 2014

Bradd Hart ,
Ehud Hrushovski  and
Michael C. Laskowski
Bradd Hart
Affiliation:
Department of Mathematics and Statistics, Mcmaster University, Hamilton, Ontario, Canada, L8S 4K1, E-mail: [email protected]
Ehud Hrushovski
Affiliation:
Institute of Mathematics, The Hebrew University of Jerusalem, 91904, Israel, E-mail: [email protected]
Michael C. Laskowski
Affiliation:
Mathematics Department, University of Maryland, College Park, MD 20742-4015, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

By a classifiable theory we shall mean a theory which is superstable, without the dimensional order property, which has prime models over pairs. In order to define what we mean by unique decomposition, we remind the reader of several definitions and results. We adopt the usual conventions of stability theory and work inside a large saturated model of a fixed classifiable theory T; for instance, if we write M ⊆ N for models of T, M and N we are thinking of these models as elementary submodels of this fixed saturated models; so, in particular, M is an elementary submodel of N. Although the results will not depend on it, we will assume that T is countable to ease notation.

We do adopt one piece of notation which is not completely standard: if T is classifiable, M0 ⊆ Mi for i = 1, 2 are models of T and M1 is independent from M2 over M0 then we write M1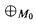M2 for the prime model over M1 ∪ M2.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 1 , March 2002 , pp. 61 - 68
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Buechler, S. and Shelah, S., On the existence of regular types, Annals of Pure and Applied Logic, vol. 45 (1989), pp. 277–308.Google Scholar
[2]Hart, B., Hrushovski, E., and Laskowski, M. C., The uncountable spectra of countable theories: the counting, in preparation.Google Scholar
[3]Shelah, S., Classification theory, North-Holland, 1990.Google Scholar