No CrossRef data available.
Article contents
Two arithmetical techniques with numbered classes
Published online by Cambridge University Press: 12 March 2014
Extract
If numbers be used to designate classes, there can be derived from a conjunct of classes numbers corresponding to the expanded product classes.
For example, let the product classes ābc and āb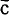 be designated by numbers I and 5 as in the following matrix:
be designated by numbers I and 5 as in the following matrix:

By using 1 (20) instead of a, 2 (21) instead of b, 4 (22) instead of c, etc., the following relationship emerges between the designation of the conjunct of classes (take 12) and the product classes (I and 5): the product class(es) of any conjunct of classes is (are) (1) the sum of any negated class numbers and (2) seven less the sum of any unnegated class numbers.
- Type
- Reviews
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1962
References
1 Product class numbers will be italicized to avoid confusion with class numbers.
2 1, 2, and 6, as well as various other combinations, will also serve; but 1, 2, and 7 seems to be the simplest which still invalidates all (pseudo-) syllogisms repeating the middle term in the conclusion.


