No CrossRef data available.
Article contents
A TOPOMETRIC EFFROS THEOREM
Published online by Cambridge University Press: 02 February 2023
Abstract
Given a continuous and isometric action of a Polish group G on an adequate Polish topometric space 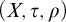 $(X,\tau ,\rho )$ and
$(X,\tau ,\rho )$ and 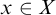 $x \in X$, we find a necessary and sufficient condition for
$x \in X$, we find a necessary and sufficient condition for 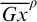 $\overline {Gx}^{\rho }$ to be co-meagre; we also obtain a criterion that characterizes when such a point exists. This work completes a criterion established in earlier work of the authors.
$\overline {Gx}^{\rho }$ to be co-meagre; we also obtain a criterion that characterizes when such a point exists. This work completes a criterion established in earlier work of the authors.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
Ben Yaacov, I.,
Topometric spaces and perturbations of metric structures
.
Logic and Analysis
, vol. 1 (2008), nos. 3–4, 235–272.CrossRefGoogle Scholar
Ben Yaacov, I., Berenstein, A., and Melleray, J.,
Polish topometric groups
.
Transactions of the American Mathematical Society
, vol. 365 (2013), no. 7, pp. 3877–3897.CrossRefGoogle Scholar
Ben Yaacov, I. and Melleray, J., Grey subsets of Polish spaces, this Journal, vol. 80 (2015), no. 4, pp. 1379–1397.Google Scholar
Berenstein, A., Henson, C. W., and Ibarlucía, T., Existentially closed measure-preserving actions of free groups, preprint, 2022, arXiv:2203.10178.Google Scholar
Gao, S.,
Invariant Descriptive Set Theory
, Pure and Applied Mathematics (Boca Raton), CRC Press, Boca Raton, 2009.Google Scholar



