Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-15T03:22:37.106Z Has data issue: false hasContentIssue false
  • English
  • Français

TOPOLOGICAL COMPLETENESS OF LOGICS ABOVE S4

Published online by Cambridge University Press:  22 April 2015

GURAM BEZHANISHVILI ,
DAVID GABELAIA  and
JOEL LUCERO-BRYAN
GURAM BEZHANISHVILI
Affiliation:
DEPARTMENT OF MATHEMATICAL SCIENCES NEW MEXICO STATE UNIVERSITY LAS CRUCES NM 88003, USAE-mail: [email protected]
DAVID GABELAIA
Affiliation:
A. RAZMADZE MATHEMATICAL INSTITUTE TBILISI STATE UNIVERSITY UNIVERSITY ST. 2, TBILISI 0186, GEORGIAE-mail: [email protected]
JOEL LUCERO-BRYAN
Affiliation:
DEPARTMENT OF APPLIED MATHEMATICS AND SCIENCES, KHALIFA UNIVERSITY ABU DHABI, UAEE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is a celebrated result of McKinsey and Tarski [28] that S4 is the logic of the closure algebra Χ+ over any dense-in-itself separable metrizable space. In particular, S4 is the logic of the closure algebra over the reals R, the rationals Q, or the Cantor space C. By [5], each logic above S4 that has the finite model property is the logic of a subalgebra of Q+, as well as the logic of a subalgebra of C+. This is no longer true for R, and the main result of [5] states that each connected logic above S4 with the finite model property is the logic of a subalgebra of the closure algebra R+.

In this paper we extend these results to all logics above S4. Namely, for a normal modal logic L, we prove that the following conditions are equivalent: (i) L is above S4, (ii) L is the logic of a subalgebra of Q+, (iii) L is the logic of a subalgebra of C+. We introduce the concept of a well-connected logic above S4 and prove that the following conditions are equivalent: (i) L is a well-connected logic, (ii) L is the logic of a subalgebra of the closure algebra $\xi _2^ + $ over the infinite binary tree, (iii) L is the logic of a subalgebra of the closure algebra 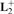${\bf{L}}_2^ + $ over the infinite binary tree with limits equipped with the Scott topology. Finally, we prove that a logic L above S4 is connected iff L is the logic of a subalgebra of R+, and transfer our results to the setting of intermediate logics.

Proving these general completeness results requires new tools. We introduce the countable general frame property (CGFP) and prove that each normal modal logic has the CGFP. We introduce general topological semantics for S4, which generalizes topological semantics the same way general frame semantics generalizes Kripke semantics. We prove that the categories of descriptive frames for S4 and descriptive spaces are isomorphic. It follows that every logic above S4 is complete with respect to the corresponding class of descriptive spaces. We provide several ways of realizing the infinite binary tree with limits, and prove that when equipped with the Scott topology, it is an interior image of both C and R. Finally, we introduce gluing of general spaces and prove that the space obtained by appropriate gluing involving certain quotients of L2 is an interior image of R.

Keywords

03B4503B55Modal logictopological semanticscompletenesscountable model propertyinfinite binary treeintuitionistic logic
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 2 , June 2015 , pp. 520 - 566
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aiello, M., van Benthem, J., and Bezhanishvili, G., Reasoning about space: The modal way. Journal of Logic and Computation, vol. 13 (2003), no. 6, pp. 889–920.Google Scholar
van Benthem, J., Bezhanishvili, G., and Gehrke, M., Euclidean hierarchy in modal logic. Studia Logica, vol. 75 (2003), no. 3, pp. 327–344.Google Scholar
van Benthem, J., Bezhanishvili, G., ten Cate, B., and Sarenac, D., Multimodal logics of products of topologies. Studia Logica, vol. 84 (2006), no. 3, pp. 369–392.Google Scholar
Bezhanishvili, G. and Bezhanishvili, N., Profinite Heyting algebras. Order, vol. 25 (2008), no. 3, pp. 211–227.Google Scholar
Bezhanishvili, G. and Gabelaia, D., Connected modal logics. Archive for Mathematical Logic, vol. 50 (2011), no. 2, pp. 287–317.Google Scholar
Bezhanishvili, G. and Gehrke, M., A New Proof of Completeness of S4 with Respect to the Real Line, PP-2002-06, University of Amsterdam, 2002.Google Scholar
Bezhanishvili, G. and Gehrke, M., Completeness of S4 with respect to the real line: revisited. Annals of Pure and Applied Logic, vol. 131 (2005), no. 1–3, pp. 287–301.Google Scholar
Bezhanishvili, G. and Lucero-Bryan, J., More on d-logics of subspaces of the rational numbers. Notre Dame Journal of Formal Logic, vol. 53(2012), no. 3, pp. 319–345.Google Scholar
Bezhanishvili, G., Mines, R., and Morandi, P. J., Topo-canonical completions of closure algebras and Heyting algebras. Algebra Universalis, vol. 58 (2008), no. 1, pp. 1–34.Google Scholar
Bezhanishvili, G. and Morandi, P. J., Priestley rings and Priestley order-compactifications. Order, vol. 28 (2011), no. 3, pp. 399–413.CrossRefGoogle Scholar
Blackburn, P., de Rijke, M., and Venema, Y.. Modal Logic, Cambridge University Press, Cambridge, 2001.Google Scholar
Burris, R. and Sankappanavar, H., A Course in Universal Algebra, Springer, Berlin, 1981.Google Scholar
Chagrov, A. and Zakharyaschev, M., Modal Logic, Oxford University Press, Oxford, 1997.Google Scholar
Engelking, R., General Topology, second ed., Heldermann Verlag, Berlin, 1989.Google Scholar
Esakia, L., On the theory of modal and superintuitionistic systems, Logical inference, “Nauka”, Moscow, 1979, (In Russian), pp. 147–172.Google Scholar
Esakia, L., Heyting Algebras I. Duality theory, “Metsniereba”, Tbilisi, 1985, (In Russian).Google Scholar
Gabelaia, D., Modal Definability in Topology, Master’s Thesis, University of Amsterdam, 2001.Google Scholar
Gerson, M., The inadequacy of the neighbourhood semantics for modal logic, this Journal, vol. 40 (1975), pp. 141–148.Google Scholar
Gierz, G., Hofmann, K. H., Keimel, K., Lawson, J. D., Mislove, M., and Scott, D. S., Continuous Lattices and Domains, Cambridge University Press, Cambridge, 2003.Google Scholar
Goldblatt, R. I., Metamathematics of modal logic, Reports on Mathematical Logic, (1976), no. 6, pp. 41–77.Google Scholar
Goldblatt, R. I., Diodorean modality in Minkowski space-time, Studia Logica, vol. 39 (1980), no. 2–3, pp. 219–236.Google Scholar
Kremer, P., Strong completeness of S4 for any dense-in-itself metric space. The Review of Symbolic Logic, vol. 6 (2013), no. 3, pp. 545–570.Google Scholar
Kripke, S. A., A completeness theorem in modal logic, this Journal, vol. 24 (1959), pp. 1–14.Google Scholar
Kripke, S. A., Semantical analysis of modal logic. I. Normal modal propositional calculi. Zeitschrift fur mathematische Logik und Grundlagen der Mathematik, vol. 9 (1963), pp. 67–96.Google Scholar
Kuratowski, K. and Mostowski, A., Set Theory, revised edition, North-Holland Publishing Company, Amsterdam, 1976.Google Scholar
Lando, T., Completeness of S4 for the Lebesgue measure algebra. Journal of Philosophical Logic, vol. 41 (2012), no. 2, pp. 287–316.Google Scholar
Lucero-Bryan, J., The d-logic of the real line. Journal of Logic and Computation, vol. 23 (2013), no. 1, pp. 121–156.Google Scholar
McKinsey, J. C. C. and Tarski, A., The algebra of topology. Annals of Mathematics, vol. 45 (1944), pp. 141–191.CrossRefGoogle Scholar
McKinsey, J. C. C. and Tarski, A., On closed elements in closure algebras. Annals of Mathematics, vol. 47 (1946), pp. 122–162.Google Scholar
Pełczyński, A., A remark on spaces 2Χfor zero-dimensional X. Bulletin of the Polish Academy of Sciences, vol. 13 (1965), pp. 85–89.Google Scholar
Rasiowa, H. and Sikorski, R., The Mathematics of Metamathematics, Monografie Matematyczne, Tom 41, Państwowe Wydawnictwo Naukowe, Warsaw, 1963.Google Scholar
Sikorski, R., Boolean Algebras, Springer-Verlag, Berlin, 1960.Google Scholar
Thomason, S. K., Semantic analysis of tense logics, this Journal, vol. 37(1972), pp. 150–158.Google Scholar
Zakharyaschev, M., Wolter, F., and Chagrov, A., Advanced modal logic, Handbook of philosophical logic, vol. 3, Kluwer Academic Publishers, Dordrecht, 2001, pp. 83–266.Google Scholar