Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-30T23:43:32.170Z Has data issue: false hasContentIssue false
  • English
  • Français

Taxonomies of model-theoretically defined topological properties

Published online by Cambridge University Press:  12 March 2014

Paul Bankston
Get access Rights & Permissions [Opens in a new window]

Abstract

A topological classification scheme consists of two ingredients: (1) an abstract class 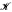of topological spaces; and (2) a “taxonomy”, i.e. a list of first order sentences, together with a way of assigning an abstract class of spaces to each sentence of the list so that logically equivalent sentences are assigned the same class. 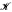is then endowed with an equivalence relation, two spaces belonging to the same equivalence class if and only if they lie in the same classes prescribed by the taxonomy. A space X in 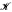is characterized within the classification scheme if whenever Y ∊ 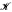and Y is equivalent to X, then Y is homeomorphic to X. As prime example, the closed set taxonomy assigns to each sentence in the first order language of bounded lattices the class of topological spaces whose lattices of closed sets satisfy that sentence. It turns out that every compact two-complex is characterized via this taxonomy in the class of metrizable spaces, but that no infinite discrete space is so characterized. We investigate various natural classification schemes, compare them, and look into the question of which spaces can and cannot be characterized within them.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 55 , Issue 2 , June 1990 , pp. 589 - 603
Copyright
Copyright © Association for Symbolic Logic 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bankston, P., Ultraproducts in topology, General Topology and its Applications, vol. 7 (1977), pp. 289–308.CrossRefGoogle Scholar
[2]Bankston, P., Expressive power in first order topology, this Journal, vol. 49 (1984), pp. 478–487.Google Scholar
[3]Bankston, P., Reduced coproducts of compact Hausdorff spaces, this Journal, vol. 52 (1987), pp. 404–424.Google Scholar
[4]Bankston, P., Co-elementary equivalence for compact Hausdorff spaces and compact abelian groups, Journal of Pure and Applied Algebra (to appear).Google Scholar
[5]Bankston, P., Model-theoretic characterizations of arcs and simple closed curves, Proceedings of the American Mathematical Society, vol. 104 (1988), pp. 898–904.CrossRefGoogle Scholar
[6]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[7]Cherlin, G., Rings of continuous functions: decision problems, Model theory of algebra and arithmetic, Lecture Notes in Mathematics, vol. 834, Springer-Verlag, Berlin, 1980, pp. 44–91.CrossRefGoogle Scholar
[8]Flum, J. and Ziegler, M., Topological model theory, Lecture Notes in Mathematics, vol. 769, Springer-Verlag, Berlin, 1980.CrossRefGoogle Scholar
[9]Gurevič, R., On ultracoproducts of compact Hausdorff spaces, this Journal, vol. 53 (1988), pp. 294–300.Google Scholar
[10]Heinrich, S., Henson, C. W., and Moore, L. C. Jr., A note on elementary equivalence of C(K) spaces, this Journal, vol. 52 (1987), pp. 368–373.Google Scholar
[11]Henson, C. W., Nonstandard hulls of Banach spaces, Israel Journal of Mathematics, vol. 25 (1976), pp. 108–144.CrossRefGoogle Scholar
[12]Henson, C. W.et al., First order topology, Dissertationes Mathematicae/Rozprawy Matematyczne, vol. 143 (1977).Google Scholar
[13]Johnstone, P. T., Stone spaces, Cambridge University Press, Cambridge, 1982.Google Scholar
[14]Kuratowski, K., Topology, Vol. 2, Academic Press, New York, 1968.Google Scholar
[15]Moise, E. E., Geometric topology in dimensions 2 and 3, Springer-Verlag, Berlin, 1977.CrossRefGoogle Scholar
[16]Moore, R. L., Foundations of point set theory, rev. ed., American Mathematical Society, Providence, Rhode Island, 1962.Google Scholar
[17]Shelah, S., The monadic theory of order, Annals of Mathematics, ser. 2, vol. 102 (1975), pp. 379–419.CrossRefGoogle Scholar
[18]Swett, A. K., The first order topology of the real line (unpublished).Google Scholar
[19]Walker, W. C., The Stone-Čech compactification, Springer-Verlag, Berlin, 1974.CrossRefGoogle Scholar
[20]Whyburn, G. T., Analytic topology, American Mathematical Society, Providence, Rhode Island, 1942; corrected reprint, 1971.CrossRefGoogle Scholar
[21]Willard, S., General topology, Addison-Wesley, Reading, Massachusetts, 1970.Google Scholar
[22]Ziegler, M., Topological model theory, Model-theoretic logics (Barwise, J. and Feferman, S., editors), Springer-Verlag, Berlin, 1985, pp. 557–577.Google Scholar