Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T07:41:41.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Successor-invariant first-order logic on finite structures

Published online by Cambridge University Press:  12 March 2014

Benjamin Rossman
Benjamin Rossman*
Affiliation:
Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, Cambridge, MA 02139, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

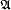We consider successor-invariant first-order logic (FO + succ)inv, consisting of sentences Φ involving an “auxiliary” binary relation S such that (, S1) ⊨ Φ ⇔ (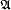, S2) ⊨ Φ for all finite structures 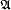and successor relations S1, S2 on 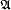. A successor-invariant sentence Φ has a well-defined semantics on finite structures with no given successor relation: one simply evaluates Φ on (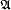, S) for an arbitrary choice of successor relation S. In this article, we prove that (FO + succ)inv is more expressive on finite structures than first-order logic without a successor relation. This extends similar results for order-invariant logic [8] and epsilon-invariant logic [10].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 2 , June 2007 , pp. 601 - 618
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abiteboul, S., Hull, R., and Vianu, V., Foundations of databases, Addison-Wesley, 1995.Google Scholar
[2]Alon, N. and Spencer, J., The probabilistic method, 2nd ed., Wiley, 2000.CrossRefGoogle Scholar
[3]Blass, A. and Gurevich, Y., The logic of choice, this Journal, vol. 65 (2000), pp. 1264–1310.Google Scholar
[4]Blass, A. and Rossman, B., Explicit graphs with extension properties, Bulletin of the European Association for Theoretical Computer Science, (2005), no. 86, pp. 166–175.Google Scholar
[5]Ebbinghaus, H.-D. and Flum, J., Finite model theory, Springer-Verlag, 1996.Google Scholar
[6]Grohe, M. and Schwentick, T., Locality of order-invariant first-order formulas, ACM Transactions on Computational Logic, vol. 1 (2000), pp. 112–130.CrossRefGoogle Scholar
[7]Gurevich, Y., Toward logic tailored for computational complexity. Computation and proof theory (Richter, M.et al., editor), Springer, 1984, pp. 175–216.Google Scholar
[8]Gurevich, Y., Unpublished result.Google Scholar
[9]Libkin, L., Elements of finite model theory, Springer-Verlag, 2004.CrossRefGoogle Scholar
[10]Otto, M., Epsilon-logic is more expressive than first-order logic, this Journal, vol. 65 (2000), pp. 1749–1757.Google Scholar
[11]Rossman, B., Successor-invariance in the finite, Proceedings of the 18th IEEE Symposium of Logic in Computer Science (Kolaitis, Phokion G., editor), 2003, pp. 148–157.Google Scholar