Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T01:02:14.520Z Has data issue: false hasContentIssue false
  • English
  • Français

SQUARES, ASCENT PATHS, AND CHAIN CONDITIONS

Published online by Cambridge University Press:  21 December 2018

CHRIS LAMBIE-HANSON  and
PHILIPP LÜCKE
CHRIS LAMBIE-HANSON
Affiliation:
DEPARTMENT OF MATHEMATICS AND APPLIED MATHEMATICS VIRGINIA COMMONWEALTH UNIVERSITY 1015 FLOYD AVENUE, RICHMOND VIRGINIA 23284, USAE-mail: [email protected]: http://people.vcu.edu/∼cblambiehanso/
PHILIPP LÜCKE
Affiliation:
MATHEMATISCHES INSTITUT UNIVERSITÄT BONN ENDENICHER ALLEE 60, 53115 BONN, GERMANYE-mail: [email protected]: http://www.math.uni-bonn.de/people/pluecke/
Get access Rights & Permissions [Opens in a new window]

Abstract

With the help of various square principles, we obtain results concerning the consistency strength of several statements about trees containing ascent paths, special trees, and strong chain conditions. Building on a result that shows that Todorčević’s principle 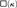$\square \left( {\kappa ,\lambda } \right)$ implies an indexed version of 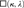$\square \left( {\kappa ,\lambda } \right)$, we show that for all infinite, regular cardinals 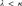$\lambda < \kappa$, the principle 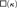$\square \left( \kappa \right)$ implies the existence of a κ-Aronszajn tree containing a λ-ascent path. We then provide a complete picture of the consistency strengths of statements relating the interactions of trees with ascent paths and special trees. As a part of this analysis, we construct a model of set theory in which ${\aleph _2}$-Aronszajn trees exist and all such trees contain ${\aleph _0}$-ascent paths. Finally, we use our techniques to show that the assumption that the κ-Knaster property is countably productive and the assumption that every κ-Knaster partial order is κ-stationarily layered both imply the failure of 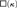$\square \left( \kappa \right)$.

Keywords

Primary 03E05Secondary 03E3503E55square principlesascent pathsspecial treesproductivity of chain conditionsKnaster propertylayered posetswalks on ordinals
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 4 , December 2018 , pp. 1512 - 1538
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baumgartner, J. E., Iterated forcing, Surveys in Set Theory (Mathias, A. R. D., editor), London Mathematical Society Lecture Note Series, vol. 87, Cambridge University Press, Cambridge, 1983, pp. 1–59.Google Scholar
Brodsky, A. M. and Rinot, A., Reduced powers of Souslin trees. Forum of Mathematics, Sigma, vol. 5 (2017), p. e2.CrossRefGoogle Scholar
Cox, S., Layered posets and Kunen’s universal collapse. Notre Dame Journal of Formal Logic, to appear.Google Scholar
Cox, S. and Lücke, P., Characterizing large cardinals in terms of layered posets. Annals of Pure and Applied Logic, vol. 168 (2017), no. 5, pp. 1112–1131.CrossRefGoogle Scholar
Cummings, J., Souslin trees which are hard to specialise. Proceedings of the American Mathematical Society, vol. 125 (1997), no. 8, pp. 2435–2441.CrossRefGoogle Scholar
Cummings, J., Iterated forcing and elementary embeddings, Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 775–883.CrossRefGoogle Scholar
Cummings, J., Foreman, M., and Magidor, M., Squares, scales and stationary reflection. Journal of Mathematical Logic, vol. 1 (2001), no. 1, pp. 35–98.CrossRefGoogle Scholar
Cummings, J. and Schimmerling, E., Indexed squares. Israel Journal of Mathematics, vol. 131 (2002), pp. 61–99.CrossRefGoogle Scholar
Devlin, K. J., Reduced powers of ${\aleph _2}$-trees. Fundamenta Mathematicae, vol. 118 (1983), no. 2, pp. 129–134.CrossRefGoogle Scholar
Hayut, Y. and Lambie-Hanson, C., Simultaneous stationary reflection and square sequences. Journal of Mathematical Logic, vol. 17 (2017), no. 2, p. 1750010, 27.CrossRefGoogle Scholar
Jensen, R. B., The fine structure of the constructible hierarchy. Annals of Mathematical Logic, vol. 4 (1972), pp. 229–308; erratum, ibid. 4 (1972), 443.CrossRefGoogle Scholar
Kunen, K., Saturated ideals, this Journal, vol. 43 (1978), no. 1, pp. 65–76.Google Scholar
Kunen, K., Set Theory: An Introduction to Independence Proofs, Studies in Logic and the Foundations of Mathematics, vol. 102, North-Holland, Amsterdam-New York, 1980.Google Scholar
Lambie-Hanson, C., Squares and covering matrices. Annals of Pure and Applied Logic, vol. 165 (2014), no. 2, pp. 673–694.CrossRefGoogle Scholar
Lambie-Hanson, C., Aronszajn trees, square principles, and stationary reflection. Mathematical Logic Quarterly, vol. 63 (2017), no. 3–4, pp. 265–281.CrossRefGoogle Scholar
Lambie-Hanson, C., Squares and narrow systems, this Journal, vol. 82 (2017), no. 3, pp. 834–859.Google Scholar
Laver, R. and Shelah, S., The ${\aleph _2}$-Souslin hypothesis. Transactions of the American Mathematical Society, vol. 264 (1981), no. 2, pp. 411–417.Google Scholar
Lücke, P., Ascending paths and forcings that specialize higher Aronszajn trees. Fundamenta Mathematicae, vol. 239 (2017), no. 1, pp. 51–84.CrossRefGoogle Scholar
Mitchell, W., Aronszajn trees and the independence of the transfer property. Annals of Mathematical Logic, vol. 5 (1972/73), pp. 21–46.CrossRefGoogle Scholar
Rinot, A., Chain conditions of products, and weakly compact cardinals. Bulletin Symbolic Logic, vol. 20 (2014), no. 3, pp. 293–314.CrossRefGoogle Scholar
Shani, A., Fresh subsets of ultrapowers. Archive for Mathematical Logic, vol. 55 (2016), no. 5–6, pp. 835–845.CrossRefGoogle Scholar
Shelah, S. and Stanley, L., Weakly compact cardinals and nonspecial Aronszajn trees. Proceedings of the American Mathematical Society, vol. 104 (1988), no. 3, pp. 887–897.CrossRefGoogle Scholar
Todorčević, S., Stationary sets, trees and continuums. Publications de l’Institut Mathématique (Beograd) (N.S.), vol. 29 (1981), no. 43, pp. 249–262.Google Scholar
Todorčević, S., Partition relations for partially ordered sets. Acta Mathematica, vol. 155 (1985), no. 1–2, pp. 1–25.CrossRefGoogle Scholar
Todorčević, S., Partitioning pairs of countable ordinals. Acta Mathematica, vol. 159 (1987), no. 3–4, pp. 261–294.CrossRefGoogle Scholar
Todorčević, S., Special square sequences. Proceedings of the American Mathematical Society, vol. 105 (1989), no. 1, pp. 199–205.CrossRefGoogle Scholar
Todorčević, S. and Pérez, V. T., Conjectures of rado and chang and special Aronszajn trees. Mathematical Logic Quarterly, vol. 58 (2012), no. 4–5, pp. 342–347.CrossRefGoogle Scholar