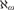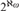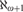Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cummings, James
Džamonja, Mirna
Magidor, Menachem
Morgan, Charles
and
Shelah, Saharon
2017.
A framework for forcing constructions at successors of singular cardinals.
Transactions of the American Mathematical Society,
Vol. 369,
Issue. 10,
p.
7405.