Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T13:55:28.376Z Has data issue: false hasContentIssue false
  • English
  • Français

A small reflection principle for bounded arithmetic

Published online by Cambridge University Press:  12 March 2014

Rineke Verbrugge  and
Albert Visser
Rineke Verbrugge*
Affiliation:
Department of Mathematics and Computer Science, University of Amsterdam, 1018 Tv Amsterdam, The Netherlands
Albert Visser
Affiliation:
Department of Philosophy, University of Gothenburg, S-412 G8 Gothenburg, Sweden, E-mail: [email protected]
*
Department of Philosophy, University of Gothenburg, S-412 G8 Gothenburg, Sweden, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the theory IΔ0+Ω1 and strengthen [Bu86, Theorem 8.6] to the following: if NP ≠ co-NP, then Σ-completeness for witness comparison foumulas is not provable in bounded arithmetic. i.e.,

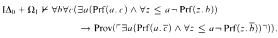
Next we study a “small reflection principle” in bounded arithmetic. We prove that for all sentences φ

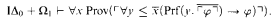
The proof hinges on the use of definable cuts and partial satisfaction predicates akin to those introduced by Pudlák in [Pu86].

Finally, we give some applications of the small reflection principle, showing that the principle can sometimes be invoked in order to circumvent the use of provable Σ-completeness for witness comparison formulas.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 3 , September 1994 , pp. 785 - 812
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Ad90]Adamowicz, Z., End-extending models of IΔ0 + EXP + BΣ1, Fundamenta Mathematicae, vol. 136 (1990), pp. 133–145.CrossRefGoogle Scholar
[Ad93]Adamowicz, Z., A contribution to the end-extension problem and the ∏1 conservativeness problem, Annals of Pure and Applied Logic, vol. 61 (1993). pp. 3–48.CrossRefGoogle Scholar
[BDG87]Balcázar, J. L., Díaz, J., and Gabarró, J.. Structural complexity I, Springer-Verlag, Berlin, 1987.Google Scholar
[Be89]Beklemishev, L. D., On the classification of propositional provability logics, Mathematics of the USSR Izvestiya, vol. 35 (1990), pp. 247–275.CrossRefGoogle Scholar
[Be91]Beklemishev, L. D., On bimodal provability logics for ∏1-axiomatized extensions of arithmetical theories, ITLI prepublication series, X-91-09, University of Amsterdam, Amsterdam, 1991.Google Scholar
[BV93]Berarducci, A. and Verbrugge, L. C., On the provability logic of bounded arithmetic, Annals of Pure and Applied Logic, vol. 61 (1993), pp. 75–93.CrossRefGoogle Scholar
[Bu86]Buss, S., Bounded arithmetic, Bibliopolis, Napoli, 1986.Google Scholar
[Fe60]Feferman, S., Arithmetization of metamathematics in a general setting, Fundamenta Mathematicae, vol. 49 (1960), pp. 35–92.CrossRefGoogle Scholar
[FR79]Ferrante, J. and Rackoff, C. W., The computational complexity of logical theories, Springer-Verlag, Berlin, 1979.CrossRefGoogle Scholar
[GS79]Guaspari, D. and Solovay, R. M., Rosser sentences, Annals of Mathematical Logic, vol. 16 (1979). pp. 81–99.CrossRefGoogle Scholar
[Há83]Hájek, P., On a new notion of partial conservativity, Logic colloquium ‘83 (Börger, E.et al. editors), vol. 2, Springer–Verlag, Berlin, 1983, pp. 217–232.Google Scholar
[HP93]Hájek, P. and Pudlák, P., Metamathematics of first-order arithmetic, Springer-Verlag, Berlin, 1993.CrossRefGoogle Scholar
[Jo87]de Jongh, D. H. J., A simplification of a completeness proof of Guaspari and Solovay, Studia Logica, vol. 46 (1987). pp. 187–192.CrossRefGoogle Scholar
[JM87]de Jongh, D. H. J. and Montagna, F., Generic generalized Rosser fixed points, Studia Logica, vol. 46 (1987), pp. 193–203.CrossRefGoogle Scholar
[JV88]de Jongh, D. H. J. and Veltman, F., Intensional logic, lecture notes, Philosophy Department, University of Amsterdam, Amsterdam, 1988.Google Scholar
[JMM91]de Jongh, D. H. J., Jumelet, M., and Montagna, F., On the proof of Solovay's theorem, Studia Logica, vol. 50 (1991), pp. 51–70.CrossRefGoogle Scholar
[JM91]de Jongh, D. H. J. and Montagna, F., Rosser orderings and free variables, Studia Logica, vol. 50 (1991), pp. 71–80.CrossRefGoogle Scholar
[KH82]Kent, C. F. and Hodgson, B. R., An arithmetical characterization of NP, Theoretical Computer Science, vol. 21 (1982). pp. 255–267.CrossRefGoogle Scholar
[KP89]Krajíček, J. and Pudlák, P., On the structure of initial segments of models of arithmetic, Archives of Mathematical Logic, vol. 28 (1989). pp. 91–98.CrossRefGoogle Scholar
[MA78]Manders, K. and Adleman, L., NP-complete decision problems for binary quadratics, Journal of Computer and System Sciences, vol. 16 (1978), pp. 168–184.CrossRefGoogle Scholar
[Ne86]Nelson, E., Predicative arithmetic, Mathematical Notes 32, Princeton University Press, Princeton, New Jersey, 1986.CrossRefGoogle Scholar
[Pa71]Parikh, R., Existence and feasibility in arithmetic, this Journal, vol. 36 (1971), pp. 494–508.Google Scholar
[Pu83]Pudlák, P., A definition of exponentiation by a bounded arithmetical formula, Commentationes Mathematicae Universitatis Carolinae, vol. 24 (1983). pp. 667–671.Google Scholar
[Pu85]Pudlák, P., Cuts, consistency statements and interpretations, this Journal, vol. 50 (1985), pp. 423–441.Google Scholar
[Pu86]Pudlák, P., On the length of proofs of finitistic consistency statements in first order theories, Logic colloquium ’84 (Paris, J. B.et al., editors), North-Holland, Amsterdam, 1986, pp. 165–196.Google Scholar
[Pu87]Pudlák, P., Improved bounds to the length of proofs of finitistic consistency statements, Logic and combinatorics (Simpson, S. G., editor): Contemporary Mathematics, vol. 35. American Mathematical Society, Providence, Rhode Island, 1987, pp. 309–332.Google Scholar
[Sm85]Smoryński, C., Self-reference and modal logic, Springer–Verlag, New York, 1985.CrossRefGoogle Scholar
[So76]Solovay, R. M., Provability interpretations of modal logic, Israel Journal of Mathematics, vol. 25 (1976), pp. 287–304.CrossRefGoogle Scholar
[So76b]Solovay, R. M., On interpretability in set theories, manuscript, 1976.Google Scholar
[So89]Solovay, R. M., Injecting inconsistencies into models of PA, Annals of Pure and Applied Logic, vol. 44 (1989), pp. 261–302.CrossRefGoogle Scholar
[St76]Stockmeyer, L. J., The polynomial-time hierarchy, Theoretical Computer Science, vol. 3 (1976), pp. 1–22.CrossRefGoogle Scholar
[Šv83]Švejdar, V., Modal analysis of generalized Rosser sentences, this Journal, vol. 48 (1983), pp. 986–999.Google Scholar
[Ta75]Takeuti, G., Proof theory, North-Holland, Amsterdam, 1975.Google Scholar
[Ta88]Takeuti, G., Bounded arithmetic and truth definition, Annals of Pure and Applied Logic, vol. 39 (1988). pp. 75–104.CrossRefGoogle Scholar
[Ve88]Verbrugge, L. C., Does Solovay's completeness theorem extend to bounded arithmetic?, Master's Thesis, University of Amsterdam, Amsterdam, 1988.Google Scholar
[Ve89]Verbrugge, L. C., Σ-completeness and bounded arithmetic, ITLI prepublication series for mathematical logic and foundations, ML-89-05, University of Amsterdam, Amsterdam, 1989.Google Scholar
[Vi81]Visser, A., Aspects of diagonalization & provability, Ph.D. thesis, University of Utrecht, Utrecht, 1981.Google Scholar
[Vi82]Visser, A., On the completeness principle, Annals of Mathematical Logic, vol. 22 (1982), pp. 263–295.Google Scholar
[Vi85]Visser, A., Evaluation, provably deductive equivalence in Heyting's Arithmetic of substitution instances of propositional formulas, Logic Group Prepint Series, no. 4, University of Utrecht, Utrecht, 1985.Google Scholar
[Vi90]Visser, A., Interpretabilty logic, Mathematical logic (Petkov, P. P., editor), Proceedings of the Heyting ’88 summer school. Plenum Press, New York, 1990, pp. 175–209.Google Scholar
[Vi91]Visser, A., The formalization of interpretability, Studia Logica, vol. 50 (1991), pp. 81–105.CrossRefGoogle Scholar
[WP87]Wilkie, A. J. and Paris, J. B., On the scheme of induction for bounded arithmetic formulas, Annals of Pure and Applied Logic, vol. 35 (1987), pp. 261–302.CrossRefGoogle Scholar
[WP89]Wilkie, A. J. and Paris, J. B., On the existence of end extensions of models of bounded induction, Logic, methodology and philosophy of science VIII (Fenstad, J. E.et al, editors), North-Holland, Amsterdam, 1989, pp. 143–161.Google Scholar
[Wr76]Wrathall, C., Complete sets and the polynomial time hierarchy, Theoretical Computer Science vol. 3 (1976). pp. 23–33.CrossRefGoogle Scholar