Hostname: page-component-f554764f5-rj9fg Total loading time: 0 Render date: 2025-04-21T01:18:05.669Z Has data issue: false hasContentIssue false
  • English
  • Français

THE SHAPE OF COMPACT COVERS

Part of: Topological and differentiable algebraic systems Set theory Connections with other structures, applications Ordered sets Spaces with richer structures Fairly general properties

Published online by Cambridge University Press:  29 October 2024

ZIQIN FENG  and
PAUL GARTSIDE
ZIQIN FENG*
Affiliation:
DEPARTMENT OF MATHEMATICS AND STATISTICS AUBURN UNIVERSITY AUBURN, AL 36849 USA
PAUL GARTSIDE
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF PITTSBURGH PITTSBURGH, PA 15260 USA E-mail: [email protected]
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a space X let 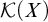$\mathcal {K}(X)$ be the set of compact subsets of X ordered by inclusion. A map 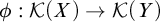$\phi :\mathcal {K}(X) \to \mathcal {K}(Y)$ is a relative Tukey quotient if it carries compact covers to compact covers. When there is such a Tukey quotient write 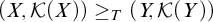$(X,\mathcal {K}(X)) \ge _T (Y,\mathcal {K}(Y))$, and write 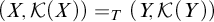$(X,\mathcal {K}(X)) =_T (Y,\mathcal {K}(Y))$ if 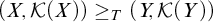$(X,\mathcal {K}(X)) \ge _T (Y,\mathcal {K}(Y))$ and vice versa.

We investigate the initial structure of pairs 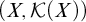$(X,\mathcal {K}(X))$ under the relative Tukey order, focussing on the case of separable metrizable spaces. Connections are made to Menger spaces.

Applications are given demonstrating the diversity of free topological groups, and related free objects, over separable metrizable spaces. It is shown a topological group G has the countable chain condition if it is either $\sigma $-pseudocompact or for some separable metrizable M, we have 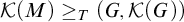$\mathcal {K}(M) \ge _T (G,\mathcal {K}(G))$.

Keywords

Tukey ordercompact coversseparable metrizable space

MSC classification

Primary: 03E04: Ordered sets and their cofinalities; pcf theory 06A07: Combinatorics of partially ordered sets 22A05: Structure of general topological groups 54D30: Compactness 54D45: Local compactness, $sigma$-compactness
Secondary: 54E35: Metric spaces, metrizability 54H11: Topological groups
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 15
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arhangel’skií, A. and Tkachenko, M., Topological Groups and Related Structures , Atlantis Press and World Scientific, Paris, 2008.CrossRefGoogle Scholar
Aurichi, L., D-spaces, topological games, and selection principles . Topology Proceedings , vol. 36 (2010), pp. 107–122.Google Scholar
Bartoszyński, T. and Shelah, S., Continuous images of sets of reals . Topology and its Applications , vol. 116 (2001), pp. 243–253.CrossRefGoogle Scholar
Bartoszyński, T. and Tsaban, B., Hereditary topological diagonalizations and the Menger–Hurewicz conjectures . Proceedings of the American Mathematical Society , vol. 134 (2006), pp. 605–615.CrossRefGoogle Scholar
Cascales, B. and Orihuela, J., A biased view of topology as a tool in functional analysis , Recent Progress in General Topology III (K.P. Hart, J. van Mill, and P. Simon, editors), Atlantis Press, Paris, 2014, pp. 93–164.CrossRefGoogle Scholar
Cascales, B., Orihuela, J., and Tkachuk, V., Domination by second countable spaces and Lindelöf $\varSigma$ property . Topology and its Applications , vol. 158 (2011), pp. 204–214.CrossRefGoogle Scholar
Engelking, R., General Topology , Heldermann Verlag, 1989.Google Scholar
Gartside, P., Tukey order and diversity of free abelian topological groups . Journal of Pure and Applied Algebra , vol. 225 (2021), no. 10, p. 106712.CrossRefGoogle Scholar
Gartside, P. and Mamatelashvili, A., Tukey order on compact subsets of separable metric spaces . Journal of Symbolic Logic , vol. 81 (2016), no. 1, pp. 181–200.CrossRefGoogle Scholar
Gartside, P. and Mamatelashvili, A., Tukey order, calibres and the rationals . Annals of Pure and Applied Logic , vol. 172 (2021), no. 1, p. 102873.CrossRefGoogle Scholar
Gartside, P., Medini, A., and Zdomskyy, L., private communication.Google Scholar
Gartside, P., Reznichenko, E., and Sipacheva, O., Maltsev and retral spaces . Topology and its Applications , vol. 80 (1997), pp. 115–129.CrossRefGoogle Scholar
Just, W., Miller, A., Scheepers, M., and Szeptycki, P., The combinatorics of open covers II . Topology and its Applications , vol. 73 (1996), pp. 241–266.CrossRefGoogle Scholar
Just, W. and Wicke, H., Some conditions under which tri-quotient or compact-covering maps are inductively perfect . Topology and its Applications , vol. 55 (1994), no. 3, pp. 289–305.CrossRefGoogle Scholar
Reznichenko, E. and Uspenskij, V., Pseudocompact Mal’tsev spaces . Topology and its Applications , vol. 86 (1998), pp. 83–104.CrossRefGoogle Scholar
Tkachenko, M., On the Souslin property in free topological groups over compact Hausdorff spaces . Mathematical Notes , vol. 34 (1983), pp. 790–793.CrossRefGoogle Scholar
Tukey, J., Convergence and Uniformity in Topology , Annals of Mathematics Studies, 2, Princeton University Press, Princeton, 1940.Google Scholar
Uspenskii, V., Topological groups generated by a Lindelöf $\varSigma$ -space has the Souslin property . Soviet Mathematics – Doklady , vol. 26 (1982), pp. 166–169.Google Scholar