Article contents
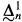 sets of reals
sets of reals
Published online by Cambridge University Press: 12 March 2014
Extract
Some of the most striking results in modern set theory have emerged from the study of simply-definable sets of real numbers. Indeed, simple questions like: what are the posible cardinalities?, are they measurable?, do they have the property of Baire?, etc., cannot be answered in ZFC.
When one restricts the attention to the analytic sets, i.e., the continuous images of Borel sets, then ZFC does provide an answer to these questions. But this is no longer true for the projective sets, i.e., all the sets of reals that can be obtained from the Borel sets by taking continuous images and complements. In this paper we shall concentrate on particular projective classes, the 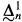 , and using forcing constructions we will produce models of ZFC where, for some n, all
, and using forcing constructions we will produce models of ZFC where, for some n, all 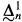 , sets have some specified property. For the definition and basic facts about the projective classes
, sets have some specified property. For the definition and basic facts about the projective classes 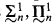 , and
, and 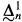 , as well as the Kleene (or lightface) classes
, as well as the Kleene (or lightface) classes 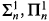 , and
, and 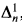 , we refer the reader to Moschovakis [19].
, we refer the reader to Moschovakis [19].
The first part of the paper is about measure and category. Early in this century, Luzin [16] and Luzin-Sierpiński [17] showed that all analytic (i.e., 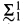 ) sets of reals are Lebesgue measurable and have the property of Baire.
) sets of reals are Lebesgue measurable and have the property of Baire.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1997
References
REFERENCES
- 10
- Cited by


