Article contents
Replacement and collection in intuitionistic set theory
Published online by Cambridge University Press: 12 March 2014
Extract
Intuitionistic Zermelo-Fraenkel set theory, which we call ZFI, was introduced by Friedman and Myhill in [3] in 1970. The idea was to have a theory with the same axioms as ordinary classical ZF, but with Heyting's predicate calculus HPC as the underlying logic. Since some classically equivalent statements are intuitionistically inequivalent, however, it was not always obvious which form of a classical axiom to take. For example, the usual formulation of the axiom of foundation had to be replaced with a principle of transfinite induction on the membership relation in order to avoid having excluded middle provable and thus making the logic classical. In [3] the replacement axiom is taken in its most common classical form:
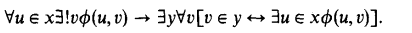
In the presence of the separation axiom,
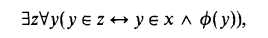
this is equivalent to the axiom
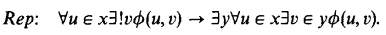
It is this schema Rep that we shall call the replacement axiom.
Friedman and Myhill were able to show in [3] that ZFI has a number of desirable “constructive” properties, including the existence property for both numbers and sets. They were not able to determine, however, whether ZFI is proof-theoretically as strong as ZF. This is still open.
Three years later, in [2], Friedman introduced a theory ZF− which is like ZFI except that the replacement axiom is changed to the classically equivalent collection axiom:
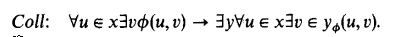
He showed that ZF− is proof-theoretically of the same strength as ZF, and he asked whether ZF− is equivalent to ZFI.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1985
References
REFERENCES
A correction has been issued for this article:
- 2
- Cited by
Linked content
Please note a has been issued for this article.


