Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-30T20:18:49.183Z Has data issue: false hasContentIssue false
  • English
  • Français

Pseudo-complements and ordinal logics based on consistency statements

Published online by Cambridge University Press:  12 March 2014

Robert A. Di Paola
Robert A. Di Paola*
Affiliation:
University of California, Los Angeles
Get access Rights & Permissions [Opens in a new window]

Extract

Following [1] we write {n} for the nth recursively enumerable (re) set; that is, {n} = {x|VyT(n, x, y)}. By a “pair (T, α)” we mean a consistent re extension T of Peano arithmetic P and an RE-formula α which numerates the non-logical axioms of T in P [4]. Given a pair (T, α) and a particular formula 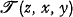which binumerates the Kleene T predicate in P, there can be defined a primitive recursive function Nα such that 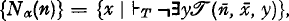and which has the additional property that {Nα(Nα(n))} = ø for all n.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 31 , Issue 3 , 02 September 1966 , pp. 359 - 364
Copyright
Copyright © Association for Symbolic Logic 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Davis, Martin, Computability and unsolvability, McGraw-Hill, 1958.Google Scholar
[2]Martin|Davis, Pseudo-complements of recursively enumerable sets, (Preliminary report), Bulletin of the American Mathematical Society, vol. 60 (1954), pp. 169–170.Google Scholar
[3]Di Paola, Robert A., Some properties of pseudo-complements of recursively enumerable sets. To appear.Google Scholar
[4]Feferman, S., Arithmetization of metamathematics in a general setting, Fundamenta mathematicae, vol. 49 (1960), pp. 35–92.CrossRefGoogle Scholar
[5]Feferman, S., Transfinite recursive progression of axiomatic theories, this Journal, vol. 27 (1962), pp. 259–316.Google Scholar
[6]Friedberg, Richard, Two recursively enumerable sets of incomparable degrees of unsolvability, Proceedings of the National Academy of Science, vol. 43 (1957), pp. 236–238.CrossRefGoogle ScholarPubMed
[7]Turing, A. M., Systems of logic based on ordinals, Proceedings of the London Mathematical Society, vol. 45 (1939), pp. 161–228.CrossRefGoogle Scholar