Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T08:05:50.576Z Has data issue: false hasContentIssue false
  • English
  • Français

PREDICATIVE COLLAPSING PRINCIPLES

Published online by Cambridge University Press:  09 December 2019

ANTON FREUND
ANTON FREUND*
Affiliation:
FACHBEREICH MATHEMATIK TECHNISCHE UNIVERSITÄT DARMSTADT DARMSTADT, GERMANY E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that arithmetical transfinite recursion is equivalent to a suitable formalization of the following: For every ordinal α there exists an ordinal β such that 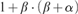$1 + \beta \cdot \left( {\beta + \alpha } \right)$ (ordinal arithmetic) admits an almost order preserving collapse into β. Arithmetical comprehension is equivalent to a statement of the same form, with 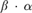$\beta \cdot \alpha$ at the place of 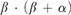$\beta \cdot \left( {\beta + \alpha } \right)$. We will also characterize the principles that any set is contained in a countable coded ω-model of arithmetical transfinite recursion and arithmetical comprehension, respectively.

Keywords

03B3003F1503F35reverse mathematicswell-ordering principlesBachmann–Howard fixed pointsdilatorsVeblen functionarithmetical transfinite recursionarithmetical comprehension
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 1 , March 2020 , pp. 511 - 530
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aczel, P., Mathematical problems in logic, Ph.D. thesis, Oxford, 1966.Google Scholar
Aczel, P., Normal functors on linear orderings, this Journal, vol. 32 (1967), p. 430, abstract to a paper presented at the annual meeting of the Association for Symbolic Logic, Houston, Texas, 1967.Google Scholar
Afshari, B. and Rathjen, M., Reverse mathematics and well-ordering principles: A pilot study. Annals of Pure and Applied Logic, vol. 160 (2009), pp. 231–237.CrossRefGoogle Scholar
Buchholz, W., A survey on ordinal notations around the Bachmann-Howard ordinal, Feferman on Foundations (Jäger, G. and Sieg, W., editors), Springer, Cham, 2017, pp. 71–100.Google Scholar
Freund, A., Type-two well-ordering principles, admissible sets, and ${\rm{\Pi }}_1^1$-comprehension, Ph. D. thesis, University of Leeds, 2018. Available at http://etheses.whiterose.ac.uk/20929/.Google Scholar
Freund, A., .${\rm{\Pi }}_1^1$-comprehension as a well-ordering principle. Advances in Mathematics, vol. 355 (2019). doi:10.1016/j.aim.2019.106767.CrossRefGoogle Scholar
Freund, A., A categorical construction of Bachmann-Howard fixed points. Bulletin of the London Mathematical Society, vol. 51 (2019), no. 5, pp. 801–814.CrossRefGoogle Scholar
Freund, A., Computable aspects of the Bachmann-Howard principle. Journal of Mathematical Logic, in press. doi:10.1142/S0219061320500063.Google Scholar
Freund, A., How strong are single fixed points of normal functions?, 2019, p. Preprint available as arXiv:1906.00645.Google Scholar
Freund, A. and Rathjen, M., Derivatives of normal functions in reverse mathematics, 2019, p. Preprint available as arXiv:1904.04630.Google Scholar
Girard, J.-Y., .${\rm{\Pi }}_2^1$-logic, part 1: Dilators. Annals of Pure and Applied Logic, vol. 21 (1981), pp. 75–219.Google Scholar
Girard, J.-Y., Proof Theory and Logical Complexity, vol. 1, Studies in Proof Theory, Bibliopolis, Napoli, 1987.Google Scholar
Hirst, J. L., Reverse mathematics and ordinal exponentiation,. Annals of Pure and Applied Logic, vol. 66 (1994), pp. 1–18.CrossRefGoogle Scholar
Marcone, A. and Montalbán, A., The Veblen functions for computability theorists, this Journal, vol. 76 (2011), pp. 575–602.Google Scholar
Rathjen, M., ω-models and well-ordering principles, Foundational Adventures: Essays in Honor of Harvey M. Friedman (Tennant, N., editor), College Publications, London, 2014, pp. 179–212.Google Scholar
Rathjen, M. and Valencia Vizcaíno, P. F., Well ordering principles and bar induction, Gentzen’s Centenary: The Quest for Consistency (Kahle, R. and Rathjen, M., editors), Springer, Berlin, 2015, pp. 533–561.CrossRefGoogle Scholar
Rathjen, M. and Weiermann, A., Proof-theoretic investigations on Kruskal’s theorem. Annals of Pure and Applied Logic, vol. 60 (1993), pp. 49–88.CrossRefGoogle Scholar
Rathjen, M. and Weiermann, A., Reverse mathematics and well-ordering principles, Computability in Context: Computation and Logic in the Real World (Cooper, S. B. and Sorbi, A., editors), Imperial College Press, London, 2011, pp. 351–370.CrossRefGoogle Scholar
Schütte, Kurt., Proof Theory, Grundlehren der Mathematischen Wissenschaften, vol. 225, Springer, Berlin, 1977.CrossRefGoogle Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, Perspectives in Logic, Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Sommer, R., Transfinite induction within Peano arithmetic,. Annals of Pure and Applied Logic, vol. 76 (1995), pp. 231–289.CrossRefGoogle Scholar