Article contents
Predicate functors revisited
Published online by Cambridge University Press: 12 March 2014
Extract
Quantification theory, or first-order predicate logic, can be formulated in terms purely of predicate letters and a few predicate functors which attach to predicates to form further predicates. Apart from the predicate letters, which are schematic, there are no variables. On this score the plan is reminiscent of the combinatory logic of Schönfinkel and Curry. Theirs, however, had the whole of higher set theory as its domain; the present scheme stays within the bounds of predicate logic.
In 1960 I published an apparatus to this effect, and an improved version in 1971. In both versions I assumed two inversion functors, major and minor; also a cropping functor and the obvious complement functor. The effects of these functors, when applied to an n-place predicate, are as follows:
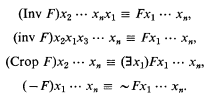
The variables here are explanatory only and no part of the final notation. Ultimately the predicate letters need exponents showing the number of places, but I omit them in these pages.
A further functor-to continue now with the 1971 version-was padding:
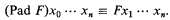
Finally there was a zero-place predicate functor, which is to say simply a constant predicate, namely the predicate ‘I’ of identity, and there was a two-place predicate functor ‘∩’ of intersection. The intersection ‘F ∩ G’ received a generalized interpretation, allowing ‘F’ and ‘G’ to be predicates with unlike numbers of places. However, Steven T. Kuhn has lately shown me that the generalization is unnecessary and reducible to the homogeneous case.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1981
References
REFERENCES
- 12
- Cited by


