Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bürger, Gerd
1989.
TheL <ω-theory of the class of Archimedian real closed fields.
Archive for Mathematical Logic,
Vol. 28,
Issue. 3,
p.
155.
Koepke, Peter
1989.
On the elimination of Malitz quantifiers over Archimedian real closed fields.
Archive for Mathematical Logic,
Vol. 28,
Issue. 3,
p.
167.
Kreinovich, Vladik
and
Kosheleva, Olga
1994.
An Application of Logic to Combinatorial Geometry: How Many Tetrahedra are Equidecomposable with a Cube?.
Mathematical Logic Quarterly,
Vol. 40,
Issue. 1,
p.
31.
Lenski, Wolfgang
1995.
Quantifiers: Logics, Models and Computation.
p.
139.
Ebbinghaus, Heinz-Dieter
1995.
Quantifiers: Logics, Models and Computation.
p.
25.


 -theory of ℜ is decidable, where
-theory of ℜ is decidable, where 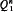 denotes the Malitz quantifier of order
denotes the Malitz quantifier of order 