Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T20:57:13.920Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE INTERPLAY BETWEEN EFFECTIVE NOTIONS OF RANDOMNESS AND GENERICITY

Published online by Cambridge University Press:  30 January 2019

LAURENT BIENVENU  and
CHRISTOPHER P. PORTER
LAURENT BIENVENU
Affiliation:
LABRI, CNRS & UNIVERSITÉ DE BORDEAUX TALENCE, FRANCEE-mail: [email protected]
CHRISTOPHER P. PORTER
Affiliation:
DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE DRAKE UNIVERSITY DES MOINES, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the power and limitations of computing effectively generic sequences using effectively random oracles. Previously, it was known that every 2-random sequence computes a 1-generic sequence (as shown by Kautz) and every 2-random sequence forms a minimal pair in the Turing degrees with every 2-generic sequence (as shown by Nies, Stephan, and Terwijn). We strengthen these results by showing that every Demuth random sequence computes a 1-generic sequence and that every Demuth random sequence forms a minimal pair with every pb-generic sequence (where pb-genericity is an effective notion of genericity that is strictly between 1-genericity and 2-genericity). Moreover, we prove that for every comeager 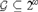${\cal G} \subseteq {2^\omega }$, there is some weakly 2-random sequence X that computes some 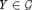$Y \in {\cal G}$, a result that allows us to provide a fairly complete classification as to how various notions of effective randomness interact in the Turing degrees with various notions of effective genericity.

Keywords

03D2803D32algorithmic randomnesseffective genericity
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 1 , March 2019 , pp. 393 - 407
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andrews, U., Gerdes, P., and Miller, J. S., The degrees of bi-hyperhyperimmune sets. Annals of Pure and Applied Logic, vol. 165 (2014), no. 3, pp. 803–811.10.1016/j.apal.2013.10.004CrossRefGoogle Scholar
Barmpalias, G., Day, A., and Lewis-Pye, A., The typical Turing degree. Proceedings of the London Mathematical Society, vol. 109 (2013), no. 1, pp. 1–39.10.1112/plms/pdt065CrossRefGoogle Scholar
Barmpalias, G., Downey, R., and Ng, K. M., Jump inversions inside effectively closed sets and applications to randomness, this Journal, vol. 76 (2011), no. 2, pp. 491–518.Google Scholar
Bienvenu, L., Downey, R., Greenberg, N., Nies, A., and Turetsky, D., Characterizing lowness for Demuth randomness, this Journal, vol. 79 (2014), no. 2, pp. 526–560.Google Scholar
Bienvenu, L. and Patey, L., Diagonally non-computable functions and fireworks. Information and Computation, vol. 253 (2017), pp. 64–77.10.1016/j.ic.2016.12.008CrossRefGoogle Scholar
Demuth, O., On some classes of arithmetical real numbers. Commentationes Mathematicae Universitatis Carolinae, vol. 23 (1982), pp. 453–465.Google Scholar
Demuth, O., Remarks on the structure of tt-degrees based on constructive measure theory. Commentationes Mathematicae Universitatis Carolinae, vol. 29 (1988), no. 2, pp. 233–247.Google Scholar
Downey, R. and Hirschfeldt, D., Algorithmic Randomness and Complexity, Theory and Applications of Computability, Springer-Verlag, New York, 2010.10.1007/978-0-387-68441-3CrossRefGoogle Scholar
Downey, R., Jockusch, C., and Stob, M., Array nonrecursive degrees and genericity, Computability, Enumerability, Unsolvability. Directions in Recursion Theory (Cooper, S. B., Slaman, T. A., and Wainer, S. S., editors), London Mathematical Society Lecture Notes Series, Cambridge University Press, Cambridge, 1996, pp. 93–104.10.1017/CBO9780511629167.005CrossRefGoogle Scholar
Downey, R. and Ng, K. M., Lowness for Demuth randomness, Conference on Computability in Europe (CiE 2009), Lecture Notes in Computer Science, vol. 5635, Springer-Verlag, Berlin, 2009, pp. 154–166.Google Scholar
Franklin, J. N. Y. and Ng, K. M., Difference randomness. Proceedings of the American Mathematical Society, vol. 139 (2011), pp. 345–360.10.1090/S0002-9939-2010-10513-0CrossRefGoogle Scholar
Franklin, J. N. Y. and Ng, K. M., ω-change randomness and weak Demuth randomness, this Journal, vol. 79 (2014), no. 3, pp. 776–791.Google Scholar
Greenberg, N. and Turetsky, D., Strong jump-traceability and Demuth randomness. Proceedings of the London Mathematical Society, vol. 108 (2014), pp. 738–779.10.1112/plms/pdt040CrossRefGoogle Scholar
Kautz, S. M., Degrees of random sequences, Ph.D. thesis, Cornell University, 1991.Google Scholar
Kučera, A., Measure, ${\rm{\Pi }}_1^0$ classes, and complete extensions of PA. Lecture Notes in Mathematics, vol. 1141 (1985), pp. 245–259.10.1007/BFb0076224CrossRefGoogle Scholar
Kucera, A. and Nies, A., Demuth randomness and computational complexity. Annals of Pure and Applied Logic, vol. 162 (2011), no. 7, pp. 504–513.10.1016/j.apal.2011.01.004CrossRefGoogle Scholar
Kurtz, S., Randomness and Genericity in the Degrees of Unsolvability, Ph.D. dissertation, University of Illinois at Urbana, 1981.Google Scholar
Nies, A., Computability and Randomness, Oxford Logic Guides, Oxford University Press, Oxford, 2009.10.1093/acprof:oso/9780199230761.001.0001CrossRefGoogle Scholar
Nies, A., Stephan, F., and Terwijn, S., Randomness, relativization and Turing degrees, this Journal, vol. 70 (2005), pp. 515–535.Google Scholar
Rumyantsev, A. Y. and Shen, A., Probabilistic constructions of computable objects and a computable version of Lovász local lemma. Fundamenta Informaticae, vol. 132 (2014), no. 1, pp. 1–14.Google Scholar
Yates, C. E. M., Initial segments of the degrees of unsolvability part II: Minimal degrees, this Journal, vol. 35 (1970), no. 2, pp. 243–266.Google Scholar